Science:Math Exam Resources/Courses/MATH105/April 2013/Question 05 (a)

MATH105 April 2013

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q1 (l)  •  Q1 (m)  •  Q1 (n)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q3 (a)  •  Q3 (b)  •  Q4 (a)  •  Q4 (b)  •  Q5 (a)  •  Q5 (b)  •  Q6 (a)  •  Q6 (b)  •  

   Other MATH105 Exams

  •  April 2009  •  April 2011  •  April 2010  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2017  •  April 2018  •  

Question 05 (a)

A study conducted at a waste disposal site reveals soil contamination over a region that can be described as the interior of the circle $\displaystyle x^{2}+y^{2}=16$ where x and y are in miles. In order to build a circular enclosure to contain all polluted territory, the manager of the site wants to find the radius of the smallest circle centered at (2, 2) that contains the entire contamination region. Formulate this as a constrained optimization problem, clearly stating the objective function and the constraint. Note that you do not need to do any computation in part (a).

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
We with to make the radius of the new circle around (2,2) as small as possible and as large as necessary to contain all points from the first circle around (0,0).

Hint 2
Given any point (x,y), what is the distance from that point to the centre of our new cirle (2,2)?

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

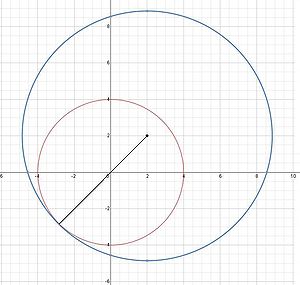
Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Examine the picture below The red circle describes the contaminated region. Our blue circle has to be just large enough to completely contain the red circle. Hence, we need to find the distance between any point on the red circle and the centre of the blue circle, (2,2). The radius of the blue circle is then the smallest number that is bigger than all these distances. The distance between any point (x,y) and (2,2) is given by $\displaystyle {\sqrt {(x-2)^{2}+(y-2)^{2}}}$. Hence, the radius r we are looking for is the maximum value of distances from points on the red circle to the centre of the blue circle: $\displaystyle r={\sqrt {(x-2)^{2}+(y-2)^{2}}}$ subject to this point $(x,y)$ lying on the red circle $\displaystyle x^{2}+y^{2}=16$ Maximizing this distance gives the smallest possible radius such that the blue circle still encloses the entire contamination area.

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Optimization, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag