Science:Math Exam Resources/Courses/MATH105/April 2010/Question 03

{{#incat:MER QGQ flag|{{#incat:MER QGH flag|{{#incat:MER QGS flag|}}}}}}

MATH105 April 2010

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q1 (l)  •  Q1 (m)  •  Q1 (n)  •  Q2  •  Q3  •  Q4  •  Q5 (a)  •  Q5 (b)  •  Q5 (c)  •  Q6  •  

   Other MATH105 Exams

  •  April 2009  •  April 2011  •  April 2010  •  April 2012  •  April 2013  •  April 2014  •  April 2015  •  April 2016  •  April 2017  •  April 2018  •  

Question 03
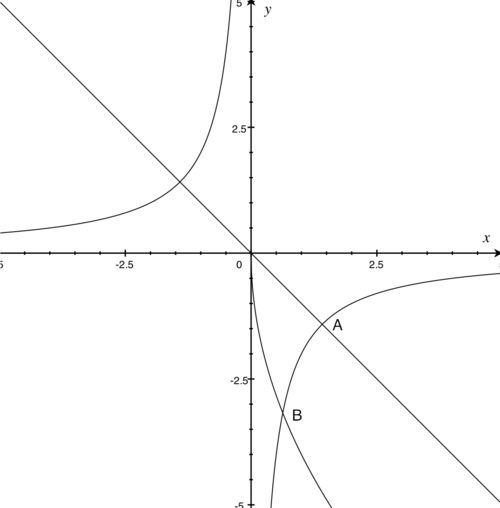
Find the area of the region bounded by $y=-{\frac {2}{x}},\quad y=-4{\sqrt {x}}\quad {\text{and}}\quad y=-x.$

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
What does this region look like? How can you find the area of such a region?

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

First, we sketch each of the three curves to see what is the region that we are talking about. We will need to find the coordinates of points A and B which are the intersection of curves. For A we have ${\begin{aligned}-x&=-{\frac {2}{x}}\\x^{2}&=2\\x&=\pm {\sqrt {2}}\end{aligned}}$ We can see from the picture that we are interested in the point with a positive x coordinate, so $\displaystyle A=({\sqrt {2}},-{\sqrt {2}})$ For B we have ${\begin{aligned}-4{\sqrt {x}}&=-{\frac {2}{x}}\\x^{3/2}&={\frac {1}{2}}\\x&=\left({\frac {1}{2}}\right)^{2/3}={\frac {1}{\sqrt[{3}]{4}}}\end{aligned}}$ And so since y = -2/x we have $\displaystyle B=\left({\frac {1}{\sqrt[{3}]{4}}},-2{\sqrt[{3}]{4}}\right)$ This allows us to write the desired area as the sum of 2 integrals ${\begin{aligned}{\text{area}}&=\int _{0}^{\frac {1}{\sqrt[{3}]{4}}}\left((-x)-(-4{\sqrt {x}})\right)\,dx+\int _{\frac {1}{\sqrt[{3}]{4}}}^{\sqrt {2}}\left((-x)-(-{\frac {2}{x}})\right)\,dx\\&=\int _{0}^{\frac {1}{\sqrt[{3}]{4}}}\left(-x+4{\sqrt {x}}\right)\,dx+\int _{\frac {1}{\sqrt[{3}]{4}}}^{\sqrt {2}}\left(-x+{\frac {2}{x}}\right)\,dx\\&=\left[-{\frac {x^{2}}{2}}+{\frac {4\cdot 2}{3}}x^{3/2}\right]_{0}^{\frac {1}{\sqrt[{3}]{4}}}+\left[-{\frac {x^{2}}{2}}+2\ln(x)\right]_{\frac {1}{\sqrt[{3}]{4}}}^{\sqrt {2}}\\&=-{\frac {(2^{-2/3})^{2}}{2}}+{\frac {8}{3}}(2^{-2/3})^{3/2}+0-0-{\frac {({\sqrt {2}})^{2}}{2}}+2\ln({\sqrt {2}})+{\frac {(2^{-2/3})^{2}}{2}}-2\ln(2^{-2/3})\\&={\frac {4}{3}}-1+\ln(2)+{\frac {4}{3}}\ln(2)\\&={\frac {1}{3}}+{\frac {7}{3}}\ln(2)\end{aligned}}$

{{#incat:MER CT flag||

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Area between two curves, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag

}}