Science:Math Exam Resources/Courses/MATH104/December 2013/Question 04

MATH104 December 2013

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q1 (l)  •  Q1 (m)  •  Q1 (n)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q2 (e)  •  Q2 (f)  •  Q2 (g)  •  Q3  •  Q4  •  Q5  •  Q6 (a)  •  Q6 (b)  •  Q6 (c)  •  

   Other MATH104 Exams

  •  December 2014  •  December 2011  •  December 2010  •  December 2012  •  December 2013  •  December 2015  •  December 2016  •  

Question 04
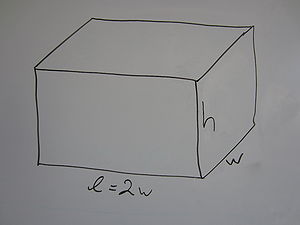
A rectangular storage container with an open top is to have volume of 8 cubic metres. The length of its base is twice the width. Material for the base costs $4.50 per square metre, and material for the sides costs $6 per square metre. Find the cost of the material for the cheapest such container.

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
A simple picture here can get you started. The two constraints let you reduce this to a single variable problem.

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. We wish to minimize the cost, C, subject to the constraint that the length of the base is twice it's width and that the volume of the container must be $V=8{\text{m}}^{3}$. The cost C can be expressed as the sum of the costs for all the sides. Recall that this is an open-top box (i.e., no top). If we let l, w, and h denote the length, width, and height of the box in metres, respectively, then: ${\begin{aligned}C&=C_{\text{sides}}+C_{\text{bottom}}\\&=6(2hw+2hl)+4.5(lw)\end{aligned}}$ since material for the base costs $4.50 per square metre, and material for the sides costs $6 per square metre. We are also given the constraint $\displaystyle V=lwh=8$ Using the fact that the length is twice the width (i.e., l = 2w), the cost function and volume constraint are expressed as $\displaystyle C=36hw+9w^{2},\quad V=2w^{2}h=8$ To reduce this into a single variable problem, we use the constraint to express the height of the box in terms of the width: $h={\frac {4}{w^{2}}},$ and substitute this into the cost function C, making it a function of w only: $C(w)={\frac {144}{w}}+9w^{2}$ To optimize C, we determine first determine its critical points by differentiating with respect to w and setting the derivative equal to zero: ${\begin{aligned}C'(w)&=-{\frac {144}{w^{2}}}+18w\\0&=-{\frac {144}{w^{2}}}+18w\\144&=18w^{3}\\8&=w^{3}\\w&=2\end{aligned}}$ Therefore w = 2 is a critical point. To determine whether or not it is the point that minimizes C, we use the second derivative test. The second derivative of C with respect to w is $C''(w)={\frac {288}{w^{3}}}+18$ which is clearly greater than zero when w = 2. Thus, by the second derivative test, C has a local minimum at w = 2 (Moreover, it is the global minimum since there are no other critical points.) Substituting w = 2 into the cost function, we determine that the minimum cost is $C(2)={\frac {144}{2}}+9(2)^{2}=72+36={\color {blue}\$108}$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER QGT flag, MER Tag Optimization, Pages that use a deprecated format of the math tags, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag