Science:Math Exam Resources/Courses/MATH104/December 2012/Question 05 (b)

MATH104 December 2012

  •  Q1 (a)  •  Q1 (b)  •  Q1 (c)  •  Q1 (d)  •  Q1 (e)  •  Q1 (f)  •  Q1 (g)  •  Q1 (h)  •  Q1 (i)  •  Q1 (j)  •  Q1 (k)  •  Q1 (l)  •  Q1 (m)  •  Q1 (n)  •  Q1 (o)  •  Q2 (a)  •  Q2 (b)  •  Q2 (c)  •  Q2 (d)  •  Q2 (e)  •  Q3  •  Q4 (a)  •  Q4 (b)  •  Q4 (c)  •  Q5 (a)  •  Q5 (b)  •  Q6 (a)  •  Q6 (b)  •  Q6 (c)  •  Q6 (d)  •  

   Other MATH104 Exams

  •  December 2014  •  December 2011  •  December 2010  •  December 2012  •  December 2013  •  December 2015  •  December 2016  •  

Question 05 (b)
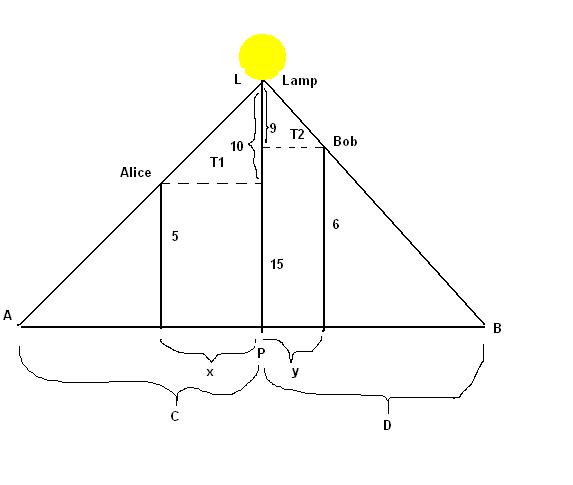
Alice is 5 ft tall and Bob is 6 ft tall. At some instant they are both walking towards a street lamp 15 ft high with Alice west of the lamp and Bob east of the lamp. Suppose at this instant, Alice is walking at 4 ft/s and the distance between the tips of their shadows is decreasing at 11 ft/s. How fast is Bob walking?

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1

This question heavily relies on understanding the problem and the diagram in part (a) and thus all notation here out refers to the diagram in part (a). The diagram labels the important triangles and values. The key relationships needed are in $T_{1}$ (from Alice's head to the lamp post to L), triangle APL, $T_{2}$ (from Bob's head to the lamp post to L), and triangle BPL. Let C denote the length of the segment AP and let D denote the length of the segment BP. The next hints will be successions of understanding what the values are with respect to these letters.

Hint 2

We are given that ${\frac {dx}{dt}}=-4$ (notice that the negative is here since the size of x is decreasing over time as Alice and Bob are walking towards the lamppost). Notice that the distance between the tips of the shadows is given by $C+D$. Thus, we are also given that ${\frac {d(C+D)}{dt}}={\frac {dC}{dt}}+{\frac {dD}{dt}}=-11$ (notice that the negative is here since the distance is decreasing over time as given by the question).

Hint 3
Bob's distance to the lamp is y and so the speed he is walking is ${\frac {dy}{dt}}$. What do we expect the sign of this number to be in the end? Use similar triangles for the triangles mentioned in hint 1 using the picture from part (a) and relate all these hints to create a solution.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution 1

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. The diagram from part a has been recopied for ease of reading Proceeding via the hints, we are interested in solving for ${\frac {dy}{dt}}$. We first note that triangles $T_{2}$ and triangle BPL are similar (they share an angle and both contain a 90 degree angle). Thus, we have that ${\frac {y}{9}}={\frac {D}{15}}$. Multiplying by 15, reducing and differentiating with respect to time gives ${\frac {5}{3}}{\frac {dy}{dt}}={\frac {dD}{dt}}$. To solve for ${\frac {dy}{dt}}$ we will need ${\frac {dD}{dt}}$, the speed at which Bob's shadow tip is changing. To do this we consider that the distance between the two tips is decreasing by 11ft/s and so ${\frac {dC}{dt}}+{\frac {dD}{dt}}=-11$. To determine ${\frac {dC}{dt}}$ we turn to the similar triangle problem for Alice. Triangles $T_{1}$ and triangle APL are similar (they share an angle and both contain a 90 degree angle). Thus, we have that ${\frac {x}{10}}={\frac {C}{15}}$ Multiplying by 15, reducing and differentiating with respect to time gives ${\frac {3}{2}}{\frac {dx}{dt}}={\frac {dC}{dt}}$ We are given that ${\frac {dx}{dt}}=-4$ and so we have that ${\frac {dC}{dt}}=-6$. Therefore we have that ${\frac {dD}{dt}}=-11-{\frac {dC}{dt}}=-5$ and finally then that ${\frac {dy}{dt}}={\frac {3}{5}}{\frac {dD}{dt}}=-{\frac {3}{5}}(5)=-3$ and so Bob is walking towards the lamppost at 3ft/s. Notice the sign we get makes sense because we are told that each person is walking towards the lamp in the question!

Solution 2

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. The diagram from part a has been recopied for ease of reading Proceeding via the hints, we are interested in solving for ${\frac {dy}{dt}}$. We first note that triangles BBob and triangle BPL are similar (they share an angle and both contain a 90 degree angle). Thus, we have that ${\frac {D-y}{6}}={\frac {D}{15}}$. Multiplying by 30, reducing and differentiating with respect to time gives ${\frac {dD}{dt}}={\frac {5}{3}}{\frac {dy}{dt}}$. To solve for ${\frac {dy}{dt}}$ we will need ${\frac {dD}{dt}}$, the speed at which Bob's shadow tip is changing. To do this we consider that the distance between the two tips is decreasing by 11ft/s and so ${\frac {dC}{dt}}+{\frac {dD}{dt}}=-11$. To determine ${\frac {dC}{dt}}$ we turn to the similar triangle problem for Alice. Triangles AAlice and triangle APL are similar (they share an angle and both contain a 90 degree angle). Thus, we have that ${\frac {C-x}{5}}={\frac {C}{15}}$ Multiplying by 15, reducing and differentiating with respect to time gives ${\frac {3}{2}}{\frac {dx}{dt}}={\frac {dC}{dt}}$ We are given that ${\frac {dx}{dt}}=-4$ and so we have that ${\frac {dC}{dt}}=-6$. Therefore we have that ${\frac {dD}{dt}}=-11-{\frac {dC}{dt}}=-5$ and finally then that ${\frac {dy}{dt}}={\frac {3}{5}}{\frac {dD}{dt}}=-{\frac {3}{5}}(5)=-3$ and so Bob is walking towards the lamppost at 3ft/s. Notice the sign we get makes sense because we are told that each person is walking towards the lamp in the question!

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Related rates, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag