Science:Math Exam Resources/Courses/MATH102/December 2016/Question B 06 (b)

MATH102 December 2016

  •  QA 1  •  QA 2  •  QA 3  •  QA 4  •  QA 5  •  QA 6  •  QA 7  •  QA 8  •  QB 1  •  QB 2  •  QB 3(a)  •  QB 3(b)  •  QB 3(c)  •  QB 4(a)  •  QB 4(b)  •  QB 4(c)  •  QB 5(a)  •  QB 5(b)  •  QB 6(a)  •  QB 6(b)  •  QB 7(a)  •  QB 7(b)  •  QB 7(c)  •  QB 8  •  

   Other MATH102 Exams

  •  December 2014  •  December 2011  •  December 2012  •  December 2013  •  December 2016  •  December 2015  •  

Question B 06 (b)

For both parts of this question, consider the function $f(x)=4x^{3}-12x^{2}+9x.$ (b) The absolute maximum of the function $g_{p}(x)=f(x-p)$ on the interval $[0,2]$ is a number that depends on $p$ and can be thought of as a function. Call that function $M(p)$ and calculate it for $p\in [0,2].$ You can use function notation in your answer (e.g. $f(x)$ instead of $4x^{3}-12x^{2}+9x$). Hint: sketch $g_{p}(x)$ for several values of $p$

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hints below. Read the first one and consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it! If after a while you are still stuck, go for the next hint.

Hint 1
The graph of $f(x-p)$ is the one obtained by translating the graph of $f(x)$ by $+p$.

Hint 2
Recall that $f$ is a strictly increasing function.

Checking a solution serves two purposes: helping you if, after having used all the hints, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

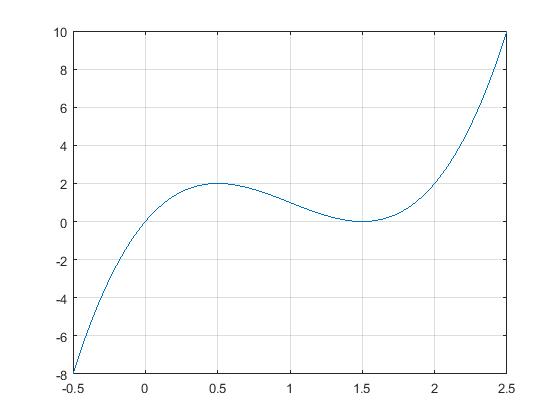
Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. As we mentioned in the Hint 1, the graph of $f(x-p)$ is obtained by translating the graph of $f$ horizontally by $p$. Note that the shape of the graph doesn't change under the translation. From part (a), we know that $f$ is strictly increasing on $\left(-\infty ,{\frac {1}{2}}\right)\cup \left({\frac {3}{2}},\infty \right)$, and strictly decreasing on $\left({\frac {1}{2}},{\frac {3}{2}}\right)$. Also, $f$ has its maximum value $2$ at $x={\frac {1}{2}}$ and $x=2$. Based on this, we can draw the following graph of $f$; From the graph we can easily see that if we move the graph of $f$ horizontally to the left (i.e.,p<0), the maximum occurs at $x=2$, because of $f(x)>f(2)$ for $x>2$. Therefore, for $p<0$, the function $g_{p}(x)=f(x-p)$ has its maximum $g_{p}(2)=f(2-p)$, so that $M(p)=f(2-p)$. On the other hand, for any $x<2$, we have $f(x)\leq f(2)=2$ and actually $f(x)=2$ only occurs at $x={\frac {1}{2}}$ in the range $(-\infty ,2)$. This implies that when we move the graph of $f$ horizontally to the right (i.e.,p>0), if ${\frac {1}{2}}+p$ is in $[0,2]$, the maximum of $g_{p}(x)=f(x-p)$ is $2$. Therefore, for $0<p\leq {\frac {3}{2}}$, we get $M(p)=2$. (by part (a), when $p=0$, we also have $M(p)=2$. Furthermore, if we move the graph of $f$ horizontally to the right by $p>{\frac {3}{2}}$, (i.e, $p+{\frac {1}{2}}>2$), the graph is strictly increasing on $[0,2]$, so that the maximum occurs at $x=2$. As a result, $M(p)=f(2-p)$ for $p>{\frac {3}{2}}$. To sum, we have $\color {blue}M(p)={\begin{cases}2&0\leq p\leq {\frac {3}{2}}\\f(2-p)&otherwise\end{cases}}$