Science:Math Exam Resources/Courses/MATH102/December 2014/Question C 02 (c)

MATH102 December 2014

  •  QA 1  •  QA 2  •  QA 3  •  QA 4  •  QA 5  •  QA 6  •  QA 7  •  QA 8  •  QB 1  •  QB 2  •  QB 3  •  QB 4  •  QB 5  •  QB 6  •  QB 7  •  QC 1  •  QC 2(a)  •  QC 2(b)  •  QC 2(c)  •  QC 2(d)  •  QC 3  •  

   Other MATH102 Exams

  •  December 2014  •  December 2011  •  December 2012  •  December 2013  •  December 2016  •  December 2015  •  

Question C 02 (c)
The graphs to the right show two functions, Graphs $P(c)=P_{m}{\frac {c^{2}}{k^{2}+c^{2}}},\quad D(c)=rc$ where $P_{m}=5$, $k=10$ and $r=1/5$. Suppose that $c(t)$ is the concentration of a substance involved in a chemical reaction and satisfies the equation ${\frac {dc}{dt}}=P(c)-D(c).$ If the concentration is initially $c(0)=8$, what concentration does $c(t)$ eventually approach?

Make sure you understand the problem fully: What is the question asking you to do? Are there specific conditions or constraints that you should take note of? How will you know if your answer is correct from your work only? Can you rephrase the question in your own words in a way that makes sense to you?

If you are stuck, check the hint below. Consider it for a while. Does it give you a new idea on how to approach the problem? If so, try it!

Hint
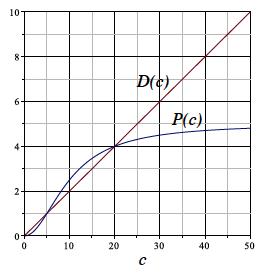
Is the derivative $dc/dt$ positive or negative at $c(0)=8$? Will the function increase or decrease after $t=0$?

Checking a solution serves two purposes: helping you if, after having used the hint, you still are stuck on the problem; or if you have solved the problem and would like to check your work. If you are stuck on a problem: Read the solution slowly and as soon as you feel you could finish the problem on your own, hide it and work on the problem. Come back later to the solution if you are stuck or if you want to check your work. If you want to check your work: Don't only focus on the answer, problems are mostly marked for the work you do, make sure you understand all the steps that were required to complete the problem and see if you made mistakes or forgot some aspects. Your goal is to check that your mental process was correct, not only the result.

Solution

Found a typo? Is this solution unclear? Let us know here. Please rate my easiness! It's quick and helps everyone guide their studies. Observe that $P(c(0))-D(c(0))=P(8)-D(8)>0,$according to the graph. Therefore, ${\frac {dc}{dt}}(0)=P(c(0))-D(c(0))$ is positive initially, so that $c$ would increase with time. On the other hand, the value $c(0)=8$ falls in the interval $(5,20)$, i.e., $5<8<20$. Remember that when the graphs of $P(c)$ and $D(c)$ intersect, we have ${\frac {dc}{dt}}=P(c)-D(c)=0$. In other words, the steady states $c$ are obtained at the intersection points. In the graph, when we start from $c(0)=8$ and move to the right (because it increases with time), the first steady state that we meet is $c=20$. Therefore, $c$ approaches the steady state $c=20$. Answer: $\color {blue}c=20$

Click here for similar questions

MER QGH flag, MER QGQ flag, MER QGS flag, MER RT flag, MER Tag Steady state and equilibrium, Pages using DynamicPageList3 parser function, Pages using DynamicPageList3 parser tag