Course:CPSC522/Multi-Attribute Utility

Multi-Attribute Utility

Multi-attribute utility offers a mathematical model for evaluating and choosing between options when there are multiple reasons to consider when making the choice.

Page Author

Celeste/Clair Ross

Project papers

Doubly Robust Policy Evaluation and Learning

Interactive Multi-Objective Off-Policy Optimization

Abstract

This page briefly goes over utility functions in machine learning and extends that to explain multi-attribute utility functions. It provides examples to help illustrate real-world scenarios of where and why this concept can be applied. It explains how multi-attribute utility functions work and explains the evaluation and optimization process. It introduces off-policy estimators, two of which, the direct method and inverse propensity scoring, are used in Doubly Robust Policy Evaluation and Learning to come up with the doubly-robust approach. These three estimators are then used in Interactive Multi-Objective Off-Policy Optimization to show that the interactive multi-objective off-policy optimization algorithm, or IMO³, provides better performance for off-policy estimators, particularly for estimators that are better than others, like the doubly robust evaluator.

Builds on

This builds on Utility (see Wikipedia until the course page is completed), a mathematical model for making decisions by applying a value to each choice. This page goes explores when a choice is motivated by multiple, often competing, reasons.

Related pages

There are currently no other pages that build on this page. A full list of backlinks (links that reference this page) has been provided in this section.

Backlinks

• Course:CPSC522 ‎ (← links)
• Course:CPSC522/Utility ‎ (← links)
• Course:CPSC522/Multi-Attribute Utility (transclusion) ‎ (← links)

Introduction

Choices are made every day by people, organizations and any number of others agents. Most of these choices are not random (or stochastic), instead, there are informed reasons. To mathematically recreate this mimetic behaviour we can use a utility function. If there are multiple reasons that must be considered when choosing an option we call each reason an attribute and use a multi-attribute utility function.

Utility functions are often used in economic contexts but they also have a growing use for reinforcement learning in the field of machine learning.

Definition and application

To understand how multi-attribute utility functions work, we start by considering how an agent with objectives may go about achieving those objectives. To do so, the agent acts iteratively, starting each iteration by choosing some context based on the likelihood of each context. Then the agent chooses an action to take based on the context and is rewarded with a value for each objective it has. After this, the probability of what contexts are possible can change, so we start a new iteration.

As the agent acts it also learns how to act with a policy. When there are multiple objectives, the policy dictates which ones the agent prioritizes if objectives are conflicting. Someone who designs these policies, aptly called a designer, may change the priorities of an agent by changing the rewards for the agent's actions towards its objectives, resulting in the agent learning a new policy.

More technically, to find a utility function $u_{\theta }$, we start by defining every possible context as the context space $\mathrm {X}$ and all actions it can take as an action space $\mathrm {A}$. The start of the iteration begins by sampling a context probability distribution $P_{\mathrm {X} }$ at the start of each iteration to get $x\in \mathrm {X}$. Next, the agent determines which action to take, $\alpha \in \mathrm {A}$, based on the likelihood of taking each action in $\mathrm {A}$ given the context $x$ by using a stochastic policy, $\pi (\cdot |x)$. Taking action $\alpha$ gives the agent a reward, $r$, towards each of its objectives based on some reward distribution, $P_{r}(\cdot |x,\alpha )$. That is, for $d\geq 1$ objectives the agent receives a reward vector $r\in [0,1]^{d}$.

The policy space for the stochastic policy is a set of vectors of length $K$ where each term in a vector corresponds with an objective and is a positive value where the sum of all $K$ terms in a vector add up to $1$. This is equivalent to saying that, when we have $K+1$ attributes the stochastic policy samples from a $K$-simplex with $K+1$ vertices, with the simplex denoted as $\Delta _{K}$. Written out in set notation the policy space is $\Pi =\{\pi |\pi (\cdot |x)\in \Delta _{K-1},\forall x\in \mathrm {X} \}$.

The expected value of a policy $\pi$ is a guess at the best policy to use by taking the likelihood of each policy being used and using that to weigh the associated reward values. This can be written as $V(\pi )=\mathbb {E} _{x\sim P_{x},a\sim \pi (\cdot |x),r\sim P_{r}(\cdot |x,a)}[r]$, which is a $d$-dimensional vector whose $i$-th entry, $V_{i}(\pi )$, is the expected value of objective $i$ for policy $\pi$.

Multi-armed bandits and simple regret

Usually, there are not an unlimited amount of resources available to make decisions so we must make a choice with limited time to do so. If a multi-objective policy has a limited amount of time or rounds, $T$, then it is a multi-armed bandit problem, also called a $K$-armed bandit problem.

When a choice is made prematurely there is often some level of regret if it was not the right choice in retrospect. It is because of this that the difference between the utility of a given policy and the optimal policy is called regret. When we have a fixed amount of rounds, $T$, to get a policy as close to optimal as we can, $\pi _{\ast }$, we can calculate the difference in the utility value against the utility value of the optimal policy, $\pi$. This is the simple regret, $R_{T}^{sim}$, which can be expressed as the equation $R_{T}^{sim}=u_{\theta _{\ast }}(V(\pi _{\ast }))-u_{\theta _{\ast }}(V(\pi ))$.

Examples

Examples help motivate the topic of multi-attribute utility functions as they have a wide diversity of applications. Some are controversial like its use in hiring new employees. Other applications are emerging with the potential for mass adoption, such as controlling traffic lights and the flow of traffic.

Hiring decisions

Companies may choose to give benefits to their "best employee". To calculate this some companies have opted to use machine learning and multi-objective utility theory to do so. Factors that influence if an employee is considered better than another include attendance, work output, discipline, and reporting.

This could result in machine learning reinforcing gendered biases in the workplaces due to women doing more non-promotable work than men, like office chores. As the public has become increasingly aware of this trend it has gained notoriety. The majority of US citizens are against this process and believe that a machine learning hiring model would miss the individuality among applicants. At the same time, the majority of US citizens believe this practice would ensure everyone is treated equally, which is not what studies have shown.

Traffic patterns

A traffic light network, or a Traffic Signal Control (TSC), may control the lights of many intersections and needs to manage competing objectives to make sure that traffic in all directions does not become congested during different times of the day and year. Reinforcement learning may be used to optimize these control systems through A/B testing, by gathering information on how a proposed solution affects traffic patterns. This process is iterative, if a designer is not satisfied with the results then a new solution must be created and tested.

An example of topology graph of traffic network.

There are three major issues with this.

1. This can take weeks or months to gather enough data to account for seasonal traffic trends.
2. The number of possible policies is large and often hard to predict how trading off priorities will affect traffic.
3. For a large-scale project such as a municipal project the time requirements and unexpected results make it hard to manage an experiment's treatment and control group.

Utility evaluation and optimization

To measure the quality of a policy it helps to assume there is some optimal policy that the designer would like that can be measured against. However, if that policy is unknown then it has to be estimated with an off-policy learning estimator.

To do that, we need some scalarization vector, $\theta$ that, when applied as a linear program to the estimator ${\hat {V}}(\pi )$, results in the maximum value possible. This can be expressed as the following equation.

${\hat {\pi }}=\arg \max _{\pi \in \Pi }u_{\theta }({\hat {V}}(\pi ))=\arg \max _{\pi \in \Pi }\theta ^{\top }{\hat {V}}(\pi )$.

Figure 1: Bias (upper) and root mean squared error (lower) of the three estimators for classification error.

Figure 2: Classification error of direct loss minimization (upper) and filter tree (lower). Note that the representations used by DLM and the trees differ radically, conflating any comparison between the approaches. However, the Offset and Filter Tree approaches share a similar representation, so differences in performance are purely a matter of superior optimization.

While it might not be possible to find the exact policy, the goal is to find a near-optimal policy.

Optimization estimators

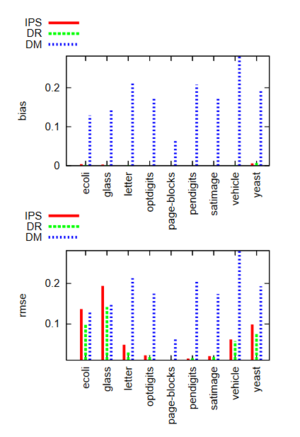
There are three estimators that are the focal point for the research that is being shown here. The direct method (DM), inverse propensity scoring (IPS), and the doubly robust (DR) estimator. The last of these is proposed in Dudìk et al. (2013), the first of the two papers for this assignment.

Direct method

The direct method (DM) estimator uses an offline-learned reward model, ${\hat {r}}(a,x)\in \mathbb {R} ^{d}$, to find the expected reward vector $\mathbb {E} [r|x,a]$, using the equation:

${\hat {V}}^{\text{DM}}(\pi )={\frac {1}{N}}\sum _{j=1}^{N}\sum _{\alpha \in \mathrm {A} }\pi (\alpha |x_{j}){\hat {r}}(\alpha ,x_{j})$

The direct method is prone to bias when the policy isn't known.

Inverse propensity scoring

Inverse propensity scoring (IPS) is less prone to bias than the direct method. IPS uses logged records to correct between the existing logs and the new policies. A propensity score is the probability that a policy takes an action given a context. That is, for a policy $\pi _{0}$, action $a_{j}$, and context $x_{j}$ the propensity is $\pi _{0}(a_{j}|x_{j})$.

IPS can to tuned to be less biased with a hyper-parameter, $M>0$, but at the cost of becoming inconsistent with a high variance in values. The IPS estimator is represented by the following equation.

${\hat {V}}^{\text{IPS}}(\pi )={\frac {1}{N}}\sum _{j=1}^{N}\min \left\{M,{\frac {\pi (\alpha _{j}|x_{j})}{\pi _{0}(\alpha _{j}|x_{j})}}\right\}r_{j}$

Doubly robust

The doubly robust (DR) evaluator is put forward in the first of the two researched papers and builds off the DM and IPS estimators. DR is shown to have a lower variance than IPS if either one of two conditions is met:

1. The propensity scores are correct
2. The reward model is unbiased

Only one of these conditions needs to be met and if the reward model is unbiased, the error can be bounded like in the IPS estimator. The equation for the doubly robust estimator is the following equation.

${\hat {V}}^{\text{DR}}(\pi )={\frac {1}{N}}\sum _{j=1}^{N}{\frac {\pi (\alpha _{j}|x_{j})}{\pi _{0}(\alpha _{j}|x_{j})}}(r_{j}-{\hat {r}}(\alpha _{j},x_{j}))+{\hat {V}}^{\text{DM}}(\pi )$

The IMO³ algorithm

With IMO³ the goal is to gather a group of good policies and then, after a fixed amount of iterations, present them to the policy designer all at once. IMO³ is a general non-adaptive algorithm which means that the estimator used will not change but the scalarization vector, $\theta$, can change over time after incorporating the designer's feedback.

IMO³ identifies near-optimal policies with high probability, but this is dependent on the amount of feedback there is from the policy designer and the training data for off-policy estimation.

How it works

Algorithm 1: IMO³ pseudocode

Input: Logging policy $\pi _{0}$, logged data ${\mathcal {D}}$, budget $T$, and pre-selection budget $L$.

 1: ${\mathcal {W}}\leftarrow \{\}$
 2: for $i={\text{1,...,}}L$ do
 3:     ${\text{Sample }}\theta _{i}{\text{ from a unit ball in }}\mathbb {R} ^{d}$
 4:     $\pi _{i}\leftarrow \arg \max _{\pi \in \Pi }u_{\theta _{i}}({\hat {V}}(\pi ))$
 5:     ${\mathcal {W}}\leftarrow {\mathcal {W}}+\{\pi _{i}\}$
 6: $P_{G}({\mathcal {W}})\leftarrow {\text{ G-optimal design over }}{\mathcal {W}}$
 7: for $t$ = 1,...,$T$ do
 8:     $\pi _{t}\sim P_{G}(W)$
 9:     ${\text{Present }}{\hat {V}}(\pi _{t}){\text{ to the designer and observe }}Y_{i}$
 10: ${\hat {\theta }}\leftarrow$ ${\text{MLE}}(\{{\hat {V}}(\pi _{t}),Y_{t}\}_{t=1}^{T})$
 11: ${\text{Return }}{\tilde {\pi }}_{\text{*}}\leftarrow \arg \max _{\pi \in \Pi }u_{\hat {\theta }}({\hat {V}}(\pi ))$

Figure 1: Simple regret of different algorithms for a fixed logged data size $N=20,000$ and varying interaction budget. Each experiment is averaged over 10 logged data, 10 randomly selected $\theta _{\ast }$ and 5 runs under each combination of logged data and $\theta _{\ast }$.

Figure 2: Simple regret of different algorithms for a fixed interaction budget $T=100$ and varying logged data size. Each experiment is averaged over 10 logged data, 10 randomly selected $\theta _{\ast }$ and 5 runs under each combination of logged data and $\theta _{\ast }$.

Figure 3: Simple regret of different algorithms by fixing logged data size $N=20,000$ and varying budget. Each experiment is averaged over 10 logged data, 10 randomly selected $\theta _{\ast }$ and 5 runs under each combination of logged data and $\theta _{\ast }$.

Figure 4: Simple regret of different algorithms by fixing budget $T=100$ and varying logged data size. Each experiment is averaged over 10 logged data, 10 randomly selected $\theta _{\ast }$ and 5 runs under each combination of logged data and $\theta _{\ast }$.

Briefly, the algorithm consists of considering a fixed time spent gathering policies, finding the best candidates to present to the designer, and using the best policy of the group after incorporating the designer's feedback before starting again.

More formally, the first challenge is that the possible policies are a continuous and infinite set, $\Pi$. To overcome this, that policy space is discretized to a new set ${\mathcal {W}}$ that is split into $L$ diverse policies.

To do this discretization of the policies involves learning what the scalarized vector should be, or rather, learning what the maximum likelihood estimate (MLE) is, which poses an efficiency challenge. To address this G-optimality is used. This method tries to minimize the maximum entry in a diagonal of the hat matrix $X(X^{\top }X)^{-1}X^{\top }$ which minimizes the maximum variance of the predicted values.

With our discretized policy space and $L$ policies we spend a specified number of rounds, $T$, querying the designer. For an objective value $v$, the designer uses a logistical response model to respond with a probability $\ell _{\theta _{\ast }}(v)$ that a policy is acceptable.

$\ell _{\theta _{\ast }}(v)=1/1+\exp(-u_{\theta _{\ast }}(v)))$

In round $t\in [T]$, we draw a policy $\pi _{t}$ and present its values ${\hat {V}}(\pi t)$ to the designer. The response from the designer is $Y_{t}\sim {\text{Bern}}(\ell _{\theta _{\ast }}({\hat {V}}(\pi _{t})))$ where ${\text{Bern}}(\mu )$ is the Bernoulli distribution with mean $\mu$.

Finally, we find the MLE ${\hat {\theta }}$ from the collected observations and use it to identify the optimal policy ${\tilde {\pi }}_{\ast }$ among them.

Using estimators with IMO³

The way the second paper builds on the first is that IMO³ uses the doubly robust estimator as a baseline for performance. Since the DR estimator is slightly better than DM and ISP, the experiment results from Figure 3 and Figure 4 show that using a better off-policy estimator with IMO³ provides better performance.

Future work

IMO³ adopted a simple non-adaptive algorithm here but in the future, there is room to generalize (and analyze) more complex utility functions, and other types of feedback and response models.