Course:CPSC522/Genetic Algorithms
Title
Genetic algorithms optimize functions by imitating evolutionary biology.
Principal Author: Jeffrey Niu
Collaborators:
Abstract
Genetic algorithms are a form of evolutionary computation. These algorithms draw inspiration from biology to find solutions to complex problems. In this page, we discuss the basics of genetic algorithms and provide a simple example of applying a genetic algorithm to maximize a function. Then, we discuss the applications of genetic algorithms, including evolutionary reinforcement learning.
Builds on
Neural Networks were born out of the same overarching premise of evolutionary computing as neural networks used neuroscience for inspiration. The field of evolutionary computing builds on Artificial General Intelligence, as some pioneers of artificial intelligence were looking to build artificial life. Evolutionary reinforcement learning builds upon Reinforcement Learning.
Related Pages
Genetic algorithms are similar to Control Theory and Multi-Agent Systems, as genetic algorithms can also be applied to decision making for intelligent agents.
Content
Background
In the early ages of artificial intelligence, scientists wanted to build programs that could learn and interact with their environment. They looked toward biological systems for inspiration for a model for an intelligent agent. These ideas blossomed into two fields, machine learning, led by neural networks, and evolutionary computing, which includes genetic algorithms.
The first version of genetic algorithms was invented by John Holland in the 1960s. Holland envisioned a simulation of Darwinism, which centered around the survival of the fittest. He also wanted to include the biological processes that contributed to genetic diversity such as crossing over, genetic mutations, recombination, and inversion.
As computational problems became more complex, exhaustive search algorithms were rendered infeasible. Other problems arose that required the algorithm to adapt to their environment, such as a robot's actions in a changing environment. Genetic algorithms are a candidate heuristic for these problems as the algorithm could evolve according to the environment while exploring the search space through genetic variations.
Genetic Algorithms
There are five main components when building a genetic algorithm:
- A fitness function that the algorithm aims to optimize. A simple fitness function can be a univariate function such as .
- A set of possible chromosomes. These chromosomes define the search space where we wish to find the optimal chromosome with respect to the fitness function. For the univariate function above, our search space may be integers between 0 and 15, where the optimal solution for maximizing the function is 10. To encode the chromosomes, we may simply use a 4-bit representation ranging from 0000 to 1111.
- A selection method to determine which chromosomes will reproduce and get passed down to the next generation. Generally, we will sample the chromosomes randomly, where chromosomes that are closer to optimality are given higher probability. In this example, since is non-negative over the search space, we can define the probability for each chromosome as . This method is called the roulette wheel method. In cases where the function is not non-negative, other formulations can be used.
- A crossover method to produce chromosomes of the next generation. Crossovers refer to swapping parts of the two parental chromosomes to produce two new child chromosomes. This is analogous to the children inheriting both maternal and paternal traits. However, in a genetic algorithm, we always have two children at once. In our example, one crossover method is to randomly choose an index from 0 to 4 and swap the bits before the index. We can also attach a probability that crossing over will occur, . For example, if the two parental chromosomes were and , and we sampled index 2, the children chromosomes would be and . Note that if the index was 0 or 4, no crossover would take place and the children chromosomes would be identical to the parents.
- A mechanism for introducing random mutations into child chromosomes. These random mutations are generated with low probability, such as . A mutation causes a random part of the chromosome to change to another value. In our example, a mutation would be a random bit flip at any index.
With these five components, the procedure for a genetic algorithm is straightforward. We start with a sample of random starting chromosomes. From there, we iteratively evaluate the chromosomes on the fitness function, select which ones will reproduce, perform crossover and mutations, terminating upon convergence or a certain number of iterations have been reached.
The pseudocode is:
Generate n random chromosomes
Evaluate fitness function f(x) on each chromosome x
Until convergence or max iterations reached do
Evaluate the probability of each chromosome being selected for reproduction P(x)
While there are fewer than n child chromosomes do
Select two chromosomes from the current pool with probabilities given by P(x)
With probability p_c, perform crossover
Mutate the child chromosomes with probability p_m
end
Replace the parent pool with the children
end
There are more advanced formulations for each of the five components, which are mentioned in a review article by Katoch, Chauhan, & Kumar.
Example
Now, we can attempt to maximize a function with two variables over the range , .
Naturally, our fitness function is just . The set of possible chromosomes will be the concatenated binary representation of and . For example, is the chromosome .
However, this function can be negative, so the probability function from above will not work. Instead, we can use a selection followed by ranking scheme. Of the parent chromosomes, we remove half of them from consideration (assume is divisible by two for simplicity). The remaining chromosomes are sorted and assigned a rank . Then, their selection probability is given byFor example, if there were chromosomes, there would be six remaining after halving. Then, a chromosome with rank 1 would have probability as . Likewise, , , and so on.
We will use the same crossover and mutation method.
Initial chromosomes
First, we generate a random set of 12 starter chromosomes. In our initial set of chromosomes, the average fitness was 725.83 while the maximum was 2600. Here, the selection probability is calculated using the formula above.
| Number | Chromosome | () | Selection Probability | |
|---|---|---|---|---|
| 1 | 11000100 | (12, 4) | 584 | 1/21 |
| 2 | 00100100 | (2, 4) | -496 | 0 |
| 3 | 01100111 | (6, 7) | 188 | 0 |
| 4 | 11011011 | (13, 11) | 1886 | 4/21 |
| 5 | 00000111 | (0, 7) | -1000 | 0 |
| 6 | 10100110 | (10, 6) | 600 | 2/21 |
| 7 | 01000100 | (8, 8) | 504 | 0 |
| 8 | 01000011 | (8, 3) | 184 | 0 |
| 9 | 01100000 | (6, 0) | -64 | 0 |
| 10 | 11111011 | (15, 11) | 2600 | 6/21 |
| 11 | 11001110 | (12, 14) | 2024 | 5/21 |
| 12 | 11110111 | (15, 7) | 1700 | 3/21 |
Produce the Second Generation
Using the selection probabilities above, we will sample six pairs of chromosomes to generate 12 new chromosomes. Each row in the table shows a pair of chromosomes. A vertical bar shows the position for crossing over. Since mutations are very rare, we are unlikely to see one in one generation. However, for the sake of demonstration, we can introduce a mutation, indicated in bold.
| Numbers | Mating Pair | New Chromosomes | ||
|---|---|---|---|---|
| 6
10 |
1010011|0
1111101|1 |
10100111
11111010 |
(10, 7)
(15, 10) |
700
2375 |
| 10
11 |
1111|1011
1100|1110 |
11111110
11001011 |
(15, 14)
(12, 11) |
3275
1592 |
| 11
4 |
11|001110
11|011011 |
11011011
11001110 |
(13, 11)
(12, 14) |
1886
2024 |
| 10
12 |
11111|011
11110|111 |
11111111
11110011 |
(15, 15)
(15, 3) |
3500
800 |
| 1
10 |
|11000100
|11111011 |
11000000
11111011 |
(12, 0)
(15, 11) |
8
2600 |
| 11
12 |
110011|10
111101|11 |
11001111
11110110 |
(12, 15)
(15, 6) |
2168
1475 |
In the second generation, the average fitness is now 1866.9 and the maximum is 3500, which happens to be the global maximum in our search space. We will continue for more generations until the chromosomes are all the same, or we reach a certain number of iterations.
The table below shows another execution on the same function over multiple generations. While the maximum fitness reaches the global maximum in three generations, the algorithm converges at generation 8 as all chromosomes are the same.
| Gen 1 | Gen 2 | Gen 3 | Gen 4 | Gen 5 | Gen 6 | Gen 7 | Gen 8 | |
|---|---|---|---|---|---|---|---|---|
| Avg Fitness | 441.3 | 1301.6 | 2430.8 | 3099.2 | 3270.8 | 3343.7 | 3458.7 | 3500 |
| Max Fitness | 3050 | 3275 | 3500 | 3500 | 3500 | 3500 | 3500 | 3500 |
Applications of Genetic Algorithms
Next, we will review some of the modifications and applications to genetic algorithms to model different types of problems.
Flexible Job-shop Scheduling
A classical problem in algorithms is the problem of job-shop scheduling. In the flexible job-shop scheduling (FJSP) variant, we have a series of jobs , each of which has a different number of operations . These operations must be scheduled on machines , where each machine can only run one operation at a time and the operation cannot be interrupted midway. There is an associated running time for running operation on machine , . The goal is to find an assignment of operations to machines that minimizes the total length of the schedule.
There are many possible assignments in this combinatorial problem, which makes it difficult to find an optimal solution. In fact, it is NP-hard as it is a case of the travelling salesman problem. Thus, genetic algorithms can help find an optimal solution quickly. Different genetic algorithms have been proposed for FJSP including those by Teeking & Thammano (2012), Driss, Mouss, & Laggoun (2014), and Zhang, Gao, & Shi (2011). Here, we provide an overview the first algorithm. To demonstrate the genetic algorithm setup, consider the following FJSP with three machines and two jobs with three operations each:
| Job | Operation | Machine | ||
|---|---|---|---|---|
| 2 | 4 | 8 | ||
| 5 | 4 | 7 | ||
| 2 | ||||
| 5 | 6 | 5 | ||
| 6 | 5 | |||
| 2 | 6 | |||

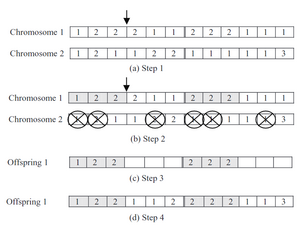
- Chromosomes: The chromosome consists of two halves. Each half has length equal to the total number of operations, which in this case is six. The first half describes which job and operation is located at the corresponding index in the second half. The number is the job number , and the -th occurrence of that number represents -th operation. The second half describes the assignment of the operation to a machine. Consider the following chromosome: . The first index from the first half indicates the first job's first operation, . The corresponding index in the second half indicates that is assigned to . Likewise, the second index means that is assigned to , and the third index indicates is assigned to .
- Fitness function: The fitness of a chromosome is the total length of time computed from the assignment of operations to machines. Figure 1 shows a schedule of the jobs, which concludes that the total length is 16.
- Selection: The algorithm uses a variant of roulette wheel selection. Instead of the two chromosomes being selected independently of each other, the two chromosomes are selected such that pairs of chromosomes that are more similar have a greater chance of being selected together.
- Crossover: The crossover method selects an index in the first half of the chromosome. Then, the operations encoded by the first parental chromosome before the index are incorporated into the child chromosome. Then, the operations that were omitted are taken from the second parental chromosome. In the example in Figure 2, the index selected was 3, and the operations are kept from the first parental chromosome. Thus, are taken from the second parental chromosome.
- Mutation: To mutate, two operations will have their machines swapped, assuming that each operation can be assigned to the other's machine.
Evolutionary Reinforcement Learning
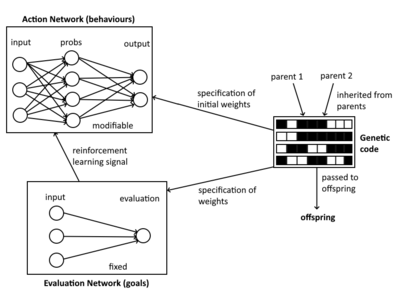
The evolutionary reinforcement learning (ERL) model combines genetic algorithms with reinforcement learning to model ecological systems. This model was motivated by the Baldwin effect, which was an alternative process for evolution which hypothesized that learned behaviours are passed down. In the ERL model, agents interact with an environment containing food, predators, and other objects. Each agent has a state, which includes its internal energy and other characteristics. Agents can reproduce asexually, where random mutations can occur in the offspring, or reproduce sexually, where two agents produce offspring with crossover.
There are three components to the ERL model (Figure 3):
- The genome contains the weights for the neural networks that form the action and evaluation networks.
- The evaluation network takes the agent's current state and provides an evaluation of how good the state is. The evaluation network's weights are fixed for the lifespan of the agent.
- The action network takes the agent's current state and makes an action. These actions can have consequences such as consuming an unit of food, or being eaten by a predator. The initial weights of the action network are specified by the genome, but are modified during the agent's life through a reinforcement learning algorithm.
Given an environment, we can observe which genes become dominant. We can also observe what the agents learn, such as moving towards food and away from predators. The agent's chromosome can also express more complex concepts. For example, in the Echo ecosystem, agents can trade or fight other agents to gain resources.
Interestingly, in this model, the concepts of fitness and selection of chromosomes are no longer explicitly defined. Instead, fitness becomes the ability to reproduce, which mirrors the goals of real-world organisms. The selection of chromosomes, or reproduction, becomes the ability to find a willing mate. To mimic nature, there are genes that encode the willingness of an agent to mate with another based on the traits of the suitor agent.
COBWEB is a software program that uses a similar evolutionary approach to model multiple agent behaviours in a 2D or 3D environment. It includes concepts such as prisoner's dilemma and agent diseases, alongside different types of food and environmental factors. Users have used COBWEB to model changes ecological systems such as the effect of a toxin in Lake Ontario, or to the social sciences such as a model of the Concentric Zone in geography.
The textbook An Introduction to Genetic Algorithms by Melanie Mitchell has further information regarding ERL and its applications.
Other Applications
Genetic algorithms have been applied to many different fields, mostly to find an optimal solution to a problem that are combinatorial. A common application is in operations research, where problems such as scheduling, network design, and forecasting have been tackled using genetic algorithms. A review article by C.K.H. Lee provides an overview of genetic algorithms in operations research. There are also applications of genetic algorithms in medicine, which have been used to detect disease and predict outcomes. A review article by Ghaheri et al. discusses the different applications in medicine.
Current State of Genetic Algorithms
While genetic algorithms were popular in the 1990s, it has largely fallen out of favour compared to deep learning methods such as neural networks. Its impact today is mostly in niche fields where problems can be easily modeled with a genetic algorithm, namely optimization problems like job-shop scheduling.
Weaknesses with genetic algorithms have made it less desirable. These weaknesses include:
- Genetic algorithms may converge on local optima. To counter this, higher mutation rates can be used. However, this can lead to instability as mutations prevent the algorithm from converging on the global optima. In general, the tradeoff between intensification and diversification is difficult to balance.
- The fitness function adds computational complexity. Since we must evaluate the fitness function on all chromosomes at every iteration, complex problems requiring complex fitness functions will increase the computation required.
- Difficulty in modeling a problem. Encoding the problem's search space in a chromosome can be difficult, especially in continuous spaces. The fitness function may also not be appropriate, especially for problems which are binary, such as decision problems. This makes genetic algorithms especially unfavourable compared to current machine learning methods.
Nonetheless, advancements in genetic algorithms have been made, including:
- Multi-objective genetic algorithms: Instead of a single fitness function, there are multiple fitness functions to optimize over. The goal of multi-objective genetic algorithms is to reach the Pareto front, which is the set of solutions where one of the objectives cannot be improved without worsening another objective. This tutorial gives an overview of the different strategies used for multi-objective genetic algorithms.
- Parallel genetic algorithms: We can exploit parallel computing to improve the runtime of genetic algorithms. Some strategies include parallelizing the calculation of the fitness function and selection, or having separate processors compute local solutions and selecting the best solutions from each processor for the next iteration. However, further work is needed to optimize the use of computing resources.
- Chaotic genetic algorithms: The crossover and mutation operations are replaced with chaotic maps. This draws upon chaos theory, which is a branch of mathematics that tries to model disordered and irregular systems. This chaos helps the genetic algorithm explore without converging on a solution too quickly.
- Hybrid genetic algorithms: These mix other local search algorithms with genetic algorithms to reduce the search space to better guide the genetic algorithm to optimal solutions.
A full list of state-of-the-art genetic algorithms, including the variants mentioned above, can be found in section 4 of the review by Katoch, Chauhan, & Kumar.
Annotated Bibliography
Carr, J. (2014). An Introduction to Genetic Algorithms. This paper is a quick and digestible overview of genetic algorithms.
Driss, I., Mouss, K. N., & Laggoun, A. (2015). A new genetic algorithm for flexible job-shop scheduling problems. Journal of Mechanical Science and Technology, 29, 1273-1281.
Emmerich, M. T., & Deutz, A. H. (2018). A tutorial on multiobjective optimization: fundamentals and evolutionary methods. Natural computing, 17, 585-609. This is a tutorial on multi-objective genetic algorithms.
Ghaheri, A., Shoar, S., Naderan, M., & Hoseini, S. S. (2015). The applications of genetic algorithms in medicine. Oman medical journal, 30(6), 406. This review article provides an overview of applications of genetic algorithms in medicine.
Hraber, P. T., Jones, T., & Forrest, S. (1997). The ecology of Echo. Artificial life, 3(3), 165-190. This paper contains Echo, a demonstration of evolutionary reinforcement learning to model ecological systems.
Katoch, S., Chauhan, S. S., & Kumar, V. (2021). A review on genetic algorithm: past, present, and future. Multimedia Tools and Applications, 80, 8091-8126. This review article provides an overview of all the different formulations of a genetic algorithm, including modern approaches. It also mentions limitations of genetic algorithms.
Lee, C. K. H. (2018). A review of applications of genetic algorithms in operations management. Engineering Applications of Artificial Intelligence, 76, 1-12. This review article provides an overview of the applications of genetic algorithms in operations research.
Milošević, M., Lukić, D., Đurđev, M., Vukman, J., & Antić, A. (2016). Genetic algorithms in integrated process planning and scheduling–a state of the art review. Proceedings in Manufacturing Systems, 11(2), 83-88. This is a review of genetic algorithms in process planning and scheduling, which includes flexible job-shop scheduling.
Mitchell, M. (1998). An introduction to genetic algorithms. MIT press. This book provides an in-depth overview of genetic algorithms, including evolutionary reinforcement learning.
Suh, N., Bass, B., Chan, E., & Toller, N. (2003). Emergent Computation and Modelling: Complex organization and Bifurcation within Environmental Bounds(COBWEB). Journal of Environmental Informatics, 1(2), 1-11. This is the initial article describing COBWEB.
Teekeng, W., & Thammano, A. (2012). Modified genetic algorithm for flexible job-shop scheduling problems. Procedia Computer Science, 12, 122-128.
To Add
Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.
|
|