Course:CPSC522/Bounded Rationality

Bounded Rationality

Bounded rationality is a concept that the rationality of a realistic agent is limited by resources such as time, access to information, capacity for information, and processing power, and as such cannot be absolute as rationality is often defined.

Principal Author: Julin Song
Collaborators: Ainaz Hajimoradlou, Bronson Bouchard, Gudbrand Tandberg

Abstract

Bounded rationality is a concept that a realistic agent can only be rational to a certain extent. Deciding on how far that extent should go and then how to reach that point makes interesting problems. This page gives an introduction to bounded rationality as distinguished from unbounded rationality with a little bit of history, a brief discussion of the motivation of the concept in cognitive psychology, then presents overviews of some of bounded rationality's manifestations in computing.

Builds on

Agents modeled with unbounded rationality act to maximize utility, while agents modeled with bounded rationality can only aim for some satisfactory amount of utility. This topic also builds on deviation from strict logic.

Related Pages

Bounded rationality has application in reinforcement learning and multi-agent systems.

Game theory typically assumes unbounded rationality.

Another related concept is rational ignorance.

Content

Herbert Simon (1985). The definition of BR in economics has since deviated from the lack of processing capacity to mean the lack of information, but in regards to computing it is reasonable to assume that the definition remains the same.

Compare to unbounded rationality

Before bounded rationality there was unbounded rationality. It was referred to simply as "rationality" since it was the only kind; it was an absolute and opposed to it was irrationality. The preferences of a rational agent is expected to adhere to the axiom of transitivity. The neoclassical economics due to von Neumann and Morgenstern makes the assumption that groups of agents such as the whole market have approximately unbounded rationality, and as such a generic agent is able to calculate the sum of his expected future utility per action. And because they're able, those agents are always trying to maximize utility. This relatively simple model of the world is still taught today and often used on real problems.

In the 1960s, bounded rationality appeared as a reaction to those sometimes-oversimplified models. It may be too hard to process expected utility to the end of time; there may be more variables than the agent could store even in a limited timeframe; the search space of possible actions may be too large.

"No one wants to do all that!" The boundedly rational agent complains.

Bounded rationality

Herbert Simon first used the words "bounded rationality" in Models of Man: Social and Rational (1957). He suggests that a solution to the problem of limited rationality in agents, that is, a solution to the impossibility of actually maximizing utility, is to simply go for a satisfactory result - he calls this satisficing, a portmanteau of "satisfy" and "suffice". With this assumption, sometimes a boundedly rational model is more tractable than an unboundedly rational model.

Motivation in psychology

Figure 1. Gray rectangles of the same luminance appear to have different brightness when the surrounding color blocks are different.

Humans are often thought of as rational agents. One does not often mention the limitations to that statement and the boundaries beyond which it wouldn't be true. But if humans were always and wholely rational, self-sabotage would not exist. The mind plays games - some sensory, like in Figure 1; others are on a higher level, like loss aversion, context dependence of perception, and framing effect. A human can only assimilate a fraction of the potential stimuli in the environment at each point in time; for perception, this allows retina displays and oil painting. Humans are physically wired to notice change more than static stimuli and to extract the signal amid noise.

The preceding paragraphs discussed the inevitable boundedness of human rationality. Often, decisions that can be made logically do not go through a logical thinking process; for example, muscle memory or taking lethal impact for a loved one. This kind of bounded rationality may be caused by a competition between the unconscious and conscious systems in the brain. The existence of two systems in the brain is known as Dual Process Theory and has been supported by psychological experiments, fMRIs and spectroscopy.

Theories in inattention and selective attention suggest that bounding the number of variables and thus the problem size in a decision when not necessary has evolutionary benefits. Since information acquisition is costly, variables in the "gap" - not important enough but still relevant - are often modeled as unknown but fixed values.

Computing

Sparsity

Figure 2. Limiting bounded rationality so that a model is realistic with weights on all important dimensions but remains tractable would land somewhere in the middle of the spectrum.

The bounded rationality assumption correlates with dense models. Imagine an agent that knows there are $n$ dimensions that have real effects on a problem, where $n$ is very large. With intentions of sparsity, the agent operates on a model that gives most dimensions a weight of 0, making the model realistic yet keeping it tractable. In finding an appropriate model, the agent also needs to avoid Herbert Simon's problem of infinite regress, i.e., spending more resources on finding the optimal simplification of the problem than solving the original problem. Figure 3 shows one algorithm for finding a sparse model, which (1) looks for a computing model $m$ that minimizes the difference between the value of the it and that of the true model $\mu$ with a certain action $a$, all with a penalty for additional non-zero dimensions while (2) looks for the action that maximizes the value function with a certain model $m$.

Figure 3. Sparse Bounded Rationality Algorithm.

In reality, for both human and computional agents, the retrieval of information is very costly, not least because there is limited space within the agent and within the environment for information storage. Consequently the sparse model's variables are often those that are local or recent information. For pyramidal problems (that is, problems that branch into smaller problems, though not necessarily recursive), there is a tendency to resolve uncertainties early lest the problem size explode.

Emotion

Attention needs to be conserved. Are there ways attention is biologically constrained, other than vicinity of memory? Emotion is a likely candidate. Case in point is fear. Evolutionarily there are obvious benefits where this emotion in particular focuses attention. Although the intricacies of how emotion affects the decision making human agents is not clear, many studies in psychology and economics incorporate their versions of emotion. The main flavors of emotion modeling are categorical, with various lists, and real-valued, with some remix of valence, arousal and dominance. There are different attempts to model emotion in computational agents, but the emotional-Belief-Desire-Intent agents may be the closest to using emotion as a constraint of actions as discussed.

Reinforcement Learning

Figure 4. Approximation of a hidden utility function.

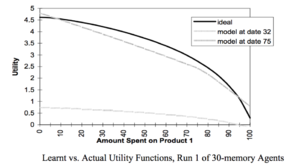
Computational models of bounded rationality are often some flavour of reinforcement learning, and the two are both more or less descended from the concept of animals learning in trial and error. Assumptions of bounded rationality in computation is often that there is a hidden utility function that agents are not explicitly aware of, but it exists. Edmonds (1999) is an early work using evolutionary programming to show that reinforcement learning can closely approximate a hidden utility function within assumptions of bounded rationality.

Further Reading

Prospect theory is related to loss aversion.

Control Theory may be relevant for understanding costly acquisition of information.

To Add

Discuss how Markov Networks and Bayesian Networks are related to BR.

Spiegler R. Bayesian networks and boundedly rational expectations. The Quarterly Journal of Economics. 2016 Mar 7;131(3):1243-90.