Course:CPSC522/Automatic Classification of Morphological Heart Arrhythmia

Automatic Classification of Morphological Heart Arrhythmias

Principal Author: Mehrdad Ghomi

Abstract

ECG of various forms of heart arrhythmia

Here on this page, I will present my hypothesis and the achieved results regarding classification of morphological heart arrhythmias using machine learning techniques. The three techniques that I will discuss and compare their achieved results are K-Nearest Neighbours (k-NN), Neural Networks and Multinomial Logistic Regression. The goal is to detect five types of arrhythmias based on the features extracted from electrocardiography (ECG) signal signal of the patients, without the necessity of an expert in the process. I will utilize the MIT/BIH arrhythmia database which contains thousands of recorded ECG beats of several patients and is publicly available on the PhysioNet website . Different intervals of ECG signals do not have the same level of importance, specifically, the QRS complex is the major interval that needs more focus and contains more valuable information for detection of the arrhythmia type. In order to benefit from the uneven value of different intervals, I utilized Hermite basis functions (Gaussian functions and polynomials) to remodel the signals and use the coefficients of the linear combination of these basis functions as the model parameters (feature vector of size 25). I achieved an accuracy of 99.45% using 1-NN(k-NN with k=1) classifier after remodelling of the feature vector (from 63.54% accuracy), 98.98% using neural networks and 97.31% using Multinomial logistic Regression with L2-regularization. My best result in terms of accuracy (1-NN after remodelling) is 99.45% accurate which is significantly more accurate than the signal-based model and is comparable with expert human-level of accuracy. However, due to computational complexity I will pick my Neural Network method as the most practical classification method.

Motivation

The process of detecting heart arrhythmias from the ECG signals is a labor-intensive task that needs an expert (cardiologist). Also, manual detection can always include human errors which can result in incorrect decisions that can have fatal consequences. Computer programs on the other hand can benefit from machine learning techniques and pattern recognition and after training on the data, can perhaps achieve low error results and classify the various forms of arrhythmias with high precision. Moreover, in a possible futuristic world where many of the jobs are taken by artificial intelligence agents and most of the clinical tasks are done by computer programs/robots rather than medical doctors, this framework can be useful and extendable to other areas of specific illness detection from ECG signals.

Hypothesis

My hypothesis is that there is no need for expert supervision to detect different forms of morphological heart arrhythmias from the ECG signals, and the process can be automated via machine learning techniques such as k-Nearest Neighbors (k-NN), Neural Networks and Multinomial Logistic Regression. I utilized the standard ECG signal data set (hours of heart beats of several patients which resulted in thousands of ECG signal units and their QRS complexes) of MIT/BIH which is available on the PhysioNet.org website to test my results.

Introduction

ECG of a heart in normal sinus rhythm.

The key criterion in diagnosis of morphological heart arrhythmias is ECG signal which reflects the electrical activities of the heart. The shape of the ECG beat and especially the QRS complex, contains valuable information regarding the type of the heart arrhythmia and its diagnosis. There are features from these signals that can be extracted and utilized for the automated process of diagnosis. Heart arrhythmias could be divided into two main categories: non-morphological and morphological. When the position of the main peaks and the amplitude of the signal (especially at QRS complex) are the main features, it is considered non-morphological arrhythmia. On the other hand, when the shape and pattern of the signal vary according to the type of heart disorder, we have morphological arrhythmia. The concavity and convexity of the signals and their structure in the morphological arrhythmia requires attention in the process of detection and treatment. The focus of my project is morphological arrhythmias.
The process of detecting heart arrhythmias from the ECG signals is a labor-intensive task that needs an expert (cardiologist). Also, manual detection can always include human errors which can result in incorrect decisions that can have fatal consequences. Computer programs on the other hand can benefit from machine learning techniques and pattern recognition and after training on the data, can achieve low error results and classify the various forms of arrhythmias with high precision.
Most of the methods used to detect the structure and pattern changes in the ECG signals are based on signal modelling approaches such as Markov models, Autoregressive and Dynamic models. Although these models have been successful and achieved high level of precision, they are very sensitive to small errors and random variations in the shape of the signals corresponding to a specific type of ECG beats. This will result in incorrect decision making and wrong classification. One way to overcome this is to benefit from methods that are more stable and more robust and can detect these minor variations accurately. There are 5 types of ECG beat signals considered in my project which correspond to 5 different arrhythmias and are: N, PVC, APC, RBBB and LBBB.
My contribution is to remove the necessity of expert supervision to detect different forms of morphological heart arrhythmias from the ECG signals. I introduced an automated machine learning framework that can detect and classify these types of morphological heart arrhythmia via 3 different classification approaches: k-Nearest Neighbours (1-NN), neural networks and multinomial logistic regression. I will utilize the standard ECG signal data set of MIT/BIH (hours of heart beats of several patients which resulted in thousands of ECG signal units and their QRS complexes) which is publicly available on the PhysioNet.org website to test my results.
If you are interested to know more about heart arrhythmias further than the necessary level of knowledge to understand this page, click here.

Data

The electrocardiogram (ECG) signals are taken from the MIT/HIB data set. This data set is publicly available at PhysioNet.org and contains hours of ECG beats of many patients which are annotated by specialists (cardiologists). I used a total of 9366 beats for my project and split it into train, validation and test sets. I used a total of 5618 (∼ 60%) beats for training and 1874 (∼ 20%) for validation and 1874 (∼ 20%) for testing. These signals are from 5 different arrhythmias including Atrial Premature Contraction (APC), Premature Ventricular Contraction (PVC), Right Bundle Branch Block (RBBB), Left Bundle Branch Block (LBBB) and normal beat (N). Number of train, validation and test beats for each arrythmia are shown in a table in evaluation section.
Each beat contains 203 samples with the sample rate of 360Hz which were used as feature vector. In terms of optimization and reducing the computation time, it is decided to reduce the size of feature vector into 25 elements. Hermitian Basis Functions (HBF) which are actually a combination of Gaussian functions with polynomials were used to model the entire ECG beat by reproducing the signal via a linear combination of Hermitian basis functions.
If you are interested to have access to the ECG database and perhaps use it for your own projects please click here.

Related Works

To detect morphological arrhythmias it is needed to use methods which enable us to extract the shape and morphological properties of the ECG signal. Lagerholm et al. and Ge et al. proposed some methods to detect the morphology of signal which are generally based on the signal modelling. Although model based methods are successful in detecting morphological arrhythmias, but because of random variations in the shape of the signals corresponding to a specific type of ECG beats, the parameters of the model are not found enough sensitive to trace these changes. This leads to make wrong decisions in the classification levels. To solve the above problem, it is needed to use methods which are able to suppress these variations and to reach more accurate results in arrhythmia detection. Methods based on calculating the higher-order statistics have been powerful for this purpose which were proposed by Osowski et al. .

Background Knowledge

Hermite Basis Functions and Polynomials

As mentioned above, the motivation behind picking Hermite basis functions to model the ECG beat signal is the fact that I can easily model the peak (QRS complex) with a Gaussian function and the fluctuations on the graph with polynomial functions. Hermite polynomials were defined by Laplace (1810) though in scarcely recognizable form, and studied in detail by Chebyshev (1859) . Hermite polynomials are polynomials defined in the rang of (-∞,+∞). They can be obtained by using the recursive formula:

$H_{n+1}(x)=2xH_{n}(x)-H_{n}'(x).$

with initial values:

$H_{0}(x)=1\,$

$H_{1}(x)=2x\,$

The first six probabilists' Hermite polynomials He_n(x).

Hermite polynomials are not orthogonal in general, but can be modified to be orthogonal and cover the whole space by multiplying them with an exponential factor as below:

$\psi _{n}(x)=\left(2^{n}n!{\sqrt {\pi }}\right)^{-{\frac {1}{2}}}e^{-{\frac {x^{2}}{2}}}H_{n}(x)=(-1)^{n}\left(2^{n}n!{\sqrt {\pi }}\right)^{-{\frac {1}{2}}}e^{\frac {x^{2}}{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}~.$

Hermite functions 0 (black), 1 (red), 2 (blue), 3 (yellow), 4 (green), and 5 (magenta).

Finally, an ECG beat, x(t), can be approximated and modelled as below:

$x(t)=sum_{n=0}^{N}-1a_{n}\psi _{n}(x),$

where the :$a_{n}$ are the coefficients of the linear combination and the :$\psi _{n}(x)$ are the Hermitian basis functions.
More information regarding Hermite basis functions is outside of the scope of my project but if you are interested please click here.

Gaussian

Normalized Gaussian curves with expected value μ and variance σ². The corresponding parameters are $a={\tfrac {1}{\sigma {\sqrt {2\pi }}}}$, b = μ, and c = σ.

In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form:

$f\left(x\right)=ae^{-{\frac {(x-b)^{2}}{2c^{2}}}}$

More information regarding Gaussian functions is outside of the scope of my project but if you are interested please click here.

Method

Classification Methods

When the calculation of parameters of the model for each interval is over, the feature vectors were generated for each ECG beat. To classify the feature vectors I will use 3 different classification methods and compare their rate of success. These methods are k-Nearest Neighbours (k-NN), Neural Networks and multinomial logistic regression.

k-Nearest Neighbors (k-NN)

In pattern recognition, the k-Nearest Neighbors algorithm (or k-NN for short) is a Non-parametric statistics classification and regression analysis. In both cases, the input consists of the k closest training examples in the feature space. The output depends on whether k-NN is used for classification or regression:

• In k-NN classification, the output is a class membership. An object is classified by a majority vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of that single nearest neighbor.

• In k-NN regression, the output is the property value for the object. This value is the average of the values of its k nearest neighbors.

k-NN is a type of instance-based learning, or lazy learning, where the function is only approximated locally and all computation is deferred until classification. The k-NN algorithm is among the simplest of all machine learning algorithms.

Both for classification and regression, it can be useful to assign weight to the contributions of the neighbors, so that the nearer neighbors contribute more to the average than the more distant ones. For example, a common weighting scheme consists in giving each neighbor a weight of 1/d, where d is the distance to the neighbor.

The neighbors are taken from a set of objects for which the class (for k-NN classification) or the object property value (for k-NN regression) is known. This can be thought of as the training set for the algorithm, though no explicit training step is required. This short description of the k-NN algorithm was taken from Wikipedia, if you are interested to know more about k-NN algorithm please click here.
For my project I used the simplest version of k-NN which is 1NN due to simplicity, time complexity and good results achieved by it, as well as 3-NN (which yielded lower accuracy results, as well as adding more complexity to the computations). The k-NN classifier separates various forms of ECG beats according to the following steps:

• Identification of k nearest neighbors out of N training vectors, irrespective of class labels.
  
• Identification of the number of vectors, k_i, that belong to a certain class of arrhythmia among all the k samples.
  
• Assignment of the input sample x to a certain arrhythmia class with the maximum number k_i of samples.
  

Different distance measures are suggested for the determination of the nearest neighbors. I used the Euclidean distance for this project due to simplicity.

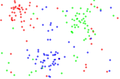
• Example of an arbitrary data set and the corresponding 1NN and 5NN Classification maps
• 

  Fig. 1. The dataset.

• 

  Fig. 2. The 1NN classification map.

• 

  Fig. 3. The 5NN classification map.

Neural Networks

Another classification method that I used is neural networks. After remodelling of the ECG beat signals and generation of the new feature vector, I utilized the neural network method to classify the five types of heart arrhythmia. A fully connected Neural Network with 3 hidden layers was used in this experiment. In the network architecture 64, 32 and 16 neurons were used in hidden layers respectively with an additional bias node. Hyperbolic tangent activation function for each neuron and softmaxLoss after the last layer were utilized in the network. Back propagation method which benefit from momentum and weight decay parameters was used in training phase. The results achieved by neural networks are less accurate when comparing with the 1-NN technique which is due to small training size. On the other hand, neural networks method is significantly faster than k-NN and are more scalable. The results will be further analyzed in the discussion section.
For information about Neural Networks please visit our Wiki page, and for more information regarding statistical classification via various methods such as neural network please click here.

Multinomial Logistic Regression

Lastly, the structure of my data suggests using Multinomial Logistic model to predict different types of heart arrhythmia based on signal features. As I mentioned above, the 5 types of arrhythmia can be predicted by a multinomial logistic regression as well. I consider 2 models based on logistic regression in this project: simple multinomial logistic model, and logistic model with L2-regularization. Since there are too many signal features, regularization can help us to eliminate unnecessary features from the prediction model by penalizing the coefficients. I compare the prediction accuracy of these models with other suggested methods in the discussion session.

Evaluation

All the evaluation will be based on the 9367 ECG beats in five types. 60% (5618) of the beats were used to train, 20% (1874) were used to validate and 20% (1874) were used to test.
Number of train and test beats of each type of ECG beats is given in the table below:

Beat Type	Total # of beats	# of Train beats	# of Validation beats	# of Test beats
N	2000	1200	400	400
PVC	2938	1760	589	589
APC	722	434	144	144
RBBB	2250	1350	450	450
LBBB	1456	874	291	291

Where N, PVC, APC, RBBB and LBBB are the 5 types of arrhythmias as mentioned before. Next is to define the Accuracy, Sensitivity and Specificity as:

${\begin{aligned}{\text{Accuracy}}&={\frac {{\text{number of true positives}}+{\text{number of true negatives}}}{{\text{number of true positives}}+{\text{number of true negatives}}+{\text{number of false positives}}+{\text{number of false negatives}}}}\\\\\end{aligned}}$

${\begin{aligned}{\text{Sensitivity}}&={\frac {\text{number of true positives}}{{\text{number of true positives}}+{\text{number of false negatives}}}}\\\\\end{aligned}}$

${\begin{aligned}{\text{Specificity}}&={\frac {\text{number of true negatives}}{{\text{number of true negatives}}+{\text{number of false positives}}}}\\\\\end{aligned}}$

Results

The results of classification of five types of arrhythmias using the 1-NN, 3-NN, neural networks, simple multinomial logistic regression and multinomial logistic regression with L2-regularization classification methods both after and before remodelling of the signals are illustrated in the figures below:

Conclusion

The achieved results of classification of five types of morphological heart arrhythmias indicate that the suggested methods can obtain almost expert human-level accuracy. The ability of Hermitian basis function to reduce the size of the feature vector is an important matter and significantly helped the improvement of the process both in terms of results and complexity. This size reduction significantly reduced the volume of the needed data to be stored. Moreover, this reduction method can be used in other applications of signals, such as ECG beat signal compression that would require only small parameters to represent and model the original ECG beat.
The results of the k-NN classifiers are significantly better than the signal form. In the neural network approach, the network learns to decrease the weights of unimportant elements in the feature vector. The results of signal is better in this case, due to possessing more details. In terms of computation time, neural nets are significantly faster than k-NN methods where we have to calculate the Euclidean distance of all training set for each test input which is extremely time consuming. The accuracy of the neural network can be scaled with larger data set and that is the main point of improvement for my neural network method. I ran two types of multinomial logistic model (simple, and L2-regularization) for each set of features (signal, and model) to compare the prediction accuracy of my logistic regression models for this dataset and find the best model. By comparing the results i found that among logistics models the multinomial logistic model with L2-regularization for model has the highest accuracy, so it seems to be the best model in the category of logistic models. On the other hand, the simple multinomial logistic model for signal has the least prediction accuracy. I expected to find these results, because adding L2-regularization to my model can lead to more precise prediction. In terms of computational cost, the logistic models for signals have the worst performance and it takes too much time to find the estimates of coefficients for these models. Converting the signal features to new features based on the model can significantly improve the computational performance of my models.
The main strength of the experiment is the comparison of various methods of classification with comparable expert human-level accuracy which can be used an automatic computer assisted diagnosis (CAD) system, while one weakness of the work is its unbalanced data set, meaning I do not possess equal number of data for all the classes of arrhythmia. The latter can be improved by using more amount of balanced data.

Future Work

• Coverage and exploration of other morphological heart arrhythmia
• Performing the algorithms on larger data sets
• Dealing with the white [white gaussian noise definition Gaussian noise]
• Make the model more stable and less sensitive to outliers
• Exploring and analyzing other classification algorithms

Other Classifier Alternatives

Other classifiers that can be explored and investigated to improve the task are:

• Support Vector Machines (SVMs)
  
• Naive Bayes
  
• Decision Trees
  
• Random Forests
  

To Add

A starting point for anyone who wants to participate on this project or contribute to this Wiki page can be exploration and investigation of other Classification methods. As well as, classifying other types of arrhythmias using this framework.