Vision Transformers (ViT)

Vision Transformers

Vision Transformers are a type of deep neural network architecture that uses self-attention mechanisms to process visual data in a manner similar to how humans perceive the world.

Principal Author: Anubhav Garg

Abstract

Vision Transformers are a recent breakthrough in the field of computer vision, bringing the success of the transformer architecture in natural language processing to image and video analysis. These models use self-attention mechanisms to dynamically weigh the importance of different regions in an input, allowing them to process and understand visual data in a manner that is similar to how humans perceive the world. This is similar to how humans perceive the world, as we don't simply focus on a single point of an image or scene, but rather take in multiple elements and features at once. These models have shown remarkable results in a wide range of tasks, from image classification and object detection to image segmentation and video analysis, surpassing previous state-of-the-art results by a large margin. The simplicity of the architecture, as well as the ability to fine-tune on large datasets, has made Vision Transformers a popular choice for a wide range of computer vision applications, and the field is rapidly evolving, with ongoing research exploring new architectures, training strategies, and applications. We will cover working and architectures of these below.

Builds on

Initial work on ViT is build on this paper. Prior to ViTs, vision based tasks such as image classification, segmentation and object recognition were done using convolutional neural networks.

Related Pages

Transformers are an advanced neural networks, first used in the field of natural language processing which was introduced in Attention is All you Need paper. An interesting reading for attention is here. The writing here is also inspired by [3].

Content

The Visual Transformer (ViT) architecture is built on the transformer architecture, which was originally designed for text-based tasks. ViT follows a similar approach as transformers, where it represents an input image as a sequence of image patches that are used to predict the class labels directly. ViT has achieved exceptional performance when trained on adequate amounts of data, outperforming a similar state-of-the-art Convolutional Neural Network (CNN) while using only a quarter of the computational resources. To represent images, ViT divides the input image into fixed-size patches and adds positional embeddings to the transformer encoder, unlike CNNs, which use pixel arrays. This method allows ViT to embed information globally across the image and learn the relative location of image patches, which helps to reconstruct the structure of the image. ViT's self-attention layer plays an essential role in this process. Furthermore, ViT models are approximately four times more efficient and accurate than CNNs. Unlike the standard transformer architecture, which accepts a 1D sequence of token embeddings as input, ViT transforms images into a sequence of visual tokens.To handle 2D images, the image $x\in R^{H\times W\times C}$ is reshaped into a sequence of flattened 2D patches $x_{p}\in \mathbb {R} ^{N\times (P^{2}\cdot C)}$, where (H, W) is the resolution of the original image, C is the number of channels, (P, P) is the resolution of each image patch, and $N={\frac {H\cdot W}{P^{2}}}$ is the resulting number of patches, which also serves as the effective input sequence length for the Transformer. Therefore, if the image is of size 48 by 48 and the patch size is 16 by 16, then there will be 9 patches for the image. The Transformer uses constant latent vector size D through all of its layers, so the patches are flattened and mapped to D dimensions with a trainable linear projection. The output of this projection is referred to as the patch embeddings.

To represent an image, each patch is converted into a 1D patch embedding by concatenating all pixel channels and then projecting it linearly to the desired input dimension. To retain positional information, the patch embeddings are augmented with position embeddings. Transformers do not depend on the arrangement of input elements. By incorporating learnable position embeddings to each patch, the model can acquire knowledge about the image's structure.

To represent an image, we insert an additional learnable classification token at the beginning of the sequence of patch embeddings. The purpose of the classification token is to act as an embedding of a virtual "class" that corresponds to the image. During training, the model is trained to attend to the "classification token" to predict the correct image class. The sequence of patch embedding vectors, including the classification token, serves as the input sequence length for the Transformer Encoder.

The self-attention operation incurs a quadratic cost. If we feed each pixel of the image as input, then each pixel must attend to every other pixel, making the cost of self-attention very high and unable to scale to realistic input sizes. As a result, the image is split into patches to avoid the quadratic cost of self-attention.

ViT architecture

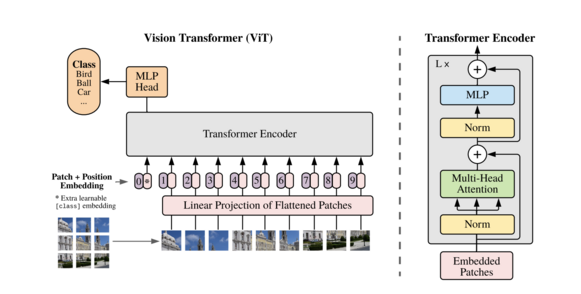
The transformer encoder includes:

• Multi-Head Self Attention Layer (MSAL) : This layer works by computing a set of attention scores between every pair of patch embeddings, using learned parameters to determine the importance of each patch with respect to the others. The attention scores are used to compute a weighted sum of the patch embeddings, where the weights reflect the importance of each patch. By using multiple attention heads, the MSAL can capture both local and global dependencies in an image.

• Multi-Layer Perceptrons (MLP) Layer: This layer contains a two-layer with Gaussian Error Linear Unit (GELU). MLP layer with GELU activation is applied to each patch embedding separately. The output of the MLP layer is then added to the input patch embedding, resulting in an updated patch embedding that has been transformed by the MLP layer. This process is repeated for all patch embeddings in the image sequence, and the resulting sequence of updated patch embeddings is passed on to the next layer of the transformer.

• Layer Norm (LN): The purpose of LN is to normalize the inputs to each layer to have zero mean and unit variance, which can help with the convergence of the training process and improve the overall performance of the model.

ViTs have shown impressive performance with reduced computational resources for pre-training when compared to CNNs. However, on smaller datasets, ViTs inductive bias is generally weaker than that of CNNs, which means it relies more on data augmentation or model regularization.

Inductive bias

Compared to CNNs, ViTs has a weaker inductive bias that is specific to images. In CNNs, every layer of the model has built-in locality, two-dimensional neighborhood structure, and translation equivariance. On the other hand, ViT only has MLP layers that are local and translationally equivariant, while the self-attention layers are global. ViT utilizes the two-dimensional neighborhood structure only in the beginning of the model by dividing the image into patches and during fine-tuning to adjust the position embeddings for images with different resolutions. Apart from these uses, the position embeddings at initialization time do not provide information about the 2D positions of the patches. As a result, the model must learn all spatial relations between the patches from scratch.

Example through code

The below example is inspired from [2] and explained by me. We will first start by importing some libraries.

import matplotlib.pyplot as plt
from PIL import Image

import torch
import torch.nn.functional as F
from torch import Tensor, nn
from torchsummary import summary
from torchvision.transforms import Compose, Resize, ToTensor

from einops import rearrange, reduce, repeat
from einops.layers.torch import Rearrange, Reduce

transform = Compose([
    Resize((224, 224)),
    ToTensor(),
])

x = transform(img)
x = x.unsqueeze(0)
print(x.shape)

Next, we have to break the image into multiple patches, and flatten them. This is achieved by concatenating all the pixel channels in the patch and then linearly projecting them to the desired input dimension. Flattening the patches in this way transforms the pixel values of each patch into a single vector, which can then be passed through the model's Transformer encoder.

Position embeddings are then added to the patch embeddings to retain positional information. Standard learnable 1D position embeddings are used.

PatchEmbedding:
    Initialize:
        patch_size = given_patch_size
        super().__init__()
        projection = nn.Sequential(
            nn.Conv2d(in_channels, emb_size, kernel_size=patch_size, stride=patch_size),
            Rearrange('b e (h) (w) -> b (h w) e')
        )
        cls_token = nn.Parameter(torch.randn(1,1, emb_size))
        positions = nn.Parameter(torch.randn((img_size // patch_size) **2 + 1, emb_size))

    Define forward function that takes input tensor x:
        b, _, _, _ = shape(x)
        x = projection(x)
        cls_tokens = repeat(cls_token, '() n e -> b n e', b=b)
        x = torch.cat([cls_tokens, x], dim=1)
        x += positions
        return x

The resulting sequence of embedding vectors serves as input to the encoder. The TransformerEncoder module applies a stack of depth Transformer encoder blocks to the sequence of patches to extract features and model dependencies between the patches.

TransformerEncoderBlock:
    Initialize:
        emb_size = given_emb_size
        drop_p = given_drop_p
        forward_expansion = given_forward_expansion
        forward_drop_p = given_forward_drop_p
        
        super().__init__(
            ResidualAdd(nn.Sequential(
                nn.LayerNorm(emb_size),
                MultiHeadAttention(emb_size, **kwargs),
                nn.Dropout(drop_p)
            )),
            ResidualAdd(nn.Sequential(
                nn.LayerNorm(emb_size),
                FeedForwardBlock(
                    emb_size, L=forward_expansion, drop_p=forward_drop_p),
                nn.Dropout(drop_p)
            )
            ))

In our implementation, a multi-head attention mechanism will be utilized. This approach involves splitting the computation across several attention heads, each of which focuses on a different part of the input. By dividing the input in this way, the computation becomes more efficient, as the attention mechanism is applied to smaller, more manageable input sizes. Additionally, this strategy enables the model to attend to various aspects of the input, allowing it to capture more complex relationships and dependencies between different elements.

MultiHeadAttention:
    Initialize:
        emb_size = given_emb_size
        num_heads = given_num_heads
        dropout = given_dropout
        
        super().__init__()
        self.qkv = nn.Linear(emb_size, emb_size * 3) # queries, keys and values matrix
        self.att_drop = nn.Dropout(dropout)
        self.projection = nn.Linear(emb_size, emb_size)
    
    Forward(self, x: Tensor, mask: Tensor = None) -> Tensor:
        # split keys, queries and values in num_heads
        qkv = split(self.qkv(x), num_splits = 3) # returns a tuple with 3 tensors
        queries, keys, values = qkv[0], qkv[1], qkv[2]
        queries = rearrange(queries, "b n (h d) -> b h n d", h=num_heads)
        keys = rearrange(keys, "b n (h d) -> b h n d", h=num_heads)
        values = rearrange(values, "b n (h d) -> b h n d", h=num_heads)
        
        # sum up over the last axis
        energy = matmul(queries, transpose(keys, perm=[0, 1, 3, 2])) # batch, num_heads, query_len, key_len
        
        if mask is not None:
            fill_value = min_float_value # set minimum float value for filling the mask
            energy.mask_fill(~mask, fill_value)
            
        scaling = sqrt(emb_size)
        
        att = softmax(energy, dim=-1) / scaling
        att = self.att_drop(att)
        out = matmul(att, values) # sum over the third axis
        out = rearrange(out, "b h n d -> b n (h d)")
        out = self.projection(out)
        
        return out

Before tide everything up, we need the last bit — the classification head. This block, after computing a simple mean over the whole sequence, is a standard fully connected which gives the class probability.

class ClassificationHead(nn.Sequential):
    def __init__(self, emb_size: int = 768, n_classes: int = 1000):
        super().__init__(
            Reduce('b n e -> b e', reduction='mean'),  # Average across sequence length
            nn.LayerNorm(emb_size),  # Normalize features
            nn.Linear(emb_size, n_classes)  # Linear layer to output class scores
        )

The ClassificationHead class takes in a emb_size parameter which is the size of the input embedding, and a n_classes parameter which is the number of output classes. It inherits from the nn.Sequential class and consists of three sequential layers:

Reduce('b n e -> b e', reduction='mean'): This layer averages the input sequence along the sequence length dimension (n) to produce a single feature vector for each example in the batch (b). nn.LayerNorm(emb_size): This layer normalizes the feature vectors using Layer Normalization as was explained in the Content section. nn.Linear(emb_size, n_classes): This layer performs a linear transformation on the normalized feature vectors to produce class scores for each example in the batch.

By composing everything we built so far, we can finally build the ViT architecture.

class ViT(nn.Sequential):
  
    def __init__(self,     
                in_channels: int = 3,
                patch_size: int = 16,
                emb_size: int = 768,
                img_size: int = 224,
                depth: int = 12,
                n_classes: int = 1000,
                **kwargs):
        # Initialize Sequential model
        super().__init__(
            # Add PatchEmbedding layer with given parameters
            PatchEmbedding(in_channels, patch_size, emb_size, img_size),
            # Add TransformerEncoder layer with given depth and emb_size
            TransformerEncoder(depth, emb_size=emb_size, **kwargs),
            # Add ClassificationHead layer with given emb_size and n_classes
            ClassificationHead(emb_size, n_classes)
        )

The ViT module takes several hyperparameters as input, including the input image size (img_size), the number of channels in the input image (in_channels), the size of each patch (patch_size), the embedding size (emb_size), the number of encoder layers (depth), and the number of output classes (n_classes).

Do try it yourself!

Conclusion

In conclusion, the Vision Transformer, a variant of the Transformer architecture, has emerged as a highly effective solution for various computer vision tasks, including image classification, object detection, and semantic segmentation. The unique structure of the Transformer, with its self-attention mechanism, enables it to effectively handle the large input size and spatial dependencies in visual data. The remarkable performance of the ViTs has led to its widespread adoption in the computer vision community and has paved the way for new and exciting research in this field. With the continued advancement of deep learning techniques, it is likely that the ViTs will continue to play a significant role in shaping the future of computer vision.

Annotated Bibliography

[1] Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., & Houlsby, N. (2020). An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. ArXiv. https://doi.org/10.48550/arXiv.2010.11929

[2] https://github.com/FrancescoSaverioZuppichini/ViT

[3] https://viso.ai/deep-learning/vision-transformer-vit/