In short, the Fourier convergence theorem states the following.
If  is a periodic function such that is a periodic function such that  and and  are piecewise continuous, then the Fouriner series converges to are piecewise continuous, then the Fouriner series converges to  at all points where at all points where  is continuous and converges to is continuous and converges to ![{\displaystyle {\frac {1}{2}}[f(x+)+f(x-)]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/ed90fb492f4e27ef2ea6c4ec9ebe8a1ecdd9a52c) at all points where at all points where  is discontinuous. is discontinuous. |
In the above,  denotes the right hand limit of
denotes the right hand limit of  at
at  , while
, while  denotes the left hand limit of
denotes the left hand limit of  at
at  . In other words, for a real number
. In other words, for a real number  ,
,

With the Fourier convergence theorem in mind, let's find out the point of convergence of the Fourier cosine series  at each point
at each point  in the interval
in the interval ![{\displaystyle [0,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) . To do so, we first need to understand the origin of the Fourier cosine series. Recall that the Fourier cosine series is the Fourier series of
. To do so, we first need to understand the origin of the Fourier cosine series. Recall that the Fourier cosine series is the Fourier series of  where
where  is the even extension of
is the even extension of  . Following the Fourier convergence theorem, to find the point of convergence of the Fourier cosine series, we need to know where the points of continuity and discontinuity of
. Following the Fourier convergence theorem, to find the point of convergence of the Fourier cosine series, we need to know where the points of continuity and discontinuity of  are. We will do so by sketching the graph of
are. We will do so by sketching the graph of  . To begin, we sketch the graph of
. To begin, we sketch the graph of  .
.
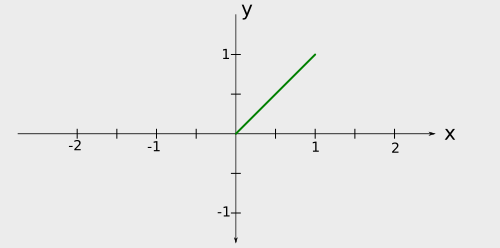
A sketch of

The graph of  is obtained by first reflecting
is obtained by first reflecting  over the y-axis and hence obtaining a function over the interval
over the y-axis and hence obtaining a function over the interval ![{\displaystyle [-1,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) .
We then periodic extend this function to get
.
We then periodic extend this function to get  which will have a period of
which will have a period of  .
.
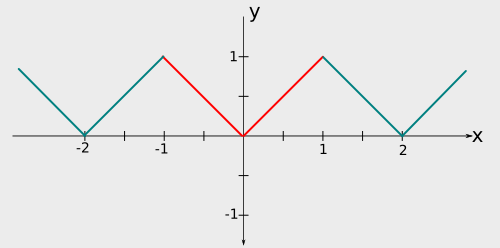
A sketch of the even extension of

. The part of the function from

to

is coloured in red. The red part shows one period of

.
From the sketch of  , we see that
, we see that  is continuous everywhere. Hence, by the Fourier convergence theorem, the Fourier cosine series
is continuous everywhere. Hence, by the Fourier convergence theorem, the Fourier cosine series  converges to
converges to  for every real number
for every real number  . Now, since
. Now, since  agrees with
agrees with  at every point in the interval
at every point in the interval ![{\displaystyle [0,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) ,
,
 converges to
converges to  at every point
at every point  in the interval
in the interval ![{\displaystyle [0,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d) .
.
Similarly, let  be the odd extension of
be the odd extension of  . Then the Fourier sine series
. Then the Fourier sine series  is the Fourier series of
is the Fourier series of  . We will sketch
. We will sketch  to find its points of continuity and discontinuity.
to find its points of continuity and discontinuity.
The graph of  is obtained by first rotating
is obtained by first rotating  about the origin by 180 degree and hence obtaining a function over the interval
about the origin by 180 degree and hence obtaining a function over the interval ![{\displaystyle [-1,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) . We then periodic extend this function to get
. We then periodic extend this function to get  which will have a period of
which will have a period of  .
.
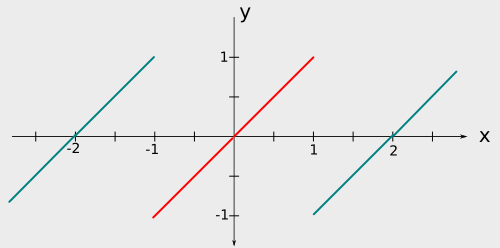
A sketch of the odd extension of

. The part of the function from

to

is coloured in red. The red part shows one period of

.The values at points of discontinuity is not specified in the sketch.
From the sketch of  is discontinuous at points
is discontinuous at points  with k an integer. Hence, by the Fourier convergence theorem, the Fourier sine series
with k an integer. Hence, by the Fourier convergence theorem, the Fourier sine series  converges to
converges to  at every point in the interval
at every point in the interval  , but at
, but at  ,
,  converges to
converges to
![{\displaystyle {\frac {1}{2}}[f_{\text{odd}}(1-)+f_{\text{odd}}(1+)]={\frac {1}{2}}[1+(-1)]=0}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/e5be62c931e1c3a72d0dea65bd3c3597ff12c637) .
.
Since  agrees with
agrees with  in the interval
in the interval  ,
,
-
 converges to
converges to  at every point in the interval
at every point in the interval  and at
and at  ,
,  converges to 0.
converges to 0.
Finally, the question asks us to verify our conclusions for the Fourier sine series at x = 0 and x = 1. Evaluate the sine series found at part a at  , we get
, we get

and evaluating at  , we get
, we get

as expected.



![{\displaystyle {\frac {1}{2}}[f(x+)+f(x-)]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/ed90fb492f4e27ef2ea6c4ec9ebe8a1ecdd9a52c)






![{\displaystyle [0,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


![{\displaystyle [-1,1]}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)







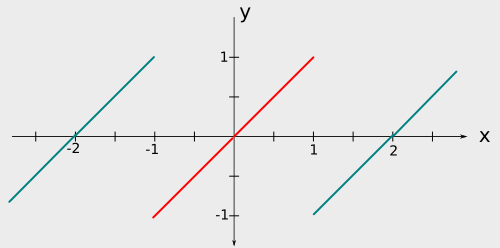




![{\displaystyle {\frac {1}{2}}[f_{\text{odd}}(1-)+f_{\text{odd}}(1+)]={\frac {1}{2}}[1+(-1)]=0}](https://wiki.ubc.ca/api/rest_v1/media/math/render/svg/e5be62c931e1c3a72d0dea65bd3c3597ff12c637)




