Science:Math Exam Resources/Courses/MATH215/December 2013/Question 05 (a)/Solution 1

We begin by finding the eigenvalues and eigenvectors.

The characteristic polynomial of ${\begin{bmatrix}0&3\\2&1\end{bmatrix}}$ is $\lambda ^{2}-\lambda -6=(\lambda -3)(\lambda +2)$ which has roots $\lambda =3,-2$. The find the eigenvector with eigenvalue $\lambda$, we seek the nullspace of $A-\lambda I$.

With $\lambda =3$, we have:

${\begin{bmatrix}-3&3\\2&-2\end{bmatrix}}{\vec {v}}={\vec {0}}.$

From the equation implied by the first row (the second is redundant), $-3v_{1}+3v_{2}=0$ so we can take ${\vec {v}}=\langle 1,1\rangle$.

With $\lambda =-2$, we have:

${\begin{bmatrix}2&3\\2&3\end{bmatrix}}{\vec {v}}={\vec {0}}$.

From the equation implied by the first row (the second is the same), $2v_{1}+3v_{2}=0$ so we can take ${\vec {v}}=\langle 3,-2\rangle$ as an eigenvector.

The general solution is ${\vec {x}}(t)=C_{1}{\begin{bmatrix}1\\1\end{bmatrix}}e^{3t}+C_{2}{\begin{bmatrix}3\\-2\end{bmatrix}}e^{-2t}$.

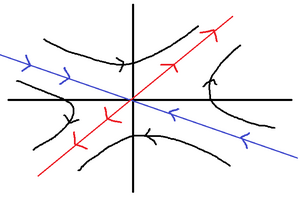
The origin is a saddle point because the eigenvalues are real and of opposite sign. Along the $\displaystyle \langle 1,1\rangle$ direction, the solution grows exponentially. Along the $\displaystyle \langle 3,-2\rangle$ direction, the solution decays exponentially. At all other points, it will approach the line spanned by $\displaystyle \langle 1,1\rangle$ as $t\rightarrow \infty$. This is displayed in the figure.