Science:Math Exam Resources/Courses/MATH102/December 2011/Question 04 (vi)/Solution 1

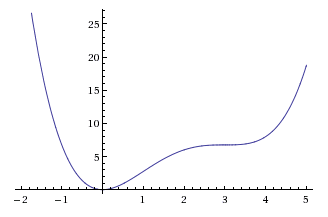
This function is a polynomial of degree 4, so the curve sketching shouldn't offer too many difficulties. We have collected the following information:

• The function has no horizontal asymptotes (from part i) )
• The function has a global minimum at x = 0 (from part ii) )
• The function has two inflection points at x = 1 and x = 3 (from part iii) )
• The function is decreasing up to its minimum and then increasing, except at x = 3 where it has an inflexion point (from part iv) )
• The function is concave up all the way up to x = 1, then concave down until x = 3 and then concave up again (from part v) )

To get a better idea of what to sketch, we quickly compute the second coordinates of the three points of interests:

• Global minimum at (0,0)
• Inflection points at (1, 11/4) and (3, 27/4)

This allows us to sketch the graph of this function. As we saw above, this function is always positive, reaches a global minimum at the point (0,0) and has two inflection points. This should give you a picture that looks like: