Science:Math Exam Resources/Courses/MATH101/April 2010/Question 06/Solution 1

There is a certain ambiguity to how the diagram presents this problem. While it talks of a standard swimming pool with an inclined plane along the bottom, the diagram looks as if the top-side is inclined. Therefore we will present a solution where the bottom is flat and the top side is inclined and another solution where the top is flat and the bottom side is inclined. The approach to both problems is the same but the numerical results will differ.

Top Inclined, Bottom Flat:

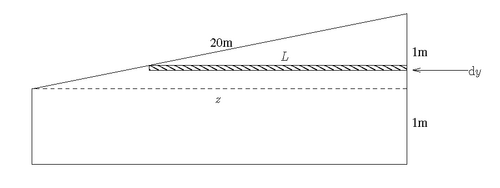
Create a diagram (like that to the right) that just illustrates the side of pool we are interested in

. We will use the standard coordinate system of $x$ representing the horizontal direction and $y$ representing the vertical direction.

Notice we can divide the figure into a rectangular portion and a triangular portion which in the diagram is separated by a dashed line. Since this triangular portion is actually a right triangle we can determine the missing size $z$ to be

$z={\sqrt {20^{2}-1^{2}}}={\sqrt {399}}.$

Now we are interested in determining the hydrostatic force that is exerted on this pool wall. From the hint we know this depends on the pressure which we can write as,

$\displaystyle {}P=\rho {}g(2-y)$

where we take $y=0$ to be the bottom of the diagram. Notice that because of this definition of y, the depth, h, as defined in the hint is then actually h=2-y since the top of the surface is at y=2. We see that depending where we are along the pool side, we will exert a different pressure and therefore a different force. Since the pressure depends on $y$, let's consider a very small rectangle of height ${\textrm {d}}y$ and length, $L$. The small amount of force exerted on this rectangle of area ${\textrm {d}}A$ is,

$\displaystyle {}{\textrm {d}}F=P{\textrm {d}}A=\rho {}g(2-y)Ldy.$

Therefore the total amount of force exerted will be the sum of the little amounts of force on each rectangle as we go from height $y=0$ to height $y=2$. However, we have to be careful, because as we climb up the height of the pool side, the length of the small rectangles depend on our height $y$ due to the pool getting narrower in the triangular region. We will then break up the problem into computing the total force on the rectangular portion, $F_{1}$ and the total force on the triangular portion, $F_{2}$. In the end the total force will be, $F=F_{1}+F_{2}$.

Rectangular Portion:

In this region, for any given height, $y$, the length is a constant and in fact we already computed it,

$L={\sqrt {399}}.$

Therefore, for this region we have that for every little rectangle,

$\displaystyle {\textrm {d}}F_{1}=\rho {g}{\sqrt {399}}(2-y){\textrm {d}}y.$

In order to add up the contributions from all the small rectangles we turn to integration,

${\begin{aligned}F_{1}=\int {\textrm {d}}F_{1}&=\int _{0}^{1}\rho {g}{\sqrt {399}}(2-y){\textrm {d}}y\\&=\rho {g}{\sqrt {399}}\left.\left(2y-{\frac {y^{2}}{2}}\right)\right|_{0}^{1}\\&={\frac {3\rho {g}{\sqrt {399}}}{2}}.\end{aligned}}$

The limits of integration can be seen from the diagram since the rectangular region starts at the bottom and goes up 1m.

Triangular Portion:

This region is slightly more tricky to compute because the length changes with the height. The first thing we need to do is figure out a function for the slanted side of the triangle in terms of $x$ and $y$. We see that it is a line so it will be of the form $y=mx+b$ with $m$ the slope and $b$ the y-intercept. We know that when the height is 1, we are at the left edge of the diagram which we will denote $x=0$. When the height is 2, we are at the right edge of the diagram which we know is

$x={\sqrt {399}}.$

Therefore we get that the slope is

$m={\frac {2-1}{{\sqrt {399}}-0}}={\frac {1}{\sqrt {399}}}$

and the y-intercept occurs when $x=0$ so $b=1$. Therefore, the slanted edge of the triangle is given by,

$y={\frac {1}{\sqrt {399}}}x+1.$

Now at any height, the length of our small rectangle will start at the slant edge,

$x={\sqrt {399}}(y-1)$

and extend to the right edge of the diagram at $x={\sqrt {399}}$. Therefore we have that the length at any given height $y$, is

$L(y)={\sqrt {399}}-{\sqrt {399}}(y-1)={\sqrt {399}}(2-y).$

The small amount of force on any rectangle in this region is,

${\textrm {d}}F_{2}=P{\textrm {d}}A=\rho {g}yL{\textrm {d}}y=\rho {g}{\sqrt {399}}(2-y)(2-y){\textrm {d}}y.$

In order to get the total force on the triangular region we integrate all these little ${\textrm {d}}F_{2}$ over every height in the triangular region. This region starts at $y=1$ and ends at $y=2$. Therefore these are our lower and upper limits of integration respectively. We get for our total force in this region,

${\begin{aligned}F_{2}=\int {\textrm {d}}F_{2}&=\int _{1}^{2}\rho {g}{\sqrt {399}}(2-y)^{2}{\textrm {d}}y\\&=\rho {g}{\sqrt {399}}\int _{1}^{2}(y^{2}-4y+4){\textrm {d}}y\\&=\rho {g}{\sqrt {399}}\left({\frac {y^{3}}{3}}-2y^{2}+4y\right)_{1}^{2}\\&={\frac {1}{3}}\rho {g}{\sqrt {399}}.\end{aligned}}$

We can now compute the total force as,

$F=F_{1}+F_{2}=\rho {g}{\sqrt {399}}\left({\frac {3}{2}}+{\frac {1}{3}}\right)={\frac {11}{6}}\rho {g}{\sqrt {399}}$

which using the numbers provided in the question, $\rho =1000$ and $g=9.8$, we get,

$F\approx {}358883.9N$

which is a very large force but not unsurprising considering the power that water has.

Caution!!

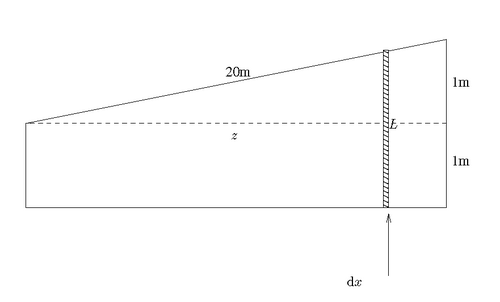
You may be tempted to want to set up an integral with $x$ instead of $y$, i.e. a diagram that looks like that to the right

.

The problem is that, as we mentioned above, the pressure is a function of height. Based on this formulation and this diagram, the small rectangles take every height value from the base of the rectangle to the slanted edge and so the pressure varies along the whole length of the rectangle. You may think that a solution to this problem is to take your rectangle of height, $L$ and width ${\textrm {d}}x$ and splice it up into even smaller rectangles of say height ${\textrm {d}}y$ and width ${\textrm {d}}x$. You then would have an integration problem on your small rectangle from the diagram and then another integration problem as you vary $x$ and look at other small rectangles. This solution technique is very valid and is known as double integration, something that will be covered in more advanced courses.