Science:Math Exam Resources/Courses/MATH101/April 2008/Question 02 (c)/Solution 2

The first step to solve this problem is to understand what volume we are trying to compute.

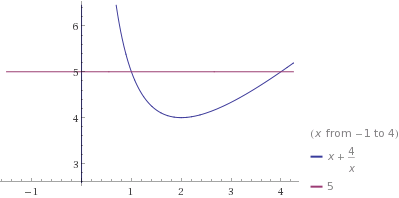
The question states that there is a region delimited by the curves y=5 and y=x+4/x. The second curve looks like the line y=x except that there is a vertical asymptote at x=0. So it seems that it will indeed cross the horizontal line y=5 twice (as it dips down before going back up). We can compute where the intersections are by solving:

$x+{\frac {4}{x}}=5$

which is equivalent to

$\displaystyle x^{2}-5x+4=0$

and has solutions x=1 and x=4. Then we want to know how far down the curve goes, so we look for its local minimum. We compute its derivative:

${\frac {d}{dx}}\left(x+{\frac {4}{x}}\right)=1-{\frac {4}{x^{2}}}$

and hence see that it has two critical points, one at x=-2 and one at x=2. We are only interested in the local minimum which is at x=2. This should be enough details to have you be able to obtain the equivalent of the following picture:

Now we want to rotate this region around the vertical axis x=-1. To do this, we will use the method know as disk integration. The idea is fairly simple: imagine the solid viewed from the top (looking down at the axis), if we slice it along that axis, we will see a slice of a hollow cylinder. We will compute the area of that slice (the difference of area between the outer disk and the inner disk) and integrate.

The outer disc has a radius that starts at the point (2,4) and moves right towards the point (4,5) following the curve y=x+4/x. The inner disc has a radius that starts at the point (2,4) and moves left towards the point (1,5) following the other side of the curve. We need to compute that radius (starting at x=-1). For this, the first step is to express the curve in terms of y instead of x:

${\begin{aligned}y=x+{\frac {4}{x}}&\iff yx=x^{2}+4\\&\iff x^{2}-yx+4=0\\&\iff x={\frac {y\pm {\sqrt {y^{2}-16}}}{2}}\end{aligned}}$

If we look at this, it makes sense: This is only well defined if y is larger than 4 (see on the graph) and there are two components: the one with the + for the right side and the one with the - for the left side. Since the axis of rotation is at x=-1, we need to add 1 to each of the radius and obtain:

${\begin{aligned}r_{outer}(y)&=1+{\frac {y+{\sqrt {y^{2}-16}}}{2}}\\r_{inner}(y)&=1+{\frac {y-{\sqrt {y^{2}-16}}}{2}}\end{aligned}}$

And so we can write the volume by integrating over all the shells, which are obtained by taking the difference of the outer and inner disk:

$V=\int _{4}^{5}\left(\pi \left(1+{\frac {y}{2}}+{\frac {\sqrt {y^{2}-16}}{2}}\right)^{2}-\pi \left(1+{\frac {y}{2}}-{\frac {\sqrt {y^{2}-16}}{2}}\right)^{2}\right)\,dy$

(since the area of a disk of radius r is $\pi$ r²).

Now we can do some algebra to rewrite this integral into something easier to handle. Notice the pattern here

$\displaystyle (A+B)^{2}-(A-B)^{2}=4AB$

Hence we can rewrite this as

${\begin{aligned}V&=\pi \int _{4}^{5}4(1+{\frac {y}{2}})({\frac {\sqrt {y^{2}-16}}{2}})\,dy\\&=\pi \int _{4}^{5}(2+y)({\sqrt {y^{2}-16}})\,dy\\\end{aligned}}$

Now we need to compute that integral to obtain the desired volume. Unfortunately, this won't be straightforward since (2+y) isn't a multiple of the derivative of what is in the square root. There are many ways to compute this integral, here we will split it in 2 and deal with each term.

$V=\pi \int _{4}^{5}2{\sqrt {y^{2}-16}}\,dy+\pi \int _{4}^{5}y{\sqrt {y^{2}-16}}\,dy$

Let us call the first integral V₁ and the second one V₂. The first one is the tougher one. Indeed:

${\begin{aligned}V_{2}&=\pi \int _{4}^{5}y{\sqrt {y^{2}-16}}\,dy\\&={\frac {\pi }{2}}\int _{4}^{5}2y{\sqrt {y^{2}-16}}\,dy\\&={\frac {\pi }{2}}\left[{\frac {2}{3}}(y^{2}-16)^{3/2}\right]_{4}^{5}\\&={\frac {\pi }{2}}{\frac {2}{3}}(25-16)^{3/2}\\&={\frac {\pi }{3}}\cdot 27\\&=9\pi \end{aligned}}$

The first integral is actually quite complicated. At the same time it is a classic. As of today (2012) you are not expected to be able to integrate this by hand and/or know the formula from memory. For completion sake, here is the formula:

$\int {\sqrt {x^{2}-a^{2}}}\,dx={\frac {x}{2}}{\sqrt {x^{2}-a^{2}}}-{\frac {a^{2}}{2}}\ln(x+{\sqrt {x^{2}-a^{2}}})+c$

Which in this case gives us:

${\begin{aligned}V_{1}&=\pi \int _{4}^{5}2{\sqrt {y^{2}-16}}\,dy\\&=2\pi \left[{\frac {y}{2}}{\sqrt {y^{2}-16}}-8\ln(y+{\sqrt {y^{2}-16}})\right]_{4}^{5}\\&=2\pi \left[({\frac {5}{2}}{\sqrt {9}}-8\ln(5+{\sqrt {9}})-(0-8\ln(4+0))\right]\\&=2\pi ({\frac {15}{2}}-8\ln(8)+8\ln(4)\\&=\pi (15-48\ln(2)+32\ln(2))\\&=\pi (15-16\ln(2))\end{aligned}}$

Summing $\displaystyle V=V_{1}+V_{2}$ gives $\displaystyle V=24\pi -16\pi \ln(2)$ which is the same as above.

... This is why using the correct method of solids of revolution is very important.