Motions and Mechanics

This article is part of the PhysicsHelp Tutoring Wiki

The keys to answering questions in mechanics and different motions (1-dimension, multi-dimensional and circular) is to find the right coordination system to work with. A commonly used coordinate system is a Cartesian system with height on the vertical axis and horizontal distance on the other axis. However, sometimes it's useful to define the x-axis along the trajectory of the motion. In multidimensional motion, the axis can be labelled arbitrarily, often depending on which forces act on an object. The forces can be broken down into components along each axis individually and the values of interest can be added as vectors (head to tail) to find the net value. It is equally important to note what type of logical assumptions should be made. Perhaps the most important when dealing with forces and energy is the conservation of energy (i.e. Total energy remains constant). In stationary scenarios, it is important to make general statements such as Fnet = 0 or F (up) = F (down), etc. These statements, although seemingly obvious are the key to truly grasping concepts and problems.

Motions

• Q: A block is sliding down a frictionless inclined plane starting from rest. It makes the whole trip down in 3s. The angle of incline is 30 degrees. What distance does the block cover during these 3s?

• A: The acceleration along the plane is $a=g\sin(t)$, where $t$ is the angle. We can use the formula

$x=ut+{\frac {1}{2}}at^{2}$

where $u=0$ is the initial velocity, $t=3s$, $a=g\sin(t)$. The answer is $22.1m$

• Q: A glider 8cm long blocks light as it goes through a photocell gate. The glider is released from rest on an inclined air track and the gate is positioned so that the glider has traveled $96cm$ when it is in the middle of the gate. The timer gives a reading of $333ms$ for the glider to pass through the gate. Friction is negligible. What is the acceleration of the glider along the track?

• A: The speed of the glider as it passes through the gate is

$v={\frac {d}{t}}={\frac {8cm}{0.333s}}=24cm/s$

which is the velocity at $d=96cm$. The initial velocity, $u=0$. We use the formula $v^{2}=u^{2}+2ax$. That is,

$a={\frac {v^{2}}{2x}}={\frac {(24cm/s)^{2}}{2(96cm)}}=3cm/s^{2}$.

Circular Motion

• Q: A car is traveling at a constant speed of $45km/h$ clockwise around a circular track $1km$ in diameter. In going from the eastern-most point of the track to the western-most point of the track, what is the average velocity of the car?

• A: Remember that the average velocity is the displacement (not distance) divided by time. Whereas the distance is the length over which the car actually traveled, the displacement is the distance between the start point and the end point. So if a car travels around a circle, we calculate the distance as the length around the circumference of the circle, while the displacement is straight line from where the car started to where the car ended.

Even though we need to displacement to find the average velocity, we still need the distance to figure out how long it took. We can calculate the distance traveled like so:

${\mathsf {distance}}=({\mathsf {circumference~of~the~circle}})*({\mathsf {fraction~of~circle~traveled}})=(2\pi r)*\left({\frac {1}{2}}\right)={\frac {\left(2\pi (0.5km)\right)}{2}}={\frac {\pi }{2}}km$

Once we have the distance, we can divide by the speed at which the car traveled to find how long it took:

${\mathsf {time}}={\frac {\mathsf {distance}}{\mathsf {speed}}}={\frac {\left({\frac {\pi }{2}}km\right)}{45km/h}}={\frac {\pi }{90}}h$

Now we know how long it took, so we can divide the displacement by that time to find the average velocity:

${\mathsf {average~velocity}}={\frac {({\mathsf {displacement}})}{({\mathsf {time}})}}={\frac {1km}{{\frac {\pi }{90}}h}}={\frac {90}{\pi }}km/h\approx 28.6km/h.$

We're not quite done yet, since a velocity includes a magnitude and a direction, so we observe the that arrow from the start point to the end point of the car points west, so we say the average velocity is $28.6km/h$ west.

Tension

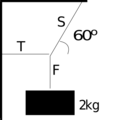
• Q: An object of $2kg$ is being suspended by a set of string that shapes like a Y, with the object attached to the bottom of the Y. One of the top strings is horizontal and it hooked to a nearby wall; where as the other side of Y is hooked up to the ceiling at 60 degree. Find the tension of the horizontal string.

• A: Let the tension of the horizontal string be T, the tension of the string attached to the object be F, and that of the inclined string be S. We know that the tension on the string connected to the object is the force due to gravity, which is proportional to the mass of the object and the acceleration due to gravity:

$F={\mathsf {weight~of~the~object}}={\mathsf {(mass~of~object)}}*{\mathsf {(acceleration~due~to~gravity)}}=mg=(2kg)*(9.81m/s^{2})\approx 1.96N$

Since the system is static (i.e. Not moving), the sum of all the vertical and horizontal forces must be zero. This is a basic assumption appears obvious but is the key statement for many problems. At the intersection of the three strings, therefore, the vertical components of $F$, $S$, $T$ must cancel. So we can write down:

$S*\sin(60)-F=0$

There is no vertical component of T, since it is totally horizontal. Remember that forces pointing in opposite directions have opposite signs.

Next, the horizontal components must add to zero, so we can write:

$S*\cos(60)-T=0$

Now we try to solve for $T$. We can solve the first equation for $S$ in terms of $F$:

$S={\frac {F}{\sin(60)}}\approx 22.6N$

Now that we know S, we can solve the second equation for $T$:

$T={\frac {S}{\cos(60)}}\approx 45.3N$

Moments

Moments can be very challenging and are commonly used by instructors to test whether the student truely understands the principles of what they are learning. It is important to become competent in using a determinent matrix to solve for moments and forces in three dimensions.

Couple Moments

Couple moments can be confusing because they are free vectors. A free vector, in my own words, is a vector that does not depend on it's orientation in space. I think of the vector, up a hundred feet as a free vector because it doesn't refer to its specific spacial coordinates.

Imagine if you could disconnect the steering wheel from a city bus. Now say you have that steering wheel and to its hub (the shaft that connects it to the rest of the bus) you connect a clamp. Then you connect the clamp to a jar of pickles and use the force generated in each hand to twist the lid off. What you've done is use the couple moment, generated by your hands twisting the steering wheel, to torque the jar lid loose. The couple moment you can create with the steering wheel can be applied to anything. It could even be applied to the jar of pickles in another direction. Imagine applying the couple moment to the side of the jar. Now the only result will be to turn the entire jar.

You see, the couple moment is the torque or couple you are generating at a central point. It is not the result that something sees.

• Back to PhysicsHelp