Level Curves

This article is part of the MathHelp Tutoring Wiki

Example 1:
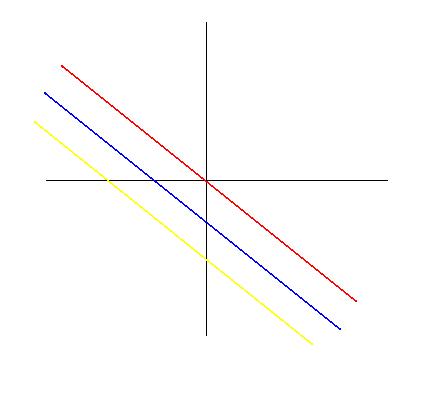
Question: Find the level curves of heights C = -1, 0, 1 for f(x,y) = x+y+1
Solution:

For height C = -1 ( Yellow Line )

f(x,y) = x+y+1 = -1

x+y+1 = -1

y = -2-x

slope = -1

y-intercept = -2

For height C = 0 ( Blue Line )

x+y+1 = 0

y = -1-x

For height C = 1 ( Red Line )

x+y+1 = 1

y = -x

This is the graph that refers to Example 1.

Example 2:
Question: Find the level curves of heights C = 4, 1, 0, and -1 for f(x,y) = $x^{2}+y^{2}$
Solution:

For height C = 4 ( Blue Circle )

$x^{2}+y^{2}=4$

$x^{2}+y^{2}=2^{2}$

For height C = 1 ( Red Circle )

$x^{2}+y^{2}=1$

$x^{2}+y^{2}=1^{2}$

For height C = 0 ( Yellow Dot )

$x^{2}+y^{2}=0$

Only solution is x = 0, y = 0.

For height C = -1

$x^{2}+y^{2}=-1$

Does not exist because $x^{2}+y^{2}$ has to be greater than equal to 0.

This is the graph that refers to Example 2.

• Back to Integral Calculus
• Back to MathHelp