Isotopes Half Life

This article is part of the PhysicsHelp Tutoring Wiki

There have been numerous students asking for help with questions regarding half life. Ive decided to add this page and hopefully make this topic a little simpler.

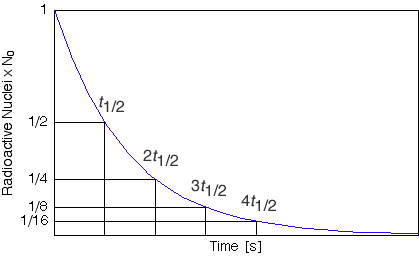
The most important thing to recognize is that for each period of time equal to the half life the amount of radioactive material decreases to a half of the initial amount. It doesn't matter which two points on the graph you consider, if the duration of time between them is equal to one half life the intitial amount will be twice the final amount. Try it out the possabilities are infinite.

N = No (1/2) ^ (t/T)

This is a simple equation that demonstrates the characteristis of half life mathematics well. You can see that exponent of 1/2 is determined by the ration of time duration to half life. As time increase the multiple 1/2 is raised to ever greater powers. For example if you allow a radioactive substance to decay for 8 half lives then the exponent will be eight an therefore,

N = No (1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2) = No (1/256)

And if we used 8.5 half lives,

N = No(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)*((1/2)^0.5) = No(1/156)((1/2)^0.5) = No(1/2)^8.5

As you can see, if the half life has been determined it can be used quite conveniently to determine the amount of radioactive substance remaining. A common application is in the use of radioactive isotopes that are injected into the blood stream to gain visual within the body.

• Back to PhysicsHelp