Image Colourization using Deep Learning

Title

Colourizing grayscale images using deep learning and neural network.

Principal Author: Amin Aghaee

Main papers:

• M. Richart, J. Visca and J. Baliosian, "Image Colorization with Neural Networks," 2017 Workshop of Computer Vision (WVC), Natal, 2017, pp. 55-60.

• Zhang R., Isola P., Efros A.A. (2016) Colorful Image Colorization. In: Leibe B., Matas J., Sebe N., Welling M. (eds) Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science, vol 9907. Springer, Cham

Abstract

This page cover a quick review on two image colourizing algorithms using neural networks for grayscale images. Both algorithms decide the colour of each pixel by looking the texture around that pixel. These algorithms tries different models to decrease number of colour classes to simplify their models.

Builds on

http://wiki.ubc.ca/Course:CPSC522/Convolutional_Neural_Networks

Related Pages

• http://wiki.ubc.ca/Course:CPSC522/Deep_Neural_Network

Content

Introduction

Given a grayscale image, hallucinating a plausible colour version of the photograph has become an interesting question. Nowadays, many graphics experts can convert a grayscale image into a colourful version using graphic tools such as Adobe Photoshop in an hour or less. Choosing reasonable colours for different objects in the images is easier for humans based on our prior knowledge about the colour of objects. For instance, everyone know that the sky is blue or the grass is green. Choosing reasonable colours for computer is a challenging task. However, when it comes to speed, specially in converting grayscale videos (with hundreds of frames) into colourful ones, image colourizing algorithms make more important roles.

Firstly, it is important to find out what is colour and how we can model or present a colour in digital images. Then we introduce two colour spaces and see why the algorithms we are going to look at, choose one specific colour space.

A demo for Colorful Image Colorization algorithm.

Colour Spaces

There are five major colour spaces to model colours in computer, which are: CIE, RGB, YUV, HSL/HSV, and CMYK. The most famous one probably is RGB. But as we will discuss later, learning process using CIE colour spaces is much easier.

RGB Colour Space

RGB (Red, Green, Blue) describes what kind of light needs to be emitted to produce a given colour. Each RGB colour is a 3-byte value <0-255,0-255,0-255> each of which is between 0 and 255 and related to different light channel.

CIELAB

CIELAB is a colour space specified by the International Commission on Illumination (French Commission internationale de l'éclairage, hence its CIE initialism) [1] . The intention of CIELAB (or L*a*b* or Lab) is to produce a colour space that is more perceptually linear than other colour spaces. Perceptually linear means that a change of the same amount in a colour value should produce a change of about the same visual importance. CIELAB has almost entirely replaced an alternative related Lab colour space "Hunter Lab". This space is commonly used for surface colours, but not for mixtures of (transmitted) light. Working with CIELAB has two major advantages in these works: (i) the colour space is designed for perceptual uniformity which makes it ideal for computer processing and (ii) these models only have to predict the a and b channels, as the L channel would be the grey-scale image.

CIELAB color space top view

Colorful Image Colorization

In this work, they train a CNN to map from a grayscale input to a distribution over quantized colour value outputs using the architecture shown in architecture 1. Architectural details and their code are available here, and it is publicly available. CIELAB is discussed earlier. They train this network by giving the Light channel as the training set and predicting a and b channels as their objective.

Architecture 1 : CNN for Colorful Image Colorization algorithm

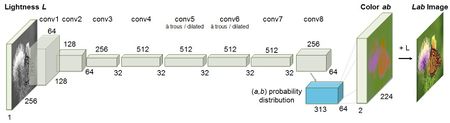
Objective Function

Given an input lightness channel $X\in R^{H\times W\times 1}$, their objective is to learn a mapping ${\hat {Y}}=F(X)$ to the two associated colour channels $Y\in R^{H\times W\times 2}$, where H and W are image dimensions. Another advantage of using CIELAB colour space is that we can model distance with this colour (the expected colour and the predicted one). Because distances in this space model perceptual distance, a natural objective function, is the Euclidean Loss L2 between predicted and ground truth colours:

$L_{2}({\hat {Y}},Y)={\frac {1}{2}}\sum _{h,w}\|Y_{h,w}-{\hat {Y}}_{h,w}\|_{2}^{2}$

However, this loss is not robust to the inherent ambiguity and multimodal nature of the colourization problem. Because of this problem and some other issues, they instead, treat the problem as multinomial classification. So, the output space should have different classes. To do that, they quantize the ab output space into bins with grid size 10 and keep the Q = 313 values which are in-gamut.

Experiment result

In the figure below, you can see the first algorithm full method and comparing the regression and classification outputs.

Experiment result for Colourful Image Colourization algorithm

Image Colourization with Neural Networks

In this work, they also use CIELAB colour space and consider Lightness channel as their training set and a,b channels as their objective. In both works, generating a training dataset is so easy. They just use colourful images in RGB and in pre-processing step, convert those images into CIELAB colour space using other image processing algorithms. Architecture of this paper is different from previous work. They also use one Self Organizing Map method to keep the domain for the predictor small.

Workflow in Image Colourization with Neural Networks

Self Organizing Map (SOM)

A self-organizing map (SOM) or self-organizing feature map (SOFM) is a type of artificial neural network (ANN) that is trained using unsupervised learning to produce a low-dimensional (typically two-dimensional), discretized representation of the input space of the training samples, called a map, and is therefore a method to do dimensionality reduction [2] [3] . Self-organizing maps differ from other artificial neural networks as they apply competitive learning as opposed to error-correction learning (such as back-propagation with gradient descent), and in the sense that they use a neighbourhood function to preserve the topological properties of the input space.

Kohonen Self-Organizing Map demo

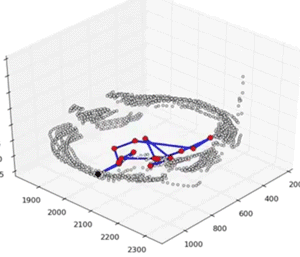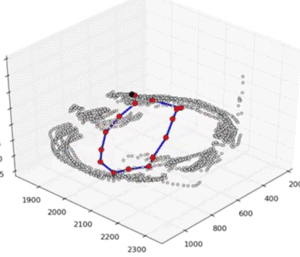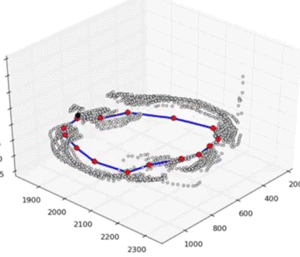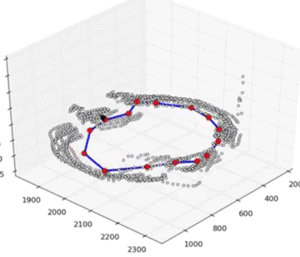
Self-organizing maps are unsupervised methods. They will train SOM before training their CNN on all training images in order to reduce number of classes. So instead of using a large grids over CIELAB colour space (as it's done in previous method), using SOMs, they can reduce label space ($Y$) significantly.

Using SOMs to reduce number of labels in CIELAB images. Comparing the original image with 4-neurones-SOM and 9-neurones-SOM.

Architecture

In this work, a Multi Layer Perceptron (MLP) Neural Network for classification is proposed. The objective of the NN is to classify each patch into the SOM cluster the central pixel belongs to. The input images are breaking into small patches with size $n\times n$ pixels and being flatten into $n^{2}$ input neurones. Number of neurones in the output layer depends on number of neurones in SOM. They try different hidden layer sizes.

Neural Network model for mage Colorization with Neural Networksalgorithm.

They increase number of hidden layers up to 100 and you can see their final result in figure below.

Image Colorization with Neural Networks result.

Annotated Bibliography

M. Richart, J. Visca and J. Baliosian, "Image Colorization with Neural Networks," 2017 Workshop of Computer Vision (WVC), Natal, 2017, pp. 55-60.

Zhang R., Isola P., Efros A.A. (2016) Colorful Image Colorization. In: Leibe B., Matas J., Sebe N., Welling M. (eds) Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science, vol 9907. Springer, Cham

Colour Spaces

T. Kohonen, "The self-organizing map," in Proceedings of the IEEE, vol. 78, no. 9, pp. 1464-1480, Sep 1990.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.