Electrostatics
| This article is part of the PhysicsHelp Tutoring Wiki |
The electric field is a fundamental property of the universe. It is a vector field defined over all of space, which means that at every
point in space it has a value that is a vector with a direction and magnitude. Roughly speaking, this value represents the force per
unit charge that a point charge would experience if placed at that point.
The study of electrostatics is the study of the electric field in situations where charges are no longer permitted to move, or are so small that their motions do not effect the electric field. Eventually you will learn about magnetostatics, which is the study of constant, steady flows of charge in closed loops or long curves, and then if you study physics at a higher level you will learn about electrodynamics, which deals with the generalized interactions between moving charges. For now though, it is useful to learn about the simpler field of electrostatics.
The foundational principle of electrostatics which was derived for experiment from which we can derive all of electrostatics is the definition of the electric field of a point particle of charge at a point a distance from the particle in the direction
We will see how this equation can be used to derive many more interesting properties of electrostatics.
The Principle of Superposition
The most important idea in electrostatics is the principle of superposition. This principle states that if you know the electric field due to a specific configuration of charge and the electric field of some other configuration of charge, then the electric field due to putting both of those configurations on top of each other is simply the sum of the electric fields of each individual configuration.
The simplest possible case where we can use the principle of superposition is to calculate the electrostatic field from a collection of point charges. When drawing out field lines, one should recognize that arrows emanate from positive charges (arrows move AWAY from +q) while arrows point to negative charges. (See below illustration)
Example
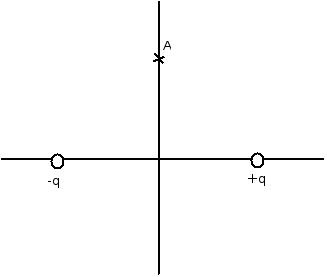
Q:A point charge is located a distance 1 from the origin along the positive x-axis. Another point charge is located a distance 1 from the origin along the negative x-axis. What is the electric field at a distance 1 from the origin along the y-axis (point A in the diagram)?
A:We can calculate the electric field from each individual charge using Coulomb's Law. Then using the principle of superposition, we know that the total electric field is the sum of the field from each
charge.
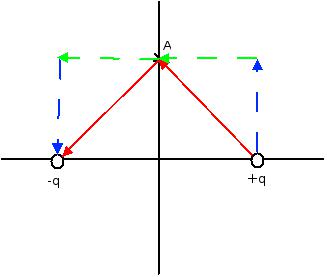
Since point A is a total distance from each charge we use Coulomb's Law:
Where and are the contributions from the positive and negative point charges respectively.
When we add the contributions together we must remember that they are vectors. The value for the electric field at contribution at A from the positive charge is a vector pointing along the direction between the positive charge and A. Since the value is positive, the vector points towards A. The same is true for the contribution from the negative charge, except that it is negative, and thus points away from A. As depicted in the diagram, the vertical components of the vectors cancel each other and the horizontal components add. The result is an electric field vector pointing to the left with magnitude (with ):
Gauss's Law
In principle, we can use the principle of superposition to calculate the electrostatic field of any charge distribution, even solid objects with complicated shapes and some (not necessarily constant) charge density (amount of charge per unit volume). The way this is acheived is by splitting up the object into very small pieces which act alomst like a point charge and then adding their contributions. If we take the limit as the pieces get smaller and smaller, we will get closer and closer to the real value of the electrostatic field. Those who have taken second-term first year calculus may recognize this process as integration. Those who have taken second year calculus will recognize this more specifically as a volume integral.
As you may expect this process is in general very difficult, and Physics 102 you will only need to worry about point charges like in the previous examples. But there exists a special technique for calculating the electric field of more complicated charge distributions more easily in situations with lots of symmetry. This technique uses Gauss's Law.
Gauss's Law is a very general law of electrostatics and is in fact one of the four famous Maxwell Equations, which when taken together desribe the entirely of classical electromagnetism. It is possible to derive Guass's Law from Coulomb's Law, but this requires a complicated calculation which requires integral calculus. It is however very easy to derive Coulomb's Law from Guass's Law, and as a result Guass's Law is usually considered to be more fundamental, even though Coulombs's Law was discovered through experiment.
Guass's Law states that the electric flux through any closed surface is proportional to the net charge enclosed by the surface. More specifically:
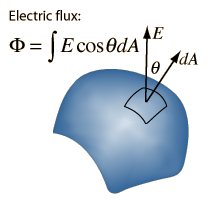
Where this denotes a surface integral. A surface integral consists of splitting a surface into many small, approximately flat and square pieces. For each piece, we define a vector perpendicular to the surface and pointing outwards with magnitude equal to the area of the square. Then taking the dot product with the electric field effectively multiples the component of the electric field perpendicular to the surface by the area of the small piece. Taking the sum of all these products and taking the limit as the squares get very small gives us a surface integral, which is in some sense a measure of how much the electric field points out of the surface, as it ignores the component that is points along the surface.
One useful way to think about a surface integral is to imagine that the electric field is actually representing the flow of water, which the magnitude and direction of the electric field represent the speed and direction of water flowing through that point. In this case the electric flux through a surface is how much water flows out of the surface per unit time. A positive electric flux means water is flowing out, a negative electric flux means water is flowing in, and a electric flux of zero means that the total flow in equals the total flow out.
Continuing with the water flow analogy, we can consider the implication of Gauss's Law, which states that the electric flux through a closed surface is proportional to the enclosed charge. This is equivalent to saying (in out water analogy) that if there is a net flow of water out of a closed surface, then there must be some source (such as a faucet constantly pouring out water), and that if there is more outward flow then there must either be more faucets or they must be pouring out water faster. Similarly, if there is a net flow of water into a surface, then there must be a sink constantly sucking up water, and that if there is more inward flow then there must be more sinks or they must be sucking up water faster. In terms of the electric field positive charges play the role of faucets and negative charges play the role of sinks. If there is a positive electric flux through a closed surface, then there must be a net positive charge inside, and similarly a negative flux through a closed surface means there must be a net negative charge inside.
The fascinating property of Gauss's Law is that it does not depend on where inside the surface the charges are locate, or even how the surface is shaped. If two completely different closed surfaces contain the same net charge, the electric flux through them will be the same. If the charges are distributed in completely different configurations, so long as the total net charge is the same,they will have the same electric flux. We can use this property to easily calculate the electric field due to charge distributions in which is it easy to calculate the electric flux. We will see some examples.
Examples
Q: Derive Coulombs Law using Gauss's Law.
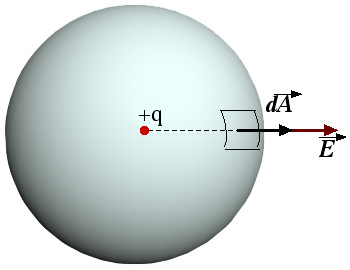
A: Suppose there is a point charge . Imagine a surface surrounding the point with radius . We must calculate the electric flux through this surface from from the point charge. First we note that the electric field on the surface of the sphere must always be perpendicular to the sphere. We can say this not because we secretly already know Coulomb's Law and thus know the electric field must point radially out from the point charge, but by appealing to symmetry. It is worth labouring a bit on the concept of symmetry because it is an important tool in physics: Suppose that the electric field at the surface were not perpendicular to the surface. Then it must be pointing in some particular direction, say slightly to the left. But then we could simply walk around to the other side of the sphere and it would look like the field was pointing slightly to the right. In both views however, the physical situation was identical since the point charge still is at the center of the sphere. If the charge were not in the center we could not make this argument, since when you moved to the other side, the electric field would change direction, but the charge would have flipped sides as well. It is a general principle of physics that the Laws of Physics should be true no matter what angle you look at the situation. Thus we can conclude that the above situation cannot be true if the charge is at the center and that the electric field must be perpendicular to the surface everywhere.
Once we've done that we can also conclude by symmetry that the electric field must have the same magnitude at every point. (Suppose this were not the case, and that the electric field was stronger on one side. Then if you looked at it from the other side, we would have the same geometric situation but the electric field would now be stronger on the right). With these assumptions, we can simplify Gauss's Law:
We can take the electric field out of the integral because we know that it only has a radial component and is the same magnitude everywhere on the surface. By using the formula for the surface area of a sphere and applying Gauss's Law, we can conclude:
Which is Coulomb's Law!
Q: Suppose there is an infinitely long straight wire carrying uniform charge per unit length (see diagram). What is the electric field of this charge distribution?
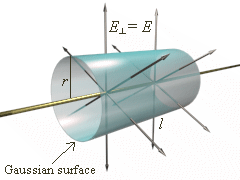
A: We can use Gauss's Law because this problem has so-called 'cylindrical' symmetry. Imagine a cylindrical surface along some finite length of the wire with the wire right on top of the cylinder axis. We can argue by symmetry that the electric field must be pointing directly away from the wire and perpendicular to the outer surface of the cylinder at all points. Try to imagine how, if this were not the case, you could look at the cylinder from a different angle or shift the cylinder along the wire to find a contradiction in direction of the field as we did above. Note that if the wire were not infinitely long, this would not and is not the case, since the field at the ends could be different than the field at the center. In practice, this result will hold as a good approximation of the field near the center of very long wires.
In order to apply Gauss's Law, we must close our surface. To do so we can simply add flat caps to the ends of the cylinder. If the caps are flat, then we know that they will not contribute to the electric flux since we determined that the electric field will always be pointing radially away from the wire and thus parallel to these caps (recall from the definition of surface integral that it ignores parallel components).
Now that we have a closed surface, we apply Gauss's Law:
Where we have used the formula for the surface area of a cylinder (ignoring the caps as we discussed) and the total charge enclosed is simply the length of the cylinder times the linear charge density. Now we solve for to find:
Thus this is the magnitude of the field at a distance from the wire, with the direction pointing radially away from the wire.
Q: Find the electric field of an infinite charged plate with uniform surface charge density .
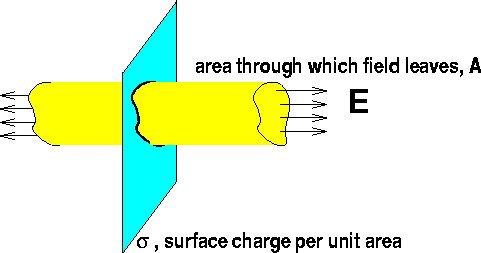
A: By symmetry, we know that the electric field will be perpendicular to the plate, and that it must be symmetric with respect to reflection about the plate (ie: the electric field should act the same above the plate as below the plate). We can imagine a cylindrical surface with two faces of the cylinder perpendiculat to the charged plate and at equal distances from it. Since the surface integral ignores parallel components of the electric field, we can ignore the contributions to the surface integral from the sides of the cylinder, since they are parallel to the electric field. Also, since the remaining faces of the box are at equal distance from the charged plate, the electric field must have the same magnitude on each face (by symmetry). Furthermore, the field at each face will either both point in or both point out of the box (depending on the sign of sigma), again by symmetry. Thus Gauss's Law becomes:
Where is the area of a face. Thus we solve for :

























