Course:PHYS350/Chaotic Motion

Definition

I think that it is important to define chaotic motion precisely, if we are to try to understand it. A system is said to exhibit chaotic motion if the deviation between two initially close paths in phase space increases exponentially with time generically.

Some Examples of Non-Chaotic Motion

Phase-space trajecories for a pendulum

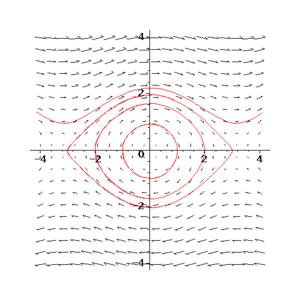
The phase-space diagram of a pendulum shows that for some initial conditions you can end up librating and some other neighboring initial conditions you can end up rotating. These seem to be vastly different.

Is the motion chaotic? No, because these are not generic initial conditions.

What about if I start two pendulums on different loops near the center? The outer loops take longer to traverse than the inner loops, so the two pendulums deviate from each other more and more as time passes.

Is the motion chaotic? No, because the deviation only increases linearly. A nice analogy to see this is two people running around a track at different speeds. There get more and more separate with time and if you didn't know how long they had been running it would be difficult to see that they started next to each other. However, they is nothing really chaotic about the whole thing.

Some Mathematics

In chaotic motion, the difference between to systems increases exponentially in time in at least one coordinate. Let's continue to look at one-dimensional motion. Here we have it $\Delta q=\Delta q_{0}e^{\lambda t}.\left.\right.$ This means that $\Delta {\dot {q}}=\lambda \Delta q\left.\right.$ Let's use the definition of the conjugate momentum to look at this further. We have

$\Delta p={\frac {\partial ^{2}L}{\partial {\dot {q}}^{2}}}\Delta {\dot {q}}+{\frac {\partial ^{2}L}{\partial q\partial {\dot {q}}}}\Delta q=\left(\lambda {\frac {\partial ^{2}L}{\partial {\dot {q}}^{2}}}+{\frac {\partial ^{2}L}{\partial q\partial {\dot {q}}}}\right)\Delta q,$

so we find that the deviation to the momentum conjugate to the coordinate also increases exponentially.

Let's write down the volume in phase space occupied by our systems, still for one-dimensional motion

$\Delta q\Delta p=\Delta q_{0}\Delta p_{0}e^{2\lambda t}\left.\right.$

and calculate the phase-space density

$f={\frac {N}{\Delta q\Delta p}}={\frac {N}{\Delta q_{0}\Delta p_{0}}}e^{-2\lambda t}.$

Because the phase space density must be constant, we find that $\lambda =0$ and we cannot have chaotic motion in one-dimension. This is not too surprising when one recalls that one-dimensional conservative systems can be integrated at least formally no matter what.

In more than one-dimension we find that

$\sum _{i}\lambda _{i}+\sum _{i}\lambda _{p,i}=0\left.\right.$

so the deviation must decrease in some coordinates or momenta while it increases in others.

A Chaotic System - The Double Pendulum

We need at least two degrees of freedom to have a chaotic system. We have integrated several systems with two or more degrees of freedom: planetary orbits, two-dimensional harmonic oscillators, coupled oscillators. Because we solved them they probably don't exhibit chaotic motion. How about the double pendulum?

The Double Pendulum

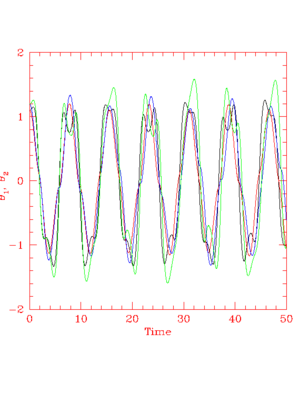
We need at least two degrees of freedom to have a chaotic system. We have integrated several systems with two or more degrees of freedom: planetary orbits, two-dimensional harmonic oscillators, coupled oscillators. Because we solved them they probably don't exhibit chaotic motion. How about the double pendulum?

It turns out that the simple double pendulum is pathological, so we will have to be a bit more sophisticated in our modelling of this system. Specifically, let's imagine we have two thin rods ($I={\frac {1}{12}}Ml^{2}$) connected by a pivot and the end of one rod suspended from a pivot.

It is natural to define the coordinates to be the angle between each rod and the vertical. We will denote this by θ₁ and θ₂. We can write the position of the centre of mass of the two rods in terms of these coordinates. We have

$x_{1}={\frac {l}{2}}\sin \theta _{1},$ $x_{2}=l\left(\sin \theta _{1}+{\frac {1}{2}}\sin \theta _{2}\right),$ $y_{1}=-{\frac {l}{2}}\cos \theta _{1}$ and $y_{2}=-l\left(\cos \theta _{1}+{\frac {1}{2}}\cos \theta _{2}\right).$

This is enough information to write out the Lagrangian.

Lagrangian

The Lagrangian is given by $L={\frac {1}{2}}m\left(v_{1}^{2}+v_{2}^{2}\right)+{\frac {1}{2}}I\left({{\dot {\theta }}_{1}}^{2}+{{\dot {\theta }}_{1}}^{2}\right)-mg\left(y_{1}+y_{2}\right)$ where we have taken the kinetic energy to be sum of the kinetic energy of the centre of mass of each rod and the kinetic energy about the centres of mass of the rods. The potential energy of a body in a uniform gravitational field is given by the potential energy at the centre of mass.

Plugging in the coordinates above and doing a bit of algebra gives $L={\frac {1}{6}}ml^{2}\left[{{\dot {\theta }}_{2}}^{2}+4{{\dot {\theta }}_{1}}^{2}+3{{\dot {\theta }}_{1}}{{\dot {\theta }}_{2}}\cos(\theta _{1}-\theta _{2})\right]+{\frac {1}{2}}mgl\left(3\cos \theta _{1}+\cos \theta _{2}\right)$

Before we get the equations of motion, we find that there is only one conserved quantity (the energy), and no conserved momenta. We can write the two momenta as

$p_{\theta _{1}}={\frac {\partial L}{\partial {{\dot {\theta }}_{1}}}}={\frac {1}{6}}ml^{2}\left[8{{\dot {\theta }}_{1}}+3{{\dot {\theta }}_{2}}\cos(\theta _{1}-\theta _{2})\right]$ and $p_{\theta _{2}}={\frac {\partial L}{\partial {{\dot {\theta }}_{2}}}}={\frac {1}{6}}ml^{2}\left[2{{\dot {\theta }}_{2}}+3{{\dot {\theta }}_{1}}\cos(\theta _{1}-\theta _{2})\right]$

Let's invert these expressions to get

${{\dot {\theta }}_{1}}={\frac {6}{ml^{2}}}{\frac {2p_{\theta _{1}}-3\cos(\theta _{1}-\theta _{2})p_{\theta _{2}}}{16-9\cos ^{2}(\theta _{1}-\theta _{2})}}$ and ${{\dot {\theta }}_{2}}={\frac {6}{ml^{2}}}{\frac {8p_{\theta _{2}}-3\cos(\theta _{1}-\theta _{2})p_{\theta _{1}}}{16-9\cos ^{2}(\theta _{1}-\theta _{2})}}$

We can write the remaining equations of motion as

${{\dot {p}}_{\theta _{1}}}={\frac {\partial L}{\partial \theta _{1}}}=-{\frac {1}{2}}ml^{2}\left[{{\dot {\theta }}_{1}}{{\dot {\theta }}_{2}}\sin(\theta _{1}-\theta _{2})+3{\frac {g}{l}}\sin \theta _{1}\right]$

and

${{\dot {p}}_{\theta _{2}}}={\frac {\partial L}{\partial \theta _{2}}}=-{\frac {1}{2}}ml^{2}\left[-{{\dot {\theta }}_{1}}{{\dot {\theta }}_{2}}\sin(\theta _{1}-\theta _{2})+{\frac {g}{l}}\sin \theta _{2}\right]$

Poincaré Plot

Often one has to look at a system for a really long time before its chaotic nature becomes evident. Furthermore, phase space has a lot of dimensions to it so it is quite hard to visualize what is happen. Henri Poincaré devised a neat way to study trajectories through phase space. Define a region in phase space and plot where the trajectory intersects the region, and finally project the region onto a plane.

In the case of the pendulum we are going to look at the plane $(\theta _{1},p_{\theta _{1}})$ for $\sin \theta _{2}=0$. To illustrate the onset of chaos, we start will slightly different initial conditions and plot the Poincaré plots for about one thousand oscillations of the system.

Fractals

Chaotic motion is intimately connected with fractals. For example, we could plot whether either pendulum flips within a set period of time as a function of the initial conditions to see the general structure of the solutions.

Does either pendulum flip as a function of the initial conditions?

Zoom-in on the swirly region on the upper left

We have plotted along the x-direction, the value of θ₁ from -3 to 3 and along the y-direction the value of θ₂ from -3 to 3. The colour of each pixel indicates whether either pendulum flips within 10 ${\sqrt {g/l}}$ (green), within 100 (red), 1000 (purple) or 10000 (blue). Those that don't flip within 10000 ${\sqrt {g/l}}$ are plotted white.

The boundary of the central white region is defined in part by energy conservation (see this solution for further details) with the following curve $3\cos \theta _{1}+\cos \theta _{2}=2\,$ Within the region defined by this curve, that is if $3\cos \theta _{1}+\cos \theta _{2}>2\,$ it is energetically impossible for either pendulum to flip. Outside this region, the pendulums can flip but this is different from determining when they will flip.

Poincaré Recurrence Theorem

A system that visits essentially all of the phase space available to it energetically is called ergodic. Most multidimensional systems are ergodic and most ergodic systems are chaotic in the sense that they are not integrable. However, some integrable systems are ergodic. For example if a system exhibits more than one oscillation frequency and these frequencies are not comeasureable (there are no integers $a$ and $b$ such that $a\omega _{1}=b\omega _{2}$), then the system will visit all of the phase space available to it.

A surprising concept related to this is the fact that a finite system that follows Hamilton's equations will eventually return arbitrarily close to its initial conditions. Let's take a small volume in phase space in a neighborhood of the initial conditions and follow its path with Hamilton's equations through phase space. The size of the volume cannot contract or expand due to Lioville's theorem and the trajectories cannot intersect each other without repeating; therefore, the volume sweeps out new regions of phase space until it either comes within a small neighborhood of where it started and it repeats or it has filled the entire phase space save a few points of measure zero by which time it must have come within a small neighborhood of where it started.

An everyday example of this is that if you are painting a wall (even a really big one) with a brush (even a really small one) and you cannot intersect your path, then you will eventually come within a small neighborhood of where you started.

We can prove this in a more rigorous way. Let's denote the initial neighborhood around the initial conditions as $D_{0}$ and denote $D_{k}$ as the evolution of this region through phase space under the Hamiltonian over a time $kT$. From Liouville's theorem we know that the volume of the neighborhood is constant

${\rm {Vol}}\left(D_{0}\right)={\rm {Vol}}\left(D_{1}\right)={\rm {Vol}}\left(D_{k}\right).$

Let's calculate the volume of the union of all of these sets

${\rm {Vol}}\left[\cup _{k=0}^{\infty }D_{k}\right]=\lim _{k\rightarrow \infty }k{\rm {Vol}}\left(D_{0}\right)-{\rm {Vol}}\left[\cap _{k=0}^{\infty }D_{k}\right].$

Because the total volume of phase space is finite, the sets $D_{k}$ and $D_{k'}$ must intersect for at least some values of $k$ and $k'$. Let's take $k'>k$ and define

$\omega _{k,k'}=D_{k}\cap D_{k'}\neq \phi .$

We can invert the Hamiltonian mapping so we have

$\omega _{0,k'-k}=D_{0}\cup D_{k'-k}\neq \phi$

so some point $P'\in D_{0}$ has returned to $D_{0}$ in $k'-k$ time steps $T$.

How long to recur?

This theorem leads to some apparent paradoxes. For example, let's say that you have a box with a partition down the middle. There is gas on one side of the box and you pull the partition out so that the gas flows to the other side. The recurrence theorem says that if you wait long enough you will find all of the gas on one side of the box again. This seems to violate the second law of thermodynamics that insists that entropy increases or remains the same. Indeed it does, but the second law is a statistical statement; entropy almost never decreases.

Let's estimate what is the maximum time for this to occur. We need to estimate the rate that the phase tube fills phase space and what fraction of phase space has all of the particles on the same side of the box. The total volume of the phase space is the volume of the box raised to the power of the number of particles in the box times the volume of momentum space,

$V_{\rm {total}}=V^{n}\left(\Delta p\right)^{n}$

Seeing all of the particles on the same side of the box restricts the physical volume that they occupy but not their momentum, so we have

$V_{\rm {half}}=\left({\frac {V}{2}}\right)^{n}\left(\Delta p\right)^{n}$

and the fraction is given by

$f={\frac {V_{\rm {half}}}{V_{\rm {total}}}}=2^{-n}$

so the maximum recurrance time is

$t_{\rm {recur}}=2^{n}\Delta t$

where $\Delta t$ is the typical time for the phase trajectory to move to a new part of phase space, the time for a particle to travel the width of the box (a fraction of a second perhaps). Let's estimate the prefactor, assuming that the box is a meter on a side and the density of the gas is about 1.25 kg m^-3. The number of molecules in the box is about

$n=1.25\times {\frac {6.022\times 10^{26}}{14}}=5\times 10^{25}$

so we have

$t_{\rm {recur}}=2^{5\times 10^{25}}\Delta t=10^{1.5\times 10^{25}}\Delta t$

which is clearly a long time regardless of what $\Delta t$ is. The current age of the universe is about $4\times 10^{17}$ seconds.