Course:PHYS350/Simple Double Pendulum

The Simple Double Pendulum

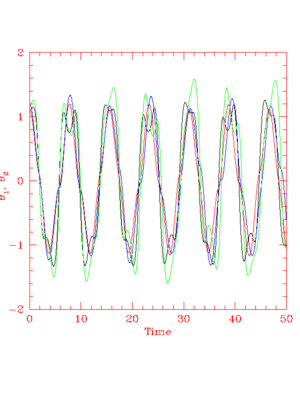
We need at least two degrees of freedom to have a chaotic system. We have integrated several systems with two or more degrees of freedom: planetary orbits, two-dimensional harmonic oscillators, coupled oscillators. Because we solved them they probably don't exhibit chaotic motion. How about the double pendulum?

It is natural to define the coordinates to be the angle between each string and the vertical. We will denote this by θ₁ and θ₂. We can write the position of the bob in terms of these coordinates. We have

$x=l(\sin {\theta }_1+\sin {\theta }_2)$

and

$y=-l(\cos {\theta }_1+\cos {\theta }_2).$

This is enough information to write out the Lagrangian.

Lagrangian

$L=\frac{1}{2}m{v}^2-mgy=\frac{1}{2}m{l}^2(2{\dot{\theta }}_1{\dot{\theta }}_2\cos ({\theta }_1-{\theta }_2)+{{\dot{\theta }}_1}^2+{{\dot{\theta }}_2}^2)+mgl(\cos {\theta }_1+\cos {\theta }_2)$

Let's divide both sides by $m{l}^2$. This will not change the equations of motion. $L=\frac{1}{2}(2{\dot{\theta }}_1{\dot{\theta }}_2\cos ({\theta }_1-{\theta }_2)+{{\dot{\theta }}_1}^2+{{\dot{\theta }}_2}^2)+\frac{g}{l}(\cos {\theta }_1+\cos {\theta }_2)$

Before we get the equations of motion, we find that there is only one conserved quantity (the energy), and no conserved momenta. We can write the two momenta as

$p_{{\theta }_1}=\frac{\partial L}{\partial {\dot{\theta }}_1}={\dot{\theta }}_2\cos ({\theta }_1-{\theta }_2)+{\dot{\theta }}_1$ and $p_{{\theta }_2}=\frac{\partial L}{\partial {\dot{\theta }}_2}={\dot{\theta }}_1\cos ({\theta }_1-{\theta }_2)+{\dot{\theta }}_2$

Let's invert these expressions to get

${\dot{\theta }}_1=\frac{p_{{\theta }_1}-\cos ({\theta }_1-{\theta }_2)p_{{\theta }_2}}{{\sin }^2({\theta }_1-{\theta }_2)}$ and ${\dot{\theta }}_2=\frac{p_{{\theta }_2}-\cos ({\theta }_1-{\theta }_2)p_{{\theta }_1}}{{\sin }^2({\theta }_1-{\theta }_2)}$

and we can write the Hamiltonian

$H=T+V=\frac{p_{{\theta }_1}^2+p_{{\theta }_2}^2-2\cos ({\theta }_1-{\theta }_2)p_{{\theta }_1}{p}_{{\theta }_2}}{2{\sin }^2({\theta }_1-{\theta }_2)}+\frac{g}{l}(\cos {\theta }_1+\cos {\theta }_2)$

and get Hamilton's equations

${\dot{p}}_{{\theta }_1}=-\frac{\partial H}{\partial {\theta }_1}=-\frac{p_{{\theta }_1}{p}_{{\theta }_2}}{\sin ({\theta }_1-{\theta }_2)}+\frac{p_{{\theta }_1}^2+p_{{\theta }_2}^2+2\cos ({\theta }_1-{\theta }_2)p_{{\theta }_1}{p}_{{\theta }_2}}{{\sin }^3({\theta }_1-{\theta }_2)}-{\omega }^2\sin {\theta }_1,$

${\dot{p}}_{{\theta }_2}=-\frac{\partial H}{\partial {\theta }_2}=+\frac{p_{{\theta }_1}{p}_{{\theta }_2}}{\sin ({\theta }_1-{\theta }_2)}-\frac{p_{{\theta }_1}^2+p_{{\theta }_2}^2+2\cos ({\theta }_1-{\theta }_2)p_{{\theta }_1}{p}_{{\theta }_2}}{{\sin }^3({\theta }_1-{\theta }_2)}-{\omega }^2\sin {\theta }_2,$

${\dot{\theta }}_1=\frac{\partial H}{\partial p_{{\theta }_1}}=\frac{2p_{{\theta }_1}-2\cos ({\theta }_1-{\theta }_2)p_{{\theta }_2}}{{\sin }^2({\theta }_1-{\theta }_2)}$

${\dot{\theta }}_2=\frac{\partial H}{\partial p_{{\theta }_2}}=\frac{2p_{{\theta }_2}-2\cos ({\theta }_1-{\theta }_2)p_{{\theta }_1}}{{\sin }^2({\theta }_1-{\theta }_2)}$

Another Coordinate System

Things look a bit simpler in a new set of coordinates. Let's take $\delta =\frac{{\theta }_1-{\theta }_2}{2}$ and $\sigma =\frac{{\theta }_1+{\theta }_2}{2}$, so we have ${\theta }_1=\sigma +\delta$ and ${\theta }_2=\sigma -\delta$. Let's write out the Lagrangian

$L=2{\dot{\sigma }}^2{\cos }^2\delta +2{\dot{\delta }}^2{\sin }^2\delta +2\frac{g}{l}\cos \sigma \cos \delta$

and get the momenta $p_{\sigma }=4\dot{\sigma }{\cos }^2\delta$ and $p_{\delta }=4\dot{\delta }{\sin }^2\delta$ and the Hamiltonian

$H=\frac{p_{\sigma }^2}{8{\cos }^2\delta }+\frac{p_{\delta }^2}{8{\sin }^2\delta }-2\frac{g}{l}\cos \sigma \cos \delta .$

Hamilton's equations are a bit simpler here but still singular

${\dot{p}}_{\sigma }=-\frac{\partial H}{\partial \sigma }=-2\frac{g}{l}\sin \sigma \cos \delta$

${\dot{p}}_{\delta }=-\frac{\partial H}{\partial \delta }=-\frac{p_{\sigma }^2}{4{\cos }^3\delta }\sin \delta +\frac{p_{\delta }^2}{4{\sin }^3\delta }\cos \delta -2\frac{g}{l}\cos \sigma \sin \delta$

$\dot{\sigma }=\frac{\partial H}{\partial p_{\sigma }}=\frac{p_{\sigma }}{4{\cos }^2\delta }$

$\dot{\delta }=\frac{\partial H}{\partial p_{\delta }}=\frac{p_{\delta }}{4{\sin }^2\delta }$

We see that things go wacky when ${\cos }^2\delta =0$ or ${\sin }^2\delta =0$ which corresponds to ${\theta }_1-{\theta }_2=0,\pi ,2\pi$ etc.