Course:PHYS341/Archive/2016wTerm2/HowtheSympatheticStringsoftheSarangiHelpMimictheHumanVoice

The sarangi is a chambered string instrument from India and Nepal. Its three main strings are played with a bow. In addition to the playing strings, between 30 to 35 additional auxiliary strings pass through the instrument’s main bridge. These are typically not played but are present to vibrate sympathetically to give the instrument its distinctive human voice-like sound.

Structure of the Sarangi

Typical sarangi

The sarangi is a multi-string (up to 36) musical instrument made up of three parts: the head, neck and belly. Strings run from the belly, along the neck, to the head. The body of the instrument itself is composed of an Indian cedar called tun, and its soundboard is covered by goatskin. There are three playing strings. Of the remaining strings, tarafs, 24 (consisting of a set of nine and another of fifteen) run up the neck to pegs located on one side of the instrument, and the remaining nine are attached in two groups at the top of the neck and pass over small bridges called jawari. All strings on the instrument pass through the main bridge.

The fifteen side tarafs are usually tuned to the chromatic scale, the other nine according to the rag, while the strings running over the jawari are more arbitrarily tuned.

Physics of Resonance

In acoustics, resonance is when a vibrating system such as a string drives another system to vibrate at frequencies that matches one of its own natural frequencies. Strings in specific, naturally vibrate at more than one resonant frequency. The classic example of this transfer of energy is shown by the tuning fork experiment. When a passive string starts to vibrate in response to the external oscillating force, we call this sympathetic resonance or vibration.

Sympathetic Resonance Experiments

Classical Western Instruments

The bulk of the available literature on sympathetic strings is for western instruments. One will find usefulness in examining those findings as they apply to the sarangi.

Piano

Single, and double and triple unison groups of strings and their corresponding keys

In an experiment exploring the coupled oscillation of piano strings using a capacitive motion probe, marked differences in vibration were found depending on which strings of a unison group of strings were allowed to sound. The strings at the treble end of a grand piano are weaker than the thicker bass strings, so higher notes employ two or three identically tuned, or unison, strings. Weinreich found that when only one string was struck by the hammer and the other two were prevented from vibrating by means of felt wedges, the decay time for the struck string was on the order of five seconds. A plot of vibration level for that string versus time showed a single spike reaching 0 dB before dropping to -50 dB. However, when one felt wedge was removed so that one other string could vibrate freely, the decay time was on the order of 30 s for the struck string. The pattern consisted of a short sharp rise to 0 dB, followed by a quick drop to -20 dB, and then a small rise to -10 dB, before the gradual, linear, 30 s decrease in amplitude occurs, showing that the original string vibrates for a much longer time. The original string's vibration had been energized by the other. The sound is perceived as being more loud and sustained.

Violin

M. Demoucron and S. Weisser examined the effect of sympathetic resonance (vibrations) on the main string and overall sound of a violin, with the ultimate aim to see how this compares with a sarangi. They do make a distinction between the sympathetic vibrations of a violin and those of a sarangi. The former they consider as “coupled strings” owing to the fact that the phenomenon is collateral in nature, occurring between adjacent played strings, whereas in the latter, the vibrations happen in the non-played “sympathetic strings”. In other words, the played strings are left to vibrate as a side effect rather than by design.

Sound measurements with a microphone were made for ten situations when tones were played on the G string. The strings were either all damped, each individually undamped (just string D, then A, then E), or all were free to vibrate. This was done for two types of bow strokes: solid staccato, where the main string is quickly damped and the coupled strings are left to vibrate, and flying staccato, where the main string is left to vibrate freely.

Using Fast Fourier Transform, plots of the first six partials were created, showing the relationship between power (dB) and time. The results for the solid staccato obeyed theory: the freely-vibrating strings with harmonics that are multiples of the first harmonic of the played tone resonated accordingly. The flying staccato situation was more interesting. Their paper showed graphs of time versus power for four cases (strings all damped, all but D, all but A, none damped). Compared to the solid staccato, the total power decayed much more slowly because of modulations from the presence of sympathetic strings. The authors believe this phenomena adds to the "floating" characteristic of the overall sound.

Sarangi

Summary of Demoucron's sarangi experiment

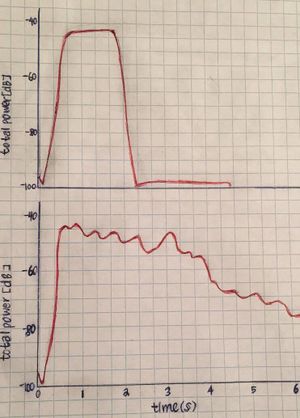
M. Demoucron and S. Weisser then went on to examine the effect of playing the sarangi with tarafs, and with the tarafs damped by cloth so that they could not vibrate. They recorded the notes using microphones. The results were analyzed by extracting the first twenty harmonics and establishing the relationship of amplitude as a function of time. A note is played with the bow and the bow is suddenly stopped. For the case of the damped tarafs, the plot of the harmonics and the total amplitude start off at -100 dB, quickly rise and stay horizontal until the bow stops at time 2.2 s after which there was a steep drop back to -100 dB. However, with the tarafs, the graph of the harmonics start off the same for a fraction of a second, but then decrease slowly in a roughly linear fashion thereafter, with appreciable amplitude even after 6 s. The authors attribute this latter behaviour to modulations between the harmonics of the tarafs.

Comparison of Human Voice to Sarangi

Ranade compared the frequency of various Indian instruments with the male and female human voice. The sarangi has most of its frequencies between 200 and 4,000 cycles, peaking at around 315. The male voice is concentrated between 100 and 1,800, peaking at 315, while the female is between 150 and 2,500, peaking at 400 cycles. Other instruments had peaks at 1,600 or 100, quite different from the sarangi and human voice.

Summary

The sarangi has a unique sound because of the

1. Large number of sympathetic strings that result in modulations between their harmonics, further resulting in a slow decay time and sustained quality.
2. Frequency spectra that mimics that of the human voice.
3. Wide possibilities of string tunings.

Bibliography

• White, Harvey; White, Donald (1980). [www.doverpublications.com Physics and Music The Science of Musical Sound]. Mineola, New York: Dover Pulications, Inc. ISBN 978-0-486-77934-8.

• "The Sarangi". www.chembur.com. 1999–2003.CS1 maint: date format (link)

• Courtney, David. "Parts of a Sarangi".

• Courtney, David. "SARANGI: AN OVERVIEW".