Course:MATH102/Question Challenge/2010 December Q7

	Questions? Click here to add or read comments for this problem
Please rate how easy you found this problem: {{#w4grb_rate:}} Hard                                              Easy

Question

A sector of a circle with radius $r$ and opening angle $\theta$ has area $A=r^{2}\theta /2$. Find $r$ and $\theta$ for the sector with the smallest perimeter, given that the area $A=9$. Note that the perimeter consists of two radii and a circular arc. Be sure to verify that your answer is the global minimum.

A sector of a circle of radius $r$

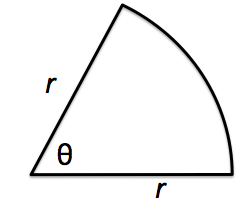
Hints

Hint 1
What is the length of the part of circle perimeter subtended by the angle $\theta$?. Note that if $\theta =2\pi$ then we have the entire circular perimeter, which is $2\pi r$

Hint 2
Use the fact that the area is constant to eliminate one of the variables from the equation for the perimeter.

Solutions

Solution

We are told that the area of the shape is constant and that: $A={\frac {r^{2}\theta }{2}}=9$. This will be a constraint in this optimization problem The perimeter of the shape is the sum of the circular arc and the two radii, so is : $P=r\theta +2r$. We want to minimize $P$. We first manipulate the constraint to isolate $\theta$ ${\frac {r^{2}\theta }{2}}=9$ $r^{2}\theta =18$ $\theta ={\frac {18}{r^{2}}}$ The next step is to substitute in this value of $\theta$ into the equation for the perimeter: $P(r)=r\left({\frac {18}{r^{2}}}\right)+2r$, $P(r)={\frac {18r}{r^{2}}}+2r$, $P(r)={\frac {18}{r}}+2r$. This is a function of a single variable, $r$, so now, to find a critical point, set $P'(r)=0$ and solve for the radius: $P'(r)={\frac {-18}{r^{2}}}+2=0$ ${\frac {18}{r^{2}}}=2$ $2r^{2}=18$ $r^{2}=9$ $r=\pm 3$. Rejecting the negative root, we substitute $r=3$ into the equation for $\theta$: $\theta ={\frac {18}{r^{2}}}={\frac {18}{3^{2}}}=2$ radians To check that these values of $r$ and $\theta$ produce a sector with minimal perimeter for a fixed area of 9, we determine the sign of the second derivative $P''(r)={\frac {36}{r^{3}}}$. For any positive value of $r$, we see that $P''(r)>0$, so the critical point is a local minimum. (It is optional to actually plug in $r=3$ and find that $P''={\frac {36}{(3)^{3}}}={\frac {36}{27}}$. The exact value does not matter, as we already know that it is positive.) We conclude that the values we have found, namely $r=3$ units, $\theta =2$ radians produce a sector of minimal perimeter.