Course:MATH102/Question Challenge/2008 December Q9

	Questions? Click here to add or read comments for this problem
Please rate how easy you found this problem: {{#w4grb_rate:}} Hard                                              Easy

Question

Graduate student Ryan Lukeman studied the behaviour of duck flocks swimming near Canada Place in Vancouver, BC. This figure from his PhD thesis shows his photography set-up. Here $H=10$ meters is the height from sea level up to his camera aperture at the observation point,$D=2$ meters is the width of a pier (a stationary platform whose size is fixed), and $x$ is the distance from the pier to the leading duck in the flock (in meters). $\alpha$ is a visual angle subtended at the camera, as shown.

An observer at height H photographing ducks.

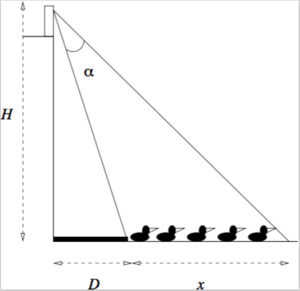
If the visual angle is increasing at the rate of 1/100 radians per second, at what rate is the distance $x$ changing at the instant that $x=3$ meters?

${\displaystyle }$

Hints

Hint 1
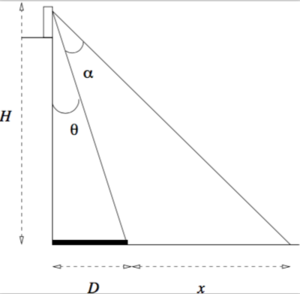Consider the angles $\theta +\alpha$ and $\alpha$ and write down trigonometric functions relating these angles to the distances in the diagram.

Solutions

Solution

Consider the angles in the diagram, and note the definition of the angle $\theta$. Consider the angles $\theta +\alpha$ and $\alpha$ and write down trigonometric functions relating these angles to the distances in the diagram. Then $\tan \theta =\frac{D}{H}=\frac{2}{10}=\frac{1}{5}$. $\tan (\theta +\alpha )=\frac{D+x}{10}=\frac{2+x}{10}$. $\arctan \left(\frac{2+x}{10}\right)=\theta +\alpha$ $\alpha =\arctan \left(\frac{2+x}{10}\right)-\theta$ We are told that the visual angle $\alpha$ is increasing at the date of 1/100 radians per sec. This means that $\frac{d\alpha }{dt}=\frac{1}{100}$ Taking the first derivative: $\frac{d\alpha }{dt}=\frac{1}{1+((2+x)/10{)}^2}\cdot \frac{1}{10}\cdot \frac{dx}{dt}$ $\frac{1}{100}=\frac{1}{1+1/4}\cdot \frac{1}{10}\cdot \frac{dx}{dt}$ $\frac{1}{100}=\frac{4}{5}\cdot \frac{1}{10}\cdot \frac{dx}{dt}$ $\frac{dx}{dt}=\frac{50}{400}=\frac{1}{8}=0.125$ meters per second. If the visual angle is increasing at $1/100$ radians per second, then at the instant $x=3$meters, $\frac{dx}{dt}=1/8=0.125$ meters per second.