Course:MATH102/Question Challenge/2001 December Q9

	Questions? Click here to add or read comments for this problem
Please rate how easy you found this problem: {{#w4grb_rate:}} Hard                                              Easy

Question

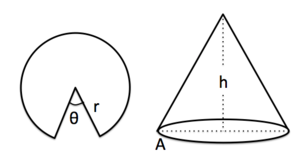
A wedge-shaped region is cut out of a circle of fixed radius $r$ and the cut edges are joined to produce a cone, as shown in the figure. The remaining part of the circle's perimeter, whose length is $(2\pi -\theta )r$ forms the bottom edge of the cone. For what angle $\theta$ is the volume of the resulting cone greatest?

Recall that the volume of a cone is $V={\frac {1}{3}}\pi R^{2}h$ where $R$ is the radius of the base of the cone.

The edges of the flat shape at left are joined to form a cone of greatest volume.

Hints

Hint 1
You are given the length of the perimeter of the cone's base. Use that information to write down the radius $R$ of that base.

Hint 2
A slice through the axis of the cone is a triangle. Relate the height $h$ and base radius $R$ of the cone to the radius $r$ of the original circle.

Solutions

Solution

$r=$ radius of the circle = constant θ = the angle formed by cutting out a section of the circle; we must optimize this to produce the largest possible volume for the cone For the Pythagorean triangle seen in the cross section of the cone: $r^{2}=R^{2}+h^{2}$, where $r$ is the radius of the circle, $R$ is the radius of the base of the cone, and $h$ is the height of the cone. This relationship is a constraint. $R$ and $h$ are variables dependent on θ. The volume of the cone is given by: $V=(1/3)\pi (R^{2})h$ Rearrange the constraint to: $R^{2}=r^{2}-h^{2}$ We can substitute this into the equation for volume to obtain: $V(h)=(1/3)\pi (r^{2}-h^{2})h$. (Note that since $r$ is constant, $V$ is now a function of just one variable, $h$.) This simplifies to: $V(h)=(1/3)\pi (r^{2})h-(1/3)\pi (h^{3})$ We obtain the derivative of this function and equate it to zero to maximize the volume: $V'(h)=(1/3)\pi (r^{2})-\pi (h^{2})$ $(1/3)\pi (r^{2})=\pi (h^{2})$ $(r^{2})/3=h^{2}$ To check that this is in fact a maximum we take the second derivative and substitute in our or critical point for $h$: $V''(h)=-2\pi h$ $V''(h)=-2\pi (r/({\sqrt {3}}))$ Since $h$ is a positive value, the second derivative must be negative for this value of h. This proves that we have found a maximum. Now we want to find the cone's base radius, $R$. Substituting in for $h^{2}$ into the equation for the cross-section of the cone we find: $R^{2}=r^{2}-(1/3)(r^{2})$ $R^{2}=(2/3)(r^{2})$ $R=({\sqrt {2/3}})r$ We are told that: $(2\pi -\theta )r=$ the circumference of the base of the cone Therefore: $(2\pi -\theta )r=(2\pi )R$ Substituting in the R we know gives the cone of maximum volume we find: $(2\pi -\theta )r=2\pi ({\sqrt {2/3}})r$ $2\pi -\theta =2\pi ({\sqrt {2/3}})$ $\theta =2\pi -2\pi ({\sqrt {2/3}})$ $\theta =2\pi (1-({\sqrt {2/3}}))$ θ = 1.15 rad = 66.06 degrees