Course:MATH102/Question Challenge/1998 December Q3

	Questions? Click here to add or read comments for this problem
Please rate how easy you found this problem: {{#w4grb_rate:}} Hard                                              Easy

Question

Find the area of the largest rectangle that can be inscribed in the semi-circle of radius $a>0$.

A rectangle inscribed in a semicircle of radius $a$.

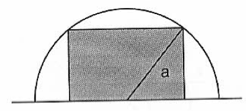
Hints

Hint 1
Use the coordinates $(x,y)$ to label the point on the circle at the corner of the rectangle. What is the relationship between $x$, $y$, and $a$? This relationship will be a constraint in this optimization problem.

Hint 2
What is the width and height of the rectangle in terms of $x$ and $y$?

Hint 3
Write down the area of the rectangle in terms of $x$ and $y$, then use the constraint to eliminate either $x$ or $y$.

Solutions

Solution

Let us try to solve the problem geometrically. The radius of the semi-circle forms two right triangles within the rectangle, one on the rectangle's left and one on its right. Due to symmetry, there are also another two congruent triangles mirrored along hypotenuse of both right triangles. Together these four right triangles make up the total area of the rectangle inscribed within the semi-circle. When we rearrange these right triangles we see they form a square with side-length $a$. The equation for the area of the square and therefore the area of the rectangle inscribed by the semi-circle is therefore: $A=a^{2}$