Course:CPSC532:StaRAI2020:R-GCN Attribute Aggregation

Title

R-GCN Attribute Aggregation & MLP Classification Using Dirichlet Priors

Authors: Obada Alhumsi

Abstract

This page evaluates three hypotheses for entity classification in knowledge graphs. Firstly, we hypothesize that the use of different aggregation functions in the relational graph convolutional network (R-GCN) architecture can yield better entity classification results. Secondly, we hypothesize that each aggregation function provides a node representation that has some unique value in determining the label of the node. Lastly, we hypothesize that by using prior probabilities as inputs to an MLP classifier, we can produce better classification results than R-GCNs.

Related Pages

This page first and second hypothesis manipulates the aggregation function in R-GCNs. The third hypothesis models priors using a Dirichlet distribution, a multivariant generalization of the beta distribution.

Content

Introduction

*Please note that this page uses the same definitions as in R-GCN*

There are many methods that are being used for entity classification in knowledge graphs; the most prominent method in the deep learning literature is the R-GCN, which provides state of the art results on multiple knowledge graph datasets. The R-GCN extends the graph convolutional network (GCN) by also considering the relation of the edges connecting the nodes. Nonetheless, the R-GCN inherits the same aggregation of neighboring nodes features used in GCN's. The aggregation function serves the goal of keeping the node representation size constant, regardless of the number of neighboring nodes features used in the aggregation. It also aims to distill the properties of the neighboring node features into one node representation vector. The R-GCN paper aggregates the node features by summing them up, however, this can be problematic as nodes with more edges will have a bigger sum than nodes with fewer edges. This page explores other methods of aggregation in the R-GCN network as well as proposes an alternative method of entity classification using Dirichlet priors and a MLP.

Hypothesees

We first start with a simple hypothesis; the use of other aggregation functions such as those used in the graph neural networks literature can provide better results in R-GCNs than aggregation by sum. Specifically, we hypothesize that aggregation by mean would provide better results, as it is not affected by the number of edges each node has. Nonetheless, we test other aggregations such as the minimum and maximum of node features and tabulate their results on entity classification.

Secondly, we hypothesize that each aggregation function provides a node representation that has some unique value in determining the label of the node. While some node representations offer more value than others, we believe that composing a new node representation based on the node representation computed by each aggregation function would provide superior results to using just one aggregation function. In our approach, we chose to compose the new node representation by passing the node representations of all aggregation functions into an MLP.

Lastly, we explore a different approach for entity classification in knowledge graphs where we learn a prior from the data available. To do so, we form a Dirichlet distribution for each node, each relation, and each node-relation pair parametrized by a vector $a$ = $[a_{1}+1,a_{2}+1,...,a_{k}+1]$ where $a_{k}$ is the number of times the node(as a source node), relation or the node-relation pair led to a destination node of class $k$. For each source node, we can then sample $[[P(class_{1}|node_{n}),P(class_{1}|relation_{r}),P(class_{1}|node_{n}\land relation_{r})],...[P(class_{k}|node_{n}),P(class_{k}|relation_{r}),P(class_{k}|node_{n}\land relation_{r})]]$ from the corrosponding Dirichlet distributions. We hypothesize that by feeding these sampled probabilities into an MLP, we can accuratly classify the class of the destination node.

RGCN Alterations Approachs

The approach for hypothesis 1 is self-explanatory, we simply aggregate the node features of neighboring nodes using different aggregation functions. In minimum and maximum aggregation, the node representation is equal to the minimum neighboring nodes feature and maximum neighboring nodes feature respectively. In mean aggregation, the node representation is equal to the mean of all neighboring nodes features.

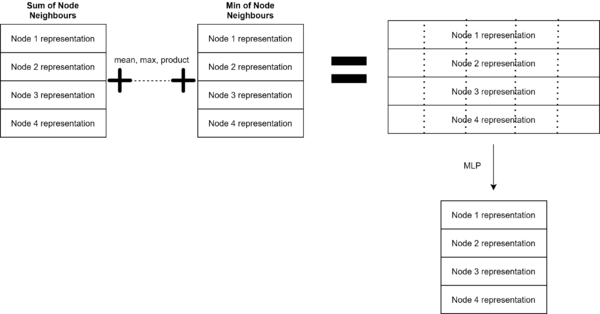
The approach for the second hypothesis is also relatively simple. Rather than compute the aggregation of the features of the neighboring nodes once, we compute the aggregation of the node features 5 times, once for each aggregation function used in hypothesis 1. Thus, we end up with 5 different node representations, one for each aggregation function. These 5 node representations are then concatenated and fed through an MLP to produce the node representation that will be used in the R-GCN. This aggregation for a graph containing 4 nodes can be seen in the figure below.

Composition of node representations from different aggregation functions

Sampling Dirichlet Priors for MLP Classification Approach

This approach is inspired by latent Dirichlet allocation which is used in document categorization. In this approach, we make the following assumptions:

1. Each node $n$ in the graph has a probability of causing its neighbors to belong to a certain class.
2. Each relation type $r$ has a probability of making the receiving node belong to a certain class.
3. Each source node $n$ with an edge of relation $r$ has a probability of making the receiving node belong to a certain class.
4. We can sample the probabilities 1,2, and 3 from their corresponding Dirichlet distribution with a vector parameter $a$ = $[a_{1}+1,a_{2}+1,...,a_{k}+1]$, note that $a_{1},...,a_{k}$ are calculated prior to training by examing the dataset.
5. Using multiple samples of probabilities 1,2, and 3, we can form a node feature for the source node. This can be seen in the second figure below for node "Brazil" with relation "lived in".

We will explore this approach by using the example in the figure below, where we will classify node User1 given its neighboring nodes.

An example in classifying a node with two neighboring nodes

For each neighboring node, we can form its feature by sampling from 3 different Dirichlet distributions as shown in the figure below.

Node feature of neighboring node "Brazil" of relation "lived in"

Each neighboring node feature is passed through two linear layers with a Relu activation function, the output for each neighboring node feature is summed, and the softmax activation is used to determine the probability for each class. We optimize the parameters of the classifier using cross-entropy loss.

Dirichlet node feature - MLP classifier

Datasets

In order to test the performance of the entity classification algorithms above, we use two knowledge graphs commonly used in benchmarking entity classification, AIFB, and MUTAG. The graphs are split into training nodes and validation nodes, using 80% of the nodes in training and 20% of the nodes in validation.

The AIFB graph contains information about the staff and publications of the AIFB research insitiute. It contains 8285 nodes, 66371 edges, 91 edge types and 4 classes. Each class corresponds to a research group at the institute.

The AIFB graph contains 4 classes, out of which 8137(98%) nodes are of a single class. Each node in the graph has from 0 to 1248 neighboring nodes, with a mean of 7.9 and a variance of 802. Removing the outliers with a high number of neighboring nodes, the mean number of neighboring nodes is 7.26, with a variance of 236.

The MUTAG graph contains information about 188 chemicals and aims to classify chemical compounds into two classes based on their "mutagenic effect on a bacterium". It contains 23644 nodes, 172098 edges and 47 edge types.

It is important to note that the MUTAG graph only contains two classes, out of which 23515(99%) nodes are of a single class. Each node in the graph has from 0 to 6784 neighboring nodes, with a mean of 7.28 neighbors, and a variance of 3114. Removing the outliers with a high number of neighboring nodes, the mean number of neighboring nodes is 6.55, with a variance of 178.

Results

	AIFB Validation Accuracy	MUTAG Validation Accuracy
R-GCN Sum	0.96	0.61
R-GCN Mean	1.0	0.67
R-GCN Min	0.54	0.52
R-GCN Max	0.64	0.57
R-GCN Composed	0.93	0.59
Dirichlet MLP	0.99	1.0

The testing was done on the 20% validation split of the graph nodes, and the classification accuracy was recorded. The classification accuracy is calculated by taking the number of correct predictions and dividing it by the total number of predictions. A prediction is correct if the argmax of the R-GCN/MLP output is equal to the label. While classification accuracy is commonly used in machine learning, it can be misleading when the majority of the dataset belongs to one class. A model that predicts by the mode of the labels will have high classification accuracy even though it is overfitted.

In the table above, it is seen that the R-GCN Mean outperforms the sum in both graphs as expected. This could be because the mean is more robust to the high variance of the number of neighboring nodes in the graphs. The R-GCN max and min perform poorly, with the R-GCN max outperforming the min in both datasets. The R-GCN composed performed better than min and max, however, it did not outperform sum and mean. While the Dirichlet MLP performs exceptionally well, is likely due to the fact that predicting by mode will yield exceptional results on both datasets, as more than 98% of the nodes belong to a single class. Additional regularization and retesting of the Dirichlet MLP will yield more realistic results.

Conclusion

The R-GCN mean was the best performer in both datasets, validating hypothesis one. The R-GCN composed did not outperform the R-GCN mean and sum, invalidating hypothesis two. Hypothesis three remains inconclusive due to the fact that the model likely overfitted and was mostly predicted by the mode. Additional testing to the Dirichlet-MLP is required to provide conclusive results.

Annotated Bibliography

Put your annotated bibliography here. Add links where appropriate.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.