Course:CPSC522/Spam Detection

Spam Detection

Spam detection is an important feature of email services. There are various anti-spam techniques, and a list of widely used techniques is discussed at Wikpedia: anti-spam techniques. Since spam detection is a binary classification problem, machine learning techniques can be well applied here. Among various machine learning algorithms, Naive Bayes is a baseline technique for dealing with spam that can tailor itself to the email needs of individual users and give low false positive spam detection rates that are generally acceptable to users . More recently, email service providers such as Google and Microsoft are try to incorporating deep learning techniques into their spam detection algorithms. So is deep learning a better approach to spam detection? We will explore this idea in this page.

Author: Yan

Abstract

In this page, we will compare Naive Bayes and Deep Belief Network in terms of spam detection task. We will first introduce some background information of Naive Bayes and Deep Belief Network. Then we describe our evaluation plan including data, details of implementation, metrics and experiment plan. Finally we present our results and give some insights based on our findings.

Build on

This page is build on Probability, Neural Network and Deep Neural Network.

Background

Naive Bayes

Probability Model

Naive Bayes (NB) algorithm applys Bayes’ theorem with the “naive” assumption of independence between every pair of features. Given a class variable $y$ and a feature vector $x_{1}$ through $x_{n}$, Bayes’ theorem states the following relationship:

$P(y|x_{1},\dots ,x_{n})={\frac {P(y)P(x_{1},\dots ,x_{n}|y)}{P(x_{1},\dots ,x_{n})}}.$

Applying “naive” assumption

$P(x_{i}|y,x_{1},\dots ,x_{i-1},x_{i+1},\dots ,x_{n})=P(x_{i}|y)$

for all $i$, we will get:

$P(y|x_{1},\dots ,x_{n})={\frac {P(y)\prod _{i=1}^{n}{P(x_{i}|y)}}{P(x_{1},\dots ,x_{n})}}.$

Since $P(x_{1},\dots ,x_{n})$ is a constant given input, we will have:

$P(y|x_{1},\dots ,x_{n})\propto P(y)\prod _{i=1}^{n}{P(x_{i}|y)}$

And this mean we can predict $y$ using:

${\hat {y}}=\arg \max _{y}P(y)\prod _{i=1}^{n}{P(x_{i}|y)}$

Parament Estimation

And the next step is to estimate $P(y)$ and $P(x_{i}|y)$. With a multinomial model, we will get:

$P(Y=y_{k})={\frac {\#D\{Y=y_{k}\}}{|D|}}$

$P(X_{i}=x_{ij}|Y=y_{k})={\frac {\#D\{X_{i}=x_{ij}\wedge Y=y_{k}\}}{\#D\{Y=y_{k}\}}}$

where $D$ is the training set.

Smoothing

If a given class and feature value never occur together in the training data, then the frequency-based probability estimate ($P(x_{i}|y)$) will be zero. This is problematic because it will wipe out all information in the other probabilities when they are multiplied. Therefore, it is often desirable to incorporate a small-sample correction, called pseudocount, in all probability estimates such that no probability is ever set to be exactly zero. In this way, $P(x_{i}|y)$ is estimated as:

$P(X_{i}=x_{ij}|Y=y_{k})={\frac {\#D\{X_{i}=x_{ij}\wedge Y=y_{k}\}+\alpha }{\#D\{Y=y_{k}\}+\alpha n}}$

where $\alpha$ is the pseudocount. If we set $\alpha$ to be 1, then it is called Laplace smoothing. Otherwise it is called Lidstone smoothing.

Deep Belief Network

Restricted Boltzmann Machine

A restricted Boltzmann machine (RBM) is a generative stochastic artificial neural network that can learn a probability distribution over its set of inputs. Its neurons must form a bipartite graph: a pair of nodes from each of the two groups ("visible" group and "hidden" group) of units may have a symmetric connection between them, and there are no connections between nodes within a group.

An example of RBM.

Deep Belief Network

RBMs can be stacked and trained in a greedy manner to form so-called Deep Belief Networks (DBN). DBNs are graphical models which learn to extract a deep hierarchical representation of the training data.

Example of a DBN.

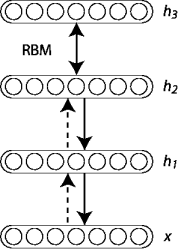
The greedy layer-wise training process if as follows:

1. Train first layer ($h_{1}$) as an RBN that use input data ($x$) as its visible layer.
2. Use that first layer to obtain a representation of the input that will be used as data for the second layer ($h_{2}$).
3. Train the second layer as an RBM, taking the transformed data (from step 2) as training examples.
4. Iterate (2 and 3) for the desired number of layers.
5. Fine-tune all the parameters of this deep architecture with respect to a supervised training criterion.

Evaluation

Data

There are some widely used spam datasets available online. We will use Enron-Spam datasets and Ling-Spam datasets. Detail statistics of these datasets are described as follows:

Name	Size	Spam Ratio	Format
Enron-Spam	36715	54.94%	Subject & Body
Ling-Spam	2893	16.63%	Subject & Body

Data Preprocessing

The first step is to clean and preprocess data. The bag of words model is simple but commonly used when dealing with text data. We apply bag-of-words model to emails and get their vector representations. However, these initial vector representations are too sparse to be feed into classifiers. Therefore we employ several feature engineering tricks here to get qualified features for classification.

Keyword List

In early years, using a keyword list is a very simple approach to identify spam.s Emails containing words in the list are considered as spam. Apparently this would lead to a lot of false positive cases, but we can apply this idea to our problem. We only count words that in the keyword list and ignore other words. Since a keyword list usually contains less than 100 words, we can significantly reduce the dimension of vector representations.

Capitalization

Another feature of spams is abuse of capitalization such as consecutive use of capital letters. The appearance of "FREE" or "PLEASE FIND US AT" is a clear warning of spams. Inspired by UCI Spambase Dataset, we also generate several feature related to capitalization, including:

• Average length of consecutive capital letters
• Longest length of consecutive capital letters
• Total length of consecutive capital letters

Subject

Subject is shorter but more important. However in bag-of-words model there is no difference between subject and body. To emphasize the importance of subject, we slight modified the bag-of-words model. Each word is subject is counted $\lambda$ times instead of 1. In our experiments we set $\lambda$ to 2.

Links

Links is another indication of spams. Therefore we also count the number of links in each email as a feature.

Experiment Settings

We random split data into training set and testing set (80 training vs 20 testing). Then we extract features mentioned above and feed them into classifiers. Details of experiment settings is listed as follows:

Naive Bayes:

• We use the implementation from scikit-learn.
• We use Laplace smoothing.
• There is no need for parameter tuning.

Deep Belief Network

• We use the implementation from nolearn.
• There is a learning rate decays after each iteration.
• We need to conduct parameter tuning for learning rate, learning rate decay, maximum number of iterations, number of hidden layers and number of nodes in each hidden layers. We only search for optimal parameters in a small range due to computational limitation.

Evaluation Metrics

The evaluation metrics that we use includes:

• Accuracy

$accuracy={\frac {truepositive+truenegative}{truepositive+truenegative+falsepositive+falsenegative}}$

• Precision

$precision={\frac {truepositive}{truepositive+falsepositive}}$

• Recall

$recall={\frac {truepositive}{truepositive+falsenegative}}$

• F1 score

$F_{1}=2*{\frac {precision*recall}{precision+recall}}$

Results

We compute classification accuracy of each classifier on each data set and the results are listed below.

	Accuracy	Precision	Recall	F1-score
NB-Enron	0.81	0.77	0.77	0.77
3-Layer-DBN-Enron	0.79	0.85	0.56	0.68
2-Layer-DBN-Enron	0.72	0.75	0.50	0.6
NB-Ling	0.71	0.68	0.68	0.68
3-Layer-DBN-Ling	0.74	0.78	0.50	0.61
2-Layer-DBN-Ling	0.68	0.71	0.42	0.53

Conclusion

If we only look at accuracy:

• NB is better than DBN when spam ratio is high and DBN is better than NB when spam ratio is low. We may conclude that DBN is more robust to change of spam ratio.
• Increasing number of layers in DBN is an efficient way to improve performance of DBN.

But in reality, false positive (an important non-spam email appears in you trash bin) is big problem because you may lose important information. While false negative (a spam email appears in your inbox) can be annoying, but do less harm. So it makes more sense to minimize false positive. With this idea:

• DBN is better than NB because it have better precision.
• Again increasing number of layers in DBN is an efficient way to improve performance of DBN.

Besides accuracy and precision, there is also points worth mentioning:

• Training for DBN is much slower than NB.
• There is almost no need for parameter tuning for NB, while parameter tuning is a huge task for DBN (This is the reason why training in DBN is slow).