Course:CPSC522/List Recommendation

List Recommendation

Hypothesis: Item-based Algorithms will perform better in list recommender system than List-based Algorithm.

Principal Author: Yu Yan

Abstract

Nowadays, lots of websites and applications provide users with the functionality to create their own lists of items. These lists can offer users more opportunities as well as assistance to find items of interest. Hence, there is the need of list recommender system to automatically recommend lists to users in order to help them find interesting items. In this page, I present a formal definition of the list recommendation problem, analyzing the lists’ properties and proposing multiple algorithms to solve the problem. The algorithms are divided into two categories based on the interaction data they utilize, denoted as list-based and item-based respectively. The assumption I made is that item-based algorithms will outperform list-based algorithms. Through extensive experiments, I will show that list-based algorithms actually outperform item-based algorithms.

Introduction

With the development of web applications and services, people are provided with more opportunities as well as assistance in order to find items of interest. Nowadays, a lot of websites provide users with the functionality to create lists of items. These lists often contain items of a specific theme, and can help users better organize items they are interested in. For example, in Amazon, a user can create a list of items which he/she is interested in buying. In Yelp, a user can create a list of Italian restaurants that he/she often visits. In Youtube, a user can create a list of videos that he/she enjoys watching. These lists are created by website users and are made public by default. They represent the wisdom of the crowd and bring an efficient way for users to explore and discover items of interest from lists created by others. If a user can find a relevant list, it is more likely that he/she can discover many interesting items from the list, compared with merely browsing or keyword searching. In this work, I want to make use of the list information and recommend to users the lists they might be interested in.

Figure 1-List examples

Figure 1 shows several examples from two popular websites. On the left-hand side are three booklists from the Goodreads website. In this website, users are able to create their own booklists, add books into the booklists, and share these booklists with other users. On the right-hand side, a board from Pinterest website is shown. In Pinterest, users are provided with the functionality to create a board, add pins from the Internet to the board, share board and follow boards created by other users.

For different websites which provide list functionality, although the objects may differ depending on websites themselves, they still have several properties in common. These properties also restrict the lists discussed in the page:

• Lists are created by users. The first property is that these lists are created by users, instead of website staff. These lists represent the wisdom of the crowd, which is also the main motivation for my work. In the list recommender system, it only recommends existing lists that are created by the users, but will not generate new lists for recommendations.
• Users can interact with both lists and items. The second property is that for the websites we consider, users can access both lists and individual items. Even if one item is not contained in any of the lists, the users should still be able to interact with it. This is crucial in that the users, lists and items together compose a tripartite graph, which leads to richer information and more heterogeneity.
• Only implicit feedback is available. The third property is that the feedback from users is implicit feedback, instead of explicit ratings. In a lot of popular websites which provide the list functionality, we are only able to know feedback information concerning clicking, viewing, favoriting, or commenting, rather than rating. These types of feedback are called implicit feedback. The reasons for this can either be users’ reluctance to give ratings, or the websites do not provide the rating function. Implicit feedback presents both opportunity and challenge for mining users’ preference, as it is easier to collected but more difficult to interpret compared with explicit ratings.

Problem Studied

In this section, I give a formal definition of the problem. Consider a set of users $U=\{u_{1},...,u_{m}\}$, a set of items $T=\{t_{1},...,t_{n}\}$, and a set of item lists $L=\{l_{1},...,l_{n}\}$. Each list in $L$ consists of items from $T$ . Let the set of lists which user $u$ has interacted with before be denoted as $L_{u}$, $L_{u}\subseteq L$, and the set of items which $u$ has interacted with before be denoted as $T_{u}$, $T_{u}\subseteq T$. Here, the feedbacks of lists and items from users are all implicit. That is, we do not know the explicit ratings, but only the boolean observations of whether $u$ has interacted with the list/item before.

Problem definition: Given $T,U,L$ for each user $u\in U$, based on $u$’s previous consumed items $T_{u}$ or previous consumed lists $L_{u}$, recommend to $u$ the top-K lists from $L$ which $u$ has not interacted with before and would be most interested in.

The main challenge of the problem comes from the fundamental property of the list, which is a set of items. We have to figure out whether should we model each list as a whole, or model each list as a combination of different items. In other words, the granularity of the model needs to be determined. If simply modelling each list as an individual, then the problem becomes very similar to conventional item recommendation. However, the set of items is a crucial part of the lists, and should not be omitted, but will improve the performance of the list recommender system. Therefore, I tried both models and the further details will be explained in Algorithm section.

Algorithm

In this section, we talk about the algorithms I have used to solve the list recommendation problem. These algorithms can be divided into two categories. The first category is based on user’s past interaction with lists, which is denoted as list-based algorithms. The second category is based on user’s past interaction with items, which is denoted as item-based algorithms.

List-based Algorithm

Figure 2-Input and output of list-based algorithms

Now let's discuss how we utilize the general list information to facilitate list recommendation. Figure 2 shows the input and output of the list-based methods. From the figure, we only need users’ previous interaction with lists, and will call this set of algorithms as list-based algorithms. The general idea is to regard each list as an individual ”item”, and apply algorithms used by conventional item recommender systems. Based on reference to previous works, the algorithms for recommender systems can be roughly divided into two types: content-based methods and collaborative filtering methods. The former ones mainly utilize explicit features of the user and items, either from metadata or using text analysis. The latter ones aim at learning the preference of a single user from past interactions of other users. In this work, I select algorithms from both categories in order to gain a deeper understanding of recommender systems, and further compare the performances of these methods.

The first two algorithms I use are regression algorithms: linear regression and logistic regression. The reasons for selecting these algorithms include that they are simple to implement, and also efficient when enough features and training examples are given. By choosing features of lists, we are able to learn the parameters of different features using Gradient descent. The optimization criteria I used there isRMSE(Root-Mean-Square Error). The regression model for predicting user’s relevant lists can be represented as:

${\hat {p}}_{ij}=u_{i}^{T}l_{j}$

${\hat {p}}_{ij}$ is the predicted rating from user $i$ to list $j$. $u_{i}$ is the feature vector learnt for user $i$, and $l_{j}$ is the feature vector for list $j$. We call these two algorithms Linear-list and Log-list.

The third list-based algorithm I used is Matrix Factorization. Matrix factorization technique has been widely used by recommender systems and has been proved to have good performance. It is especially useful when the explicit features are unknown or difficult to get. By taking the past interactions between users and lists as input, we can learn the latent factors of both users and lists using matrix factorization. Then we can use the latent factors of users and lists to predict for each user the lists he/she might be interested in. The model for predicting list relevance using the learning result from matrix factorization can be represented as:

${\hat {p}}_{ij}=x_{i}^{T}y_{j}$

${\hat {p}}_{ij}$ is still the predicted rating from user $i$ to list $j$. Here, instead of using explicit feature vectors, the latent factors are used to compute the relevance. $x_{i}$ represents the latent factor of user $i$, and $y_{j}$ represents the latent factor of list $j$. The optimization criteria I used for learning is BPR (Bayesian Personalized Ranking) and the learn method is still gradient descent , which is good for measuring the performance of binary classifiers. This algorithm is denoted as MF-list.

Below is the pseudo code for BPR learning process:

1. Procedure LearnBPR ($D_{s},\Theta$) //$D_{s}$ is all the traning pairs 
2.        initialize $\Theta$ // $\Theta$ are the parameter vector of an arbitrary model class
3.        repeat
4.             draw $(u,i,j)$ from $D_{s}$
5.             $\Theta \gets \Theta +\alpha ({\frac {e^{-{\hat {x}}_{uij}}}{1+e^{-{\hat {x}}_{uij}}}}\cdot {\frac {\partial }{\partial \Theta }}{\hat {x}}_{uij}+\lambda _{\Theta }\cdot \Theta )$
6.        until converagence
7.        return ${\hat {\Theta }}$ 
8. end procedure

Item-based Algorithm

Figure 3: Input and output of item-based algorithms

Figure 3 shows the input and output of item-based methods. Here only user-item interactions are used to find relevant lists for each user. The intuition of item-based algorithms comes from the property of the list. Since each list is composed of multiple items, the theme, and quality of a list are determined largely by the items it contains. Following this intuition, I propose two item-based algorithms to find relevant lists. For the following algorithms, I only use users’ past interactions with individual items.

The first two algorithms I used in this section are also regression algorithms, as described in the previous section. Instead of directly finding relationships between users and lists, I apply regression algorithms on users and items. After learning the feature vectors of both users and items, each time when given a list and a user, I will aggregate the feature vectors of all the items in the list to get the feature vector of the list, and then compute the relevance of the list to the user. Given a <user,list> pair, the model for computing the relevance value between user and list can be represented as:

${\hat {p}}_{ij}=u_{i}.Aggr_{k\in j}\{t_{k}\}$

Here, $t_{k}$ is the feature vector of item $k$. The $Aggr$ represents the aggregation function which is used to compute the feature vector of list $j$ by aggregating the feature vectors of all the items in $j$. When selecting the appropriate aggregation function, we need to be careful about the impact of the list size. For example, if using a linear addition, then those lists with extremely large sizes may get high priority. In this case, the impact brought by the size of the lists dominates the quality of items within the list. However, it should be the quality of items that really matters. Therefore, we need to avoid this from happening. In my current work, the $Aggr$ function I used in the experiments is average. Using the average value of item relevance to represent the list relevance can prevent the model from preferring long list. Similarly, we call these two algorithms Linear-item and Log-item.

Similar to list-based algorithms, I also used an algorithm based on matrix factorization technique for finding the relevance between users and items. After learning the latent factors of users and items, we are able to get the latent factor of each list by aggregating the item latent factors. The relevance value between each <user, list> pair can be computed as:

${\hat {p}}_{ij}=x_{i}.Aggr_{k\in j}\{z_{k}\}$

In the above equation, $z_{k}$ is the latent factor of item $k$. The aggregation function can be the same as previous $Aggr$. The optimization criteria and learn method is the same as they are in list-based algorithm part. This algorithm is denoted as MF-item.

Experiments

In this section, we talk about the experiments conducted to measure the performance of algorithms proposed in the previous section.

Data setup

Figure 4: Statistics of Goodreads Dataset before preprocessing

The dataset I used for experiments is collected from the Goodreads website. Figure 4 shows the general statistics of the dataset. As we have mentioned before, a user is able to interact with an individual item even if the item is not contained in any lists. Similarly, in Goodreads, a user can interact with books either within or without the context of booklists. Therefore, the books in this dataset come from two sources: one is lists and another is users’ bookshelves.

Figure 5 - GoodReads dataset

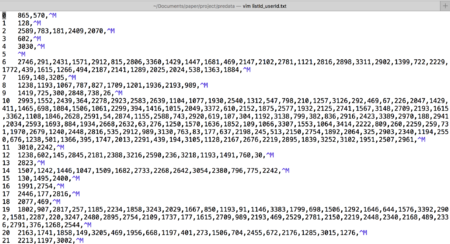
Figure 5 is the screenshot of part of the dataset, it shows the relationship between users and the list. To prevent the dataset from being too sparse, I filtered out the users with fewer than three list interactions and the lists with fewer than three user votes.

For regression algorithms, we will need the features of items and lists. The features I used are listed as below:

List features: number of books, number of voters, number of likes, relevant genres;

Book features: number of ratings, number of reviews, average rating, relevant genres.

Since the website allows users to define genres by themselves, the genres are very disorganized and many have duplicates. Therefore, I manually categorized all the genres on the website into 12 genres and used a vector to represent the genre information.

For matrix factorization methods, when learning the model, each time apart from sampling one positive instance from the training data, I also sampled one negative instance from those that do not appear in training data. The good thing of doing so is to prevent the model from always predicting high relevance. However, it also has some issue which will be discussed in our experiment analysis.

Experiment Metric

The measure metric I used is AUC, which is Area Under the Receiver Operating Characteristic. The Receive Operating Characteristic (ROC) is a graphical plot that compares the true positive rate and false negative rate. It is good for illustrating the performance of binary classifiers. The AUC metric can be represented as:

${\frac {1}{|D_{s}^{test}|}}\sum _{(u,l_{i},l_{j})\in D_{s}}\mathbf {1} ({\hat {p}}_{ui}>{\hat {p}}_{uj})$

Here $D_{s}$ represents all the triples where $<u,l_{i}>$ is a positive instance and $<u,l_{j}>$ is a negative instance. Each time for one positive instance and one negative instance for the same user from $D_{s}$ will be sampled and compared. If the relevance value between $u$ and $l_{i}$ is larger or equal to that of $u$ and $l_{j}$, it will be regarded as a successful prediction and the AUC value will add 1. Otherwise it is regarded as failure and the AUC will not get any gain. Therefore, the higher value of AUC, the better performance the recommender system has.

Experiment Results and Analysis

Each algorithm was run for 5 times on Goodreads dataset and plotted the AUC results.

Figure 6: Experiment Results under 5 Runs

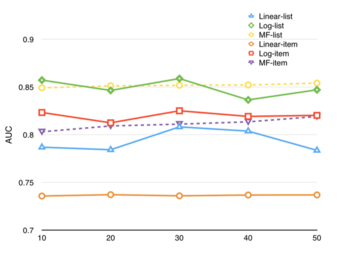
Figure 6 shows the AUC results from 5 runs. For regression algorithms, the settings among 5 runs are the same. For methods using matrix factorization techniques, the dimensionality of latent vectors increases from 10 to 50. This is to show how the dimensionality of latent factors affect the AUC result. From the results shown in Figure 5 we can get several conclusions:

• The overall performance of list-based algorithms is better than that of item-based algorithms. I think the reason for this is that the explicit features I used for the problem is strong and closely related to the list recommendation problem. Particularly, the genre vector is very useful in that it accurately captures the taste of different users and the theme/topic of different lists. Another reason for the unsatisfying performance of item- based algorithms might be the aggregation function I selected, which is the average. Although the average function prevents the list relevance from being overwhelmed by the list size, it loses the list size information at the same time. A longer list might contain more relevant items and thus the list size should not be completely ignored.
• The logistic regression algorithm performs slightly better than matrix factorization algorithms when the dimensionality of latent factors is low, and the linear regression algorithm has the worst performance. I think the reason is three-fold. First, my selection of explicit features is appropriate, and logistic regression is able to produce accurate results. Second, the interpretation of implicit feedback is not very appropriate, and matrix factorization algorithms do not perform as good as we expected. In my experiment, since I only have positive instances, I actually treated the instances which do not appear in the training data as negative instances. However, they are better regarded as unknown rather than negative, since there is potential for them to be explored in the future. Third, linear regression does not performance as good as the logistic regression in that the latter is more suitable for binary classification problem, as the possible outcomes are limited to either 0 or 1.
• The performance of matrix factorization algorithms increases as the dimensionality of latent factors increases. This is intuitive since latent factors with higher dimensionality are able to represent the objects with higher accuracy.

In general, the performances of the 6 algorithms are satisfying, as they are all able to achieve high AUC values. However, there is still room for improvement as none of them is able to achieve AUC higher than 0.9. Especially for item-based algorithms, whose performances are much worse than we expected. Also, for the two matrix factorization methods, both of them are able to converge quickly within 10 iterations. The following section will further talk about future work directions.

Future Works

In this section, I propose potential future work directions for the list recommendation work. More specifically, these would be ways to improve my item-based algorithms or list-based algorithm.

1. I would like to incorporate order of items within a list. Currently, my list recommendation work is more like set recommendation since the definition of ”list” has an inherent property of order. The motivation for incorporating order is that the order reflects the significance of items in some sense. Also, if an item ranks high in a list, it is likely that the theme or quality of the item is very close to the theme or quality of the list. In other words, items with higher ranks are more representative of the list than items ranked lower. Given the order in the lists, we are able to add weights to the items based on their positions within the list. This will be helpful when measuring the importance as well as the relevance of each individual item.
2. I would like to try different aggregation functions for item-based algorithm, since now I am only using average aggregation which does not yield good results. I also want to try different optimization criteria besides AUC.

Conclusion

As lists are becoming increasing popular, it is interesting as well as useful to build recommender system for lists. In this page, I made the assumption that item-based algorithms will work better than list-based algorithms. I first analyze the important factors for list recommendation. Based on these factors, I divide the algorithms into two categories, list-based, and item-based. List-based algorithms focus on users' past interaction with only lists while item-based algorithms focus on users' past interaction with only items. For each type of algorithm, I further propose algorithms using either explicit features or implicit features. Experiments are conducted to compare the performance of different algorithms and I present the experimental results along with analysis. The result shows that list-based algorithms have a better performance than item-based algorithms.