Course:CPSC522/Recommendation System using Matrix Factorization

Recommendation System using Matrix Factorization

Referenced Paper

1. Matrix Factorization Techniques for Recommender Systems

2. Two-level matrix factorization for recommender systems

Overview

This paper discuss the fundamental knowledge regarding recommendation system with two prerequisite algorithm called collaborative filtering and content-based filtering. Then we introduce a newer approach called matrix factorization based on the first paper "Matrix Factorization Techniques for Recommender Systems", which first proposed using matrix factorization to best utilize the matching between user current marking with related unknown to-be marked items. Then we introduced a two-level matrix factorization, which is based on the previous paper to have two-level processing network which greatly improves prediction accuracy.

Abstract

Nowadays, with growing popularity of people getting used to use Internet for their daily information search and digest, we have already been using a lot of tools that help us to better get the exact information that we need. Search engines like Google greatly give people convenience in improving users' capacity in providing user with lots of information they want using user specific keywords. However, except for positively seeking information, many companies provide personalized recommendation system to help people make better decision based on their previous searching, looking or buying experience such as Amazon for online shopping and Netflix for movie recommendation, etc. Here we are going to give a brief introduction towards the recommendation system as well as currently the best algorithm framework for recommendation system called matrix factorization as well as improved version of matrix factorization called two-level matrix factorization system.

Builds on

Automatic recommendations are generated by previous user profile as well as filtering and learning algorithms. Basic approaches are based on collaborative filtering[1] and content-based filtering[2].As for this page, we are proposing the recommendation system based on matrix factorization which has already been implemented by Netflix and has already been a big success.

Related Pages

Recommendation system involves learning and filtering algorithm including collaborative filtering[3] and content-based filtering[4] as well as hybrid recommender system[5]

Background

It is assumed that reader should have background knowledge regarding basic probability and equivalent mathematical background.

Recommendation System

Introduction

Recommendation system or so called recommender system derives from previous information filtering system which aims to provide user with automatic prediction of rating or preference[6], where the suggestions relates to different decision-making process including buying items, choosing what music to listen or which book to read. With the rapid growing popularity of Netflix, an online video website, which provides user with user-specific video recommendation for different choice, recommendation system has attracted wide public attention and increasing research topic. Currently, recommendation system is mainly consisted within these two main approaches: collaborative filtering and content-based filtering[7]

Prerequisite

Collaborative filtering

Collaborative filtering is based on the using history of user behavior which specifically refers to user's past watching, listening or purchasing history record that can be compared with other users making similar decision, which means that if a person A has the same opinion as a person B on an issue, A is more likely to have B's opinion on a different issue x than to have the opinion on x of a person chosen randomly. For instance, we can make a recommendation system for predicting people's taste on television with likes or dislikes but these predictions also aims for targeted user which are gathered from a lot of other users, which is a little bit different from simply giving an average score for items. In general, it can be concluded that collaborative filtering is the process of filtering for information or patterns involving multiple agents collaborating with each other and popular application regarding collaborative filtering is mainly connected with large large data sets mining. Typically, a collaborative filtering system can be implemented into the following two steps:

1. Regarding the current active user, use the system to find those people who share the same rating pattern with the current user
2. Utilize those rating of users from system to calculate a prediction for the current user.

There is another collaborative filtering technique called item-based collaborative filtering which resembles the previous two steps:

1. Build an item-item matrix determining relationships between pairs of items
2. Infer the tastes of the current user by examining the matrix and matching that user's data[8]

This image shows an example of predicting of the user's rating using collaborative filtering. At first, people rate different items (like videos, images, games). After that, the system is making predictions about user's rating for an item, which the user hasn't rated yet. These predictions are built upon the existing ratings of other users, who have similar ratings with the active user. For instance, in our case the system has made a prediction, that the active user won't like the video.

Content-based filtering

Content-based filtering, which can also be called cognitive filtering, is a kind of recommendation algorithm which recommends items based on a comparison between the item content and the profile of a user. Each item content is consisted of a series of descriptors and terms which can be the occurrence of words in a book. The user profile can be represented with the same terms and constructed by analyzing the content of items. Content-based filtering is mainly associated with text documents because a standard approach for parsing a single words from documents are from them. For the text filtering,vector space model and latent semantic indexing are frequently used to identify documents in vectors in the multi dimensional space. Regarding the implementation of content-based filtering, we can choose the terms to be assigned automatically or manually When terms are assigned automatically a method has to be chosen that can extract these terms from items. Second, the terms have to be represented such that both the user profile and the items can be compared in a meaningful way. Third, a learning algorithm has to be chosen that is able to learn the user profile based on seen items and can make recommendations based on this user profile A typical content based filtering can be handled by the following three component:

1. Content analyzer: When it comes for non-structural processing including text, pre-processing is needed to generate relevant structural information. Content analyzer is used to represent the content of items (e.g. documents, Web pages, news, product descriptions, etc.) coming from information sources in a form suitable for the next processing steps. Feature extraction is used for items to shift item representation from the original information space to the target one and the result is used as the input for profile learner and filtering component.
2. Profile learner: Profile learning is used to collect data characteristics from user preferences and generalize them to construct the user profile. The common generalization strategy is implemented by machine learning which are able to infer a model of user interests starting from items liked or disliked in the past.For instance, a web page recommender can implement a relevance feedback method where the learning strategy combines positive and negative vectors example into a prototype vector representing the user profile. Training examples can be Web pages where a positive or negative feedback is provided by the user.
3. Filtering component: It helps to find out the user profile to suggest relevant items by matching the profile representation. The result is a binary or continuous relevance judgment. When it is a continuous relevance judgement, it will result in a ranked list of potentially interesting items.

Content-based Recommendation Architecture ]

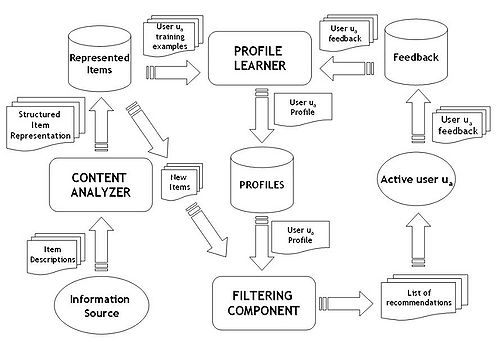Real Application: Genome Project

The Music Genome Project was first conceived by Will Glaser and Tim Westergren in late 1999. In January 2000, they joined forces with Jon Kraft to found Savage Beast Technologies to bring their idea to market.The Music Genome Project is an effort to "capture the essence of music at the most fundamental level" using over 450 attributes to describe songs and a complex mathematical algorithm to organize them. The Music Genome Project is currently made up of 5 sub-genomes: Pop/Rock, Hip-Hop/Electronica, Jazz, World Music, and Classical. Under the direction of Nolan Gasser and a team of musicological experts, the initial attributes were later refined and extended.

A given song is represented by a vector containing values for approximately 450 "genes" (analogous to trait-determining genes for organisms in the field of genetics, although it has been argued that this methodology bears greater resemblance to phylogeny). Each gene corresponds to a characteristic of the music, for example, gender of lead vocalist, prevalent use of groove, level of distortion on the electric guitar, type of background vocals, etc. Rock and pop songs have 150 genes, rap songs have 350, and jazz songs have approximately 400. Other genres of music, such as world and classical music, have 300–450 genes. The system depends on a sufficient number of genes to render useful results. Each gene is assigned a number between 0 and 5, in half-integer increments. The Music Genome Project's database is built using a methodology that includes the use of precisely defined terminology, a consistent frame of reference, redundant analysis, and ongoing quality control to ensure that data integrity remains reliably high.

Given the vector of one or more songs, a list of other similar songs is constructed using what the company calls its "matching algorithm". Each song is analyzed by a musician in a process that takes 20 to 30 minutes per song.Ten percent of songs are analyzed by more than one musician to ensure conformity with the in-house standards and statistical reliability.

One Level Matrix Factorization

Recommendation system using matrix factorization was first proposed by Netflix and therefore, has been widely used and known to people due to its outstanding performance and accuracy recommendation comparing to other methods. So we are going to discuss this in detail in the following paragraph

Basic introduction

Matrix factorization is one model of collaborative filtering called latent factor model which predicts user and item's overall structure within latent factors. From an overall perspective, user preference to an item can be estimated by multiplication of decomposed user and item latent factors and it is clear that matrix factorization is obviously the process to factorize a matrix by finding out two matrices when you multiply them, you can get the original matrix. From this perspective, we can infer that using the above property, matrix factorization can be used to find out the underlying interaction between two different objects or more if you apply more than two matrices, which can be used to predict the collaborative filtering rating. Let's the the example from Netflix, as we are most familiar with. Suppose there exists a group of users with a group of items, which can be the movie for the system. Every user in the system rates several items in the system and we want to see how those users can predict items they haven't predict based on their previous rating records, which can be seen as another form form automatic recommendation. In this circumstance, we can represent and map all our information into a matrix as the following picture. Currently, we have five users and ten items with the rating standard starting from 1 to 5 where 1 is least and 5 is the strongest recommendation.

	D1	D2	D3	D4
U1	5	3	-	1
U2	4	-	-	1
U3	1	1	-	5
U4	1	-	-	4
U5	-	1	5	4

As can be inferred from the above table, we can infer that predicting the missing ratings in the table is equivalent to filling the blanks so that the predicted value will be consistent with current ratings in the system. We can assume that two users will give the same movie high ranking if they both like the movie with their preferred movie genre like action, comedy movie, etc, which we can call this as latent features. If we can discover the features, we can then try to predict a rating regarding a certain item of a certain item because the feature associated with the user should match the features associated with them. In order to finish the task, we will make assumptions that the number of features would be smaller than user number and its respective items, which can be easy to reason about in the first place. So let's see how we can discuss and discover matrix factorization using mathematics.

Discovering matrix factorization using mathematics

Suppose we have a set of users $U$ and a set of items $D$. We assume $R$ is the size of $|U|*|D|$ to be the matrix that contains all the assigned item ratings. Furthermore, we also assume that we would like to discover $K$ latent features, which is equivalent to find two matric matrices $P(a|U|*K_{matrix})$ and $Q(a|D|*K_{matrix})$ so that the output approximates

                                                                     $R=P*Q^{t}=R$

Then each row of $P$ can represent the strength of associations between a user and the features where $Q$ can represent the strength of associations between an item and the features. In order to predict an item rating $d_{j}byu_{i}$, it can be calculated the dot product of two vectors responding to the $u_{j}{i}$ and $d_{j}$:

                                                                     $r_{ij}=p_{i}q_{j}=\sum _{k=1}^{k}p_{ik}q_{kj}$

Next we can obtain $P$ and $Q$ by initializing the two matrices with some values and calculate how different their product is comparing to M and try to minimize the different recursively, which is known for gradient descent descent to find local minimum difference by the following formula:

                                                                     $r_{ij}^{2}=(r_{ij}-r_{ij})^{2}=(r_{ij}-\sum _{k=1}^{K}p_{ik}q_{kj})^{2}$

To minimize the error, in gradient descent, we need to know in what direction we need to go to get the minimum value of $p_{ik}$ and $q_{kj}$, which we can also call this as the current values, so we need to know the below two variables separately:

                                                                     $\textstyle {\frac {\theta }{\theta _{pik}}}e_{ij}^{2}=-2(r_{ij}-r_{ji})(q_{kj})=-2e_{ij}q_{kj}$

                                                                     $\textstyle {\frac {\theta }{\theta _{pik}}}e_{ij}^{2}=-2(r_{ij}-r_{ji})(q_{ik})=-2e_{ij}q_{ik}$

When we obtained the gradient, we can then formulate the $p_{jk}$ and $q_{kj}$

                                                                     $p_{ik}=p_{ik}+\theta \textstyle {\frac {\theta }{\theta _{pik}}}e_{ij}^{2}=p_{ik}+2\alpha e_{ij}q_{kj}$

                                                                     $q_{kj}=p_{kj}+\theta \textstyle {\frac {\theta }{\theta _{qkj}}}e_{ij}^{2}=q_{kj}+2\alpha e_{ij}q_{ik}$

We usually choose $\alpha$ as 0.0002 as it is a constant value to determine the minimum rate of approaching and if we choose the value too large, we may end up not being able to reach the minimum and just turning around the minimum.

After we get this, we can then recursively perform the operation until we reach the minimum error coverage rate with the following formula

                                                                     $\sum _{(u_{i},d_{j},r_{ij})\in T}e_{ij}=\sum _{(u_{i},d_{j},r_{ij})\in T}(r_{ij}-\sum _{k=1}^{K}p_{ik}q{kj})^{2}$

Matrix Factorization in Python

When we understand the mathematical derivation process of matrix factorization, we won't be difficult for us to understand the implemention in high-level language:

   1 import numpy
   2 def matrix_factorization(R, P, Q, K, steps=5000, alpha=0.0002, beta=0.02):
   3 Q = Q.T
   4 for step in xrange(steps):
   5     for i in xrange(len(R)):
   6        for j in xrange(len(R[i])):
   7            if R[i][j] > 0:
   8                eij = R[i][j] - numpy.dot(P[i,:],Q[:,j])
   9                for k in xrange(K):
   10                   P[i][k] = P[i][k] + alpha * (2 * eij * Q[k][j] - beta * P[i][k])
   11                    Q[k][j] = Q[k][j] + alpha * (2 * eij * P[i][k] - beta * Q[k][j])
   12    eR = numpy.dot(P,Q)
   13    e = 0
   14    for i in xrange(len(R)):
   15        for j in xrange(len(R[i])):
   16            if R[i][j] > 0:
   17                e = e + pow(R[i][j] - numpy.dot(P[i,:],Q[:,j]), 2)
   18                for k in xrange(K):
   19                   e = e + (beta/2) * (pow(P[i][k],2) + pow(Q[k][j],2))
   20    if e < 0.001:
   21        break
   22 return P, Q.T

Let's use some real data input and see actual result:

   R = [
    [5,3,0,1],
    [4,0,0,1],
    [1,1,0,5],
    [1,0,0,4],
    [0,1,5,4],
   ]
  R = numpy.array(R)
  N = len(R)
  M = len(R[0])
  K = 2
  P = numpy.random.rand(N,K)
  Q = numpy.random.rand(M,K)
  nP, nQ = matrix_factorization(R, P, Q, K)
  nR = numpy.dot(nP, nQ.T)

And the actual result is like this comparing to the previous table we have. As you can see, we use the gradient descent to calculate all the numbers that we need

	D1	D2	D3	D4
U1	4.97	2.98	2.18	0.98
U2	3.97	2.40	1.97	0.99
U3	1.02	0.93	5.32	4.93
U4	1.00	0.85	4.59	3.93
U5	1.36	1.07	4.89	4.12

We can see that the values are very close to the real values in the previous table and we predict the unknown values as we have already planned. It is quite clear that using matrix factorization can generate high-accuracy prediction data.

Two Level Matrix Factorization

Why do we need two-level matrix factorization

As for now, current matrix recommendation system including the current one Netflix has been using will encounter cold start problem, which is related to the issue that the system cannot draw any reference for users or items when it has not been yet gathered enough information for now. This problem is especially prevalent in recommendation system. A recommendation system compares the user's profile to some reference characteristics and these characteristics may be from the information item (the content-based approach) or the user's social environment (the collaborative filtering approach). In the content-based filtering, Characteristics of an item must be matched with the features with user's profile. Therefore, it is necessary to from the very start to construct a sufficiently-detailed model of the user's tastes and preferences through preference elicitation which can be achieved by querying the user or observing the user's behavior. As a result of this, the cold start problem is that the user has to dedicate a certain amount of time to initialize the system from construction of user profile.

What are the heuristic

• Propose weighted textual matrix factorization to compute the semantic similarities between items
• Propose a two-level matrix factorization model by providing textual item semantic relations and users' subjective rating preference together.
• Generate two-level matrix factorization

Prerequisite

Textual Semantic Similarity: Textual semantic similarity is a metric to define the distance of different textual documents and the distance distance between them is based on the likeness of their meaning or semantic content as opposed to similarity which can be estimated regarding their syntactical representation. Mathematical tools can be utilized to estimate the semantic relationship between different textual documents by numerical descriptions by comparison with the relevant information supporting their meaning or describing their nature. When it is considered for recommendation system, it could be very important since most of the current recommendation system model didn't fully utilize this aspect

Weighted textual matrix factorization: WTMF model has been widely adopted in NLP field and its main contribution is that the missing words are modeled to greatly enrich the features of sentences and short text. WTMF models sentences by textual matrix factorization method that considers missing words as additional constraints for semantics of sentences. Furthermore, textual matrix factorization is applied mainly on the term-document matrix.

Implementation

The system first calculates the semantic relations between items with textual matrix factorization and then combine items' semantic relations and users' rating preference into two-level matrix factorization model where the semantic relations within items are analyzed by lower-level matrix factorization to make up of the lack informative rating knowledge and user's subjective rating preference is combined into the upper-level matrix factorization.

Two-level matrix factorization model architecture

As can be seen from the left diagram for the overview architecture of the two-level matrix factorization, two level matrix factorization first does computation on the semantic relations between items according to the textual matrix factorization and then are embedded into the two-level model called TLMF. TLMF is a combined model based on one-level matrix factorization and it takes both the rating matrix but also the relations between the items and the account. Both of the relations are modeled into a unified learning model with three limitations:

• The learned rating values need to be as close as to the observed rating values.
• The lower-level textual matrix factorization models are redesigned into model relations between words and sentences by providing impact of missing words to improve semantic analysis performance.
• Mapping computation can be optimized by minimizing the regularized squared error.

There is the pseudo-code for this algorithm:

 Input: R: the user-item rating matrix.
 d: the dimension of latent feature vector on upper level.
 K: the dimension of latent feature vector on lower level.
 T: the textual corpus of items.
 Z: the number of iterations.
 λ: the regularization parameter for upper level MF.
 γ: the regularization parameter for lower level MF.
 η: the learning rate.
 wm: the parameter of missing words.
 Output: P: the user latent feature matrix.
 Q: the item latent feature matrix.
 1 Build term document matrix with TF*IDF values based on textual corpus of items T
 2 Initiate A0 and B0 with random decimals and j=0
 3 while j < Z or (Lj - Lj+1 ≤ C) do
 4 	for all words and sentences
 5 		Compute and update A and B by Eqn. 10 and 11
 6 	end for
 7 j++
 8 end while
 9 Compute similarity matrix S by Eqn. 9
 10 Initiate P0 and Q0 with random decimals and j=0
 11 while j < Z or (Lj - Lj+1 ≤ C) do
 12 	for all users and items
 13 		Compute and update P and Q by Eqn. 13 to 16
 14 	end for
 15 j++
 16 end while
 17 return P and Q

Result

Two Level Matrix Factorization Result Comparing With Other Benchmarks

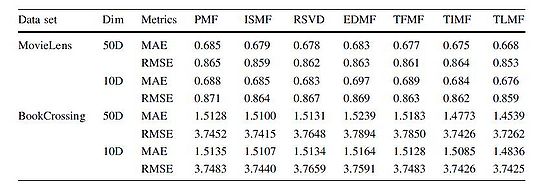It is quite clear the result of the proposed method comparatively reduce the MAE and RMSE with about 3% with respect to the other 6 benchmarks.