Course:CPSC522/Learning Probabilistic Models with Complete Data

Learning probabilistic models with complete data

Learning probabilistic models with complete data usually refers to finding density estimation for that model given all the values of the variables in the model.

Principal Author: Ainaz Hajimoradlou

Abstract

This page discusses how to learn probabilistic models with complete data meaning that all the values of the variables in the model exist. This is simply approximating a probability density function for the given data such that for every sampled data point in the sample space there is a relative likelihood of what that data point is going to be.

Builds on

This page builds on principle concepts of probability theory such as conditional probability and Bayes rule. It then moves on how to learn Bayesian structures and investigate cases where the model of the data is not available. At the end density estimation for non-parametric models is explained base on algorithms such as k-nearest neighbours and kernel functions.

Related Pages

Bayesian networks are most common approach for learning probabilistic models.

Probability theory is the essence for understanding how probabilistic models are learned.

Content

Introduction

Probability is a measure to show how likely an event is. Therefore, each event can be measured by probability. If two events are independent, then the joint probability of them can be obtained by simply multiplying them. As, the occurrence of one event does not depend on the other one.

$P(A\land B)=P(A\cap B)=P(A)P(B)$.

In most cases, we want to obtain the probability of an event given some hypothesis. The following is the conditional probability. It is obvious that in a case where $P(B)=0$, conditional probability is not defined. Because, we are conditioning on something which is not likely to occur.

$P(A\mid B)={\frac {P(A\cap B)}{P(B)}}$

One of the key concepts in maximum likelihood learning is chain rule. Taking into account the conditional probability, we can always calculate the joint probability of an indexed collection of sets $A_{1},A_{2},...,A_{n}$ as following:

$P(\bigcap _{i=1}^{n}A_{i})=\prod _{i=1}^{n}p(A_{i}\mid \bigcap _{j=1}^{i-1}A_{j})$

Based on these concepts, we first examine maximum likelihood learning on both continuous and discrete data and then move on to more complicated cases with non parametric models.

Motivation

Although data is not complete in most real world problems, it is good to know how to solve a simpler problem to understand the basics. This is equal to converting more complicated problems to simpler ones of which we know how to solve.

Maximum likelihood parameter learning

In Bayesian learning, we calculate the probabilities of hypothesis, given the data, and make predictions based on all of them . If $d$ is the observed value of data $D$ and $h_{i}$ is the hypothesis, we have:

$P(h_{i}\mid d)=\alpha P(d\mid h_{i})P(h_{i})$

$P(d\mid h_{i})$ is the likelihood of the data under each hypothesis and $P(h_{i})$ is the hypothesis prior.

For prediction of an unknown quantity, by assuming that each hypothesis has a probability distribution over X, we have: $P(X\mid d)=\sum _{i}P(X\mid d,h_{i})P(h_{i}\mid d)=\sum _{i}P(X\mid h_{i})P(h_{i}\mid d)$

Discrete models

Suppose we have a box of chocolates with two different flavours and we want to find the proportion of chocolates with flavour 1. If $\theta$ is the proportion of the chocolates with flavour 1 and its corresponding hypothesis is $h_{\theta }$, by assuming that all proportions are equally likely, we can use maximum likelihood approach to model the data. By observing $\mathbb {N}$ different chocolates, if $n_{1}$ of them has flavour 1 and the rest ($n_{2}=N-n_{1}$) has flavour 2, we can write:

Figure 1. Bayesian network for the box of chocolates with flavour 1.

$P(d\mid h_{\theta })=\prod _{j=1}^{n}P(d_{j}\mid h_{\theta })=\theta ^{n_{1}}(1-\theta )^{n_{2}}$

Finding the derivative of this function may seem a bit hard. Therefore, we calculate the log likelihood which is shown by $L$.

$L(d\mid h_{\theta })=\sum _{j=1}^{n}log(P(d_{j}\mid h_{\theta }))=n_{1}log(\theta )+n_{2}log(1-\theta )$.

Setting derivative to zero results in $\theta ={\frac {n_{1}}{n_{1}+n_{2}}}={\frac {n_{1}}{N}}$. Which is the best $\theta$ that gives the maximum likelihood. Figure 1 shows the Bayesian network for this example.

These results imply that the actual proportion of the chocolates with flavour 1 is equal to the proportion of them that have been observed so far. This has some obvious problems for small datasets. If the dataset is small enough, then it is likely that we don't observe chocolates with flavour 1 which results in having a proportion of zero for this flavour which is not right. In order to avoid these kinds of problems, we can use pseudo counts. We can add more parameters to the problem and calculate the probability by Bayes rule. Then, by calculating the log likelihood, obtain the best parameter to achieve maximum likelihood. An example can be adding a variable like colour to the box of chocolates and calculating the probability of chocolates with flavour 1 and colour x.

Continuous models

Continuous models are usually modelled using Gaussian functions. Consider a probability density functions as follows from which the data is generated:

$P(x)={\frac {1}{{\sqrt {2\pi }}\sigma }}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$

As it is shown, the parameters of the model are $\mu$ and $\sigma$. In order to find these parameters, we must calculate the derivative of the log likelihood (similar to discrete data) and set it to zero. If we observe $N$ values of $x$, the following is the log likelihood:

$L=\sum _{j=1}^{N}{\frac {1}{{\sqrt {2\pi }}\sigma }}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}=N(-log{\sqrt {2\pi }}-log\sigma )-\sum _{j=1}^{N}{\frac {(x_{j}-\mu )^{2}}{2\sigma ^{2}}}$

Setting the derivatives to zero:

${\frac {\partial {L}}{\partial {\mu }}}=-{\frac {1}{\sigma ^{2}}}\sum _{j=1}^{N}(x_{j}-\mu )=0\rightarrow \mu =\sum _{j}{\frac {x_{j}}{N}}$

${\frac {\partial {L}}{\partial {\sigma }}}=-{\frac {N}{\sigma }}+{\frac {1}{\sigma ^{3}}}\sum _{j=1}^{N}(x_{j}-\mu )^{2}=0\rightarrow \sigma ={\sqrt {\sum _{j}{\frac {(x_{j}-\mu )^{2}}{N}}}}$

As expected, the maximum likelihood of the mean and the standard deviation are equal to the sampled average and the square root of the sampled variance respectively.

A more interesting case with gaussian function is when it is used for modelling the noise of linear models in supervised learning. If $X$ is the training data and $y$ is the corresponding labels, having $P(y_{i}\mid x_{i},w)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {(w^{T}x_{i}-y_{i})^{2}}{2}}}$ where $\mu =0,\sigma =1$ and $w$ is the learned weight of the model, we can derive to the squared loss using negative log likelihood.

Different continuous functions result in different loss functions. For example, Laplace likelihood gives us the absolute error and the sigmoid likelihood results in binary logistic loss.

Bayesian parameter learning

As you recall we had some major problems with maximum likelihood learning. In the previous example (box of chocolates), unless we observe a chocolate with flavour 1, $P(\Theta )$ stays zero which is not a reasonable answer. In order to solve this, Bayesian's approach is defining a prior probability distribution over different hypotheses which is called the hypothesis prior . Taking this into account, $\theta$ is the value of a random variable $\Theta$ that defines the hypothesis space and thus, $P(\Theta )$ is the hypothesis prior. For $\theta$ to be any value between 0 and 1, the prior should be a continuous function that is nonzero between 0 and 1 and zero otherwise. It should also integrate to one. We will use beta distributions for hypothesis prior and examine some of their properties.

Beta distribution

Figure 2. Beta distribution with different values of a and b.

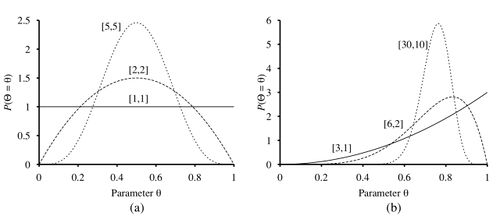
Beta distribution consists of two hyper parameters $a$ and $b$ such that:

$beta[a,b](\theta )=\alpha \theta ^{a-1}(1-\theta )^{b-1},\theta \in [0,1]$

In order to make the distribution integrate to 1, a normalization constant like $\alpha$ should be defined. This normalization constant depends on both $a$ and $b$.

Figure 2.b shows different beta distributions with equal ratio of ${\frac {a}{a+b}}$. As you can see, larger values of $a$ suggests that $P(\theta )$ is closer to 1 than 0. Figure 2.a shows different beta distributions with different values of $a+b$. Larger values of $a+b$ makes the peak of the plot higher, suggesting that we have more confidence in the values of $\theta$. Besides, beta distribution is closed under update. Meaning that if we have a prior $beta[a,b]$, after observing a data point, the posterior is also $beta[a,b]$. Thus, theses properties make this distribution an ideal choice for a hypothesis prior. $a$ and $b$ control how the distribution works. Beta distribution always gives us a probability between 0 and 1. ${\frac {a}{a+b}}$ is the average returned probability. If we set the value of $a$ and $b$ to 1, beta distribution is equal to the uniform distribution.

Figure 3. Beta[81, 219], Expected batting average for a baseball player example.

For an intuition of why beta distribution may be useful, consider this example. We want to predict the batting average of a baseball player. Batting average is simply the number of times the player gets a base hit divided by the total number of times that he goes up to bat. Batting average is clearly a number between 0 and 1. In general, most players have a batting average of 0.266. Therefore, 0.3 is considered a great record. As we have covered maximum likelihood learning so far, we know that using only previous records is not enough for predicting the batting average. Because, the player may have gotten lucky after 3 or 4 hits and using this information for predicting his batting average during the season results in an average of 1 which is unlikely (average is 0.266).

The perfect prior hypothesis in this case would be beta distribution. We expect the batting average be around 0.27 (according to the statistics). Thus, we can expect a range of 0.2 to 0.35 that is reasonable. This corresponds to $beta[81,219]$. The reason is that we know the average should be 0.27 meaning that ${\frac {a}{a+b}}=0.27\rightarrow {\frac {81}{81+219}}=0.270$. Another reason is that theses values of $a$ and $b$ will give us a distribution over $[0.2,35]$ that we wanted. Figure 3 shows the plot with these value. Y axis represents the probability density and X axis is the batting average which is also a probability. So, beta is a probability distribution over probabilities .

The curve should be updated by the number of times that the player goes up to bat. It can be proved that adding the new information is equivalent to plotting $beta[a+hits,b+misses]$ (conjugate prior). The more information is received, the more confident the results are. After 300 bats of which 100 are hits, the plot will be thinner and more peaked in comparison with figure 3. The expected value of beta distribution is ${\frac {81+100}{81+100+219+200}}=0.303$. If we only used previous results to predict the batting average, we would end up with ${\frac {100}{300}}=0.333$ which is higher than what we obtained from beta distribution. It is also important to notice that the average we obtained is higher than the average we started with (${\frac {81}{81+219}}=0.270$). Therefore, we can simply use this distribution for our previous example (box of chocolates) as well. Every time we see a chocolate with flavour 1, we increment $a$. Otherwise, we increment $b$.

Learning Bayes net structure

So far, we have considered cases where we know what the model of the data is. In most cases, we don't know the model. In this section, we will consider two approaches briefly. First approach may be searching for the model which is the obvious solution. We can start with one node and gradually add more parents and links between variables of the model. Or we can start with an initial model and then improve it with algorithms like hill climbing and simulated annealing to find a relatively good model. The model should not contain circles and we can search over possible orderings as well.

We know that we have reached a good model when either of these conditions is satisfied: testing whether conditional independence implicit in the model is actually satisfied or examining how much the model explains data. In order to avoid a fully connected graph, we have to penalize model complexity. MAP subtracts a penalty from the likelihood of each structure, while Bayesian approach samples over joint structures and parameters. MCMC is most often used for this purpose.

Density estimation with non parametric models

We can learn a probability density function without making any assumptions about the structure of the model. This is usually done in continuous domains. K-nearest neighbours is one of these models. However, choosing an appropriate value of k is not easy. If we choose a k that is very small, we will end up with a model that is too spiky. Alternatively, if we choose a very big k, the model will be very smooth. So, choosing a good value of k is tricky. Another approach is using kernel functions. In this model, we assume that each data point has its own density function. Thus, the estimated density at every point is the average density over kernels. Usually, the kernel function is a Gaussian. In this case, it is a Gaussian with standard deviation $w$ along each axis .

$P(x)={\frac {1}{N}}\sum _{j=1}^{N}\kappa (x,x_{j}),\quad \kappa (x,x_{j})={\frac {1}{(w^{2}{\sqrt {2\pi }})^{d}e^{-{\frac {D(x,x_{j})^{2}}{2w^{2}}}}}}$

$d$ is the number of features or dimensions of $x$ and $D$ is the Euclidean distance. Choosing a good value for $w$ is critical. However, we can try to find reasonably good values by cross validation.