Course:CPSC522/Learning Markov Logic Network Structure

Learning Markov Logic Network Structure

Principal Author: Jordon Johnson
Papers discussed:
Kok, Stanley, and Pedro Domingos. "Learning the structure of Markov logic networks." Proceedings of the 22nd international conference on Machine learning. ACM, 2005.
Mihalkova, Lilyana, and Raymond J. Mooney. "Bottom-up learning of Markov logic network structure." Proceedings of the 24th international conference on Machine learning. ACM, 2007.

Abstract

This page discusses methods that have been used to learn the structure of Markov Logic Networks (MLN). Some background on Markov Logic Networks is given. A top-down method for learning MLN structure is described; and then a bottom-up approach is discussed that has been shown to offer performance improvements over the top-down method.

Builds on

Markov Logic Networks are a statistical relational model that combines Markov networks and first-order logic.

Content

Terms Used

This page uses the terminology of Mihalkova and Mooney, as follows:

• A term can be a constant, a variable, or a function applied to other terms; ground terms are those with no variables.
• When a predicate is applied to terms, it is called an atom, or positive literal; a negated atom is called a negative literal. A ground literal (or gliteral) is a literal with no variables (i.e. the terms in the literal are all ground terms). Conversely, a vliteral contains only variables.
• A disjunction of literals is called a clause.
  
• Given a domain, assigning truth values to all possible ground literals results in a world.
• The clauses in the MLN are often called its structure.

Markov Logic Networks

Consider a knowledge base (KB) in first-order logic (FOL). Under FOL alone, if a world violates even one of the clauses in the KB, the world is deemed impossible. Thus the viability of a world under a KB is a binary function (a world is either possible or not). Markov logic networks (MLN) allow us to soften this restriction on worlds, so that a world that violates one or more clauses in the KB simply becomes less probable for each clause violated.

A MLN consists of a set of FOL clauses, where each clause is given a weight. The weights are used to determine the probability of a given world, as will be seen.

Consider a KB and some domain $D$. A world can be specified by the set of all possible ground literals, $X$, obtained from the predicates of the KB and the constants of $D$; let $x$ be an assignment of truth values to the elements of $X$. Futher, let $c_{i}$ be some clause in the set of clauses $C$; let $w_{i}$ be the weight associated with $c_{i}$; and let $G_{c_{i}}$ be the set of possible groundings of $c_{i}$. Then the probability of $x$ is

$P(X=x)={1 \over Z}exp\left(\sum _{c_{i}\in C}w_{i}\sum _{g\in G_{c_{i}}}g(x)\right)$

where $Z$ is a normalization constant. The function $g(x)$ only takes the values {1,0}, depending on whether the grounding $g$ of the relevant clause is true or false. In other words, the formula above counts how many groundings of each clause are true. Also of note is that, as the weights increase, so does the effect of violating clauses, to the point where the MLN is equivalent to a KB in the case of all infinite weights. In other words, the weights determine how "forgiving" an MLN is to violations of its clauses. One can learn these weights by maximizing the likelihood of the relevant relational database.

Constructing a Markov Network from a MLN

Figure 1. (a) A simple MLN, consisting of clauses and their corresponding weights. Note that the domains used are people ({brando, coppola}) and movie titles ({godFather}). (b) A Markov network constructed from the MLN in (a). (Source: Mihalkova and Mooney)

A MLN can be thought of as "a template for constructing Markov networks". Mihalkova and Mooney use the simple example shown in Figure 1.

Constructing a Markov network from a MLN is a fairly straightforward process:

• Create a node for each possible grounded literal in the domain. For example, in Figure 1 the predicate Actor(A) can be grounded by instantiating A with brando or coppola; note that a node exists for each of those groundings.
• Create an edge between each pair of nodes if the corresponding grounded literals appear together in a grounding of a clause. For example, in Figure 1 the grounded literals Actor(brando) and Director(brando) appear together in a grounding of the first clause in the MLN, and so there is an edge between those two nodes. Note that the grounded literals that appear together in this way form cliques.

Scenarios for Learning MLN Structure

We may wish to learn the structure of a MLN to accomplish one of two goals:

• to learn the MLN "from scratch" (i.e. all we have is unit clauses)
• to refine (i.e. correct errors in) a KB created manually created by some domain expert

In the case of refining an existing KB, we would want to account for errors such as omitting predicates from clauses (or adding spurious ones), reversing implication direction, or using incorrect logical connectives.

Top-down Structure Learning (Kok and Domingos)

Note: This section is a partial summary of the work of Kok and Domingos. The algorithms and definitions presented here are taken directly from their paper, with little or no modification.

Whether learning a MLN from scratch or refining an existing KB, the first step is to add all the "unit clauses" (consisting of a single predicate) to the MLN, since their weights "capture (roughly speaking) the marginal distributions of the predicates, allowing the longer clauses to focus on modeling predicate dependencies".

Also of note while learning a MLN is that not only are the clauses themselves being learned, but also their weights. L-BFGS, a quasi-Newton optimization algorithm, is used to learn the weights in the paper.

Evaluation Measures

In order to evaluate candidate clauses for inclusion in the MLN, some scoring mechanism is needed. In order to avoid a learning bias toward predicates with high arity values, Kok and Domingos defined (and subsequently used) the weighted pseudo-log-likelihood (WPLL) as follows:

$logP_{w}^{*}(X=x)=\sum _{r\in R}c_{r}\sum _{k=1}^{g_{r}}logP_{w}(X_{r,k}=x_{r,k}|MB_{x}(X_{r,k}))$

where

• $R$ is the set of predicates
• $g_{r}$ is the number of groundings of predicate $r$
• $x_{r,k}$ is the binary truth value of the kth grounding of $r$
• $MB_{x}(X_{r,k})$ is the state of the Markov blanket of the kth grounding of $r$
• $c_{r}$, the predicate weight, is chosen depending on user goals (for the paper it was set to $1/g_{r}$)

Clause Construction Operators

The following operators are used to construct or modify candidate operators:

• add a literal
• remove a literal (only from hand-coded clauses or their descendants)
• flip a predicate's sign

For example, suppose a sleep-deprived expert was working with the dataset from the example in Figure 1 and mistakenly hand-coded the clause

$Actor(B)\land Movie(T,A)\land \neg WorkedFor(A,B)\rightarrow Movie(T,B)$

If we first remove a literal

$Movie(T,A)\land \neg WorkedFor(A,B)\rightarrow Movie(T,B)$

and then flip a sign

$Movie(T,A)\land WorkedFor(A,B)\rightarrow Movie(T,B)$

we see that we obtain the third clause in Figure 1.

Search Strategies

Two search strategies were implemented: one faster (based on beam search), and one more complete (called shortest-first search). Only the beam-search method is described here, since it is the method used in the comparison with Mihalkova and Mooney's bottom-up approach.

The beam search strategy starts from unit and hand-coded clauses and does the following:

1. applies the operators to generate candidate clauses
2. evaluates the candidates using WPLL, stores the best clause so far, and keeps the best b clauses for the next iteration
3. repeats 1 and 2 until none of the candidates improve over the stored best clause
4. adds the best clause to the MLN

A more detailed version of the approach is given in the paper as pseudocode:

   function FindBestClauses(R, MLN, Score, Clauses0, DB)
   inputs: R, a set of predicates
       MLN, a clausal Markov logic network
       Score, WPLL of MLN
       Clauses0, a set of clauses
       DB, a relational database
   output: BestClause, a clause to be added to MLN
   BestClause ← ∅
   BestGain ← 0
   Beam ← Clauses0
   Save the weights of the clauses in MLN
   repeat
       Candidates ← CreateCandidateClauses(Beam, R)
       for each clause c ∈ Candidates
           Add c to MLN
           LearnWeights(MLN, DB)
           Gain(c) ← WPLL(MLN, DB) − Score
           Remove c from MLN
           Restore the weights of the clauses in MLN
       Beam ← {The b clauses c ∈ Candidates with highest
       Gain(c) > 0 and with Weight(c) > ∈ > 0 }
       if Gain(Best clause c∗ in Beam) > BestGain
           BestClause ← c∗
           BestGain ← Gain(c∗
       )
   until Beam = ∅ or BestGain has not changed in two iterations
   return {BestClause}

Bottom-up Structure Learning (Mihalkova and Mooney)

Note: This section is a partial summary of the work of Mihalkova and Mooney. The algorithms and definitions presented here are taken directly from their paper, with little or no modification. The contribution of this paper is in the reduction of the search space, described below, that results in performance improvements over the beam-search approach described in the previous section.

Figure 2. A Markov network template. (Source: Mihalkova and Mooney)

It can be seen that the Markov network generated in Figure 1 is made up of multiple copies of the Markov network template shown in Figure 2 (one for each grounding of the predicates). A bottom-up approach to learning MLN structure is then to first automatically create such a template from the available data. The nodes in the template, called "template nodes" or TNodes, are then used as the components from which clauses can be created. The skeleton of the bottom-up approach is as follows:

   for each P in Preds do    // P is a predicate; Preds is the set of all predicates
       construct TNodes for P    // see TNode Construction
       connect TNodes to form a Markov network template    // see Adding the Edges
       create candidate clauses using the template to constrain the search    // see Search for Clauses
   end for
   remove duplicate clauses
   evaluate clauses and add the best ones to the MLN

Recall that, in the Markov network generated from a MLN, the literals involved in the grounding of a clause form a clique; thus the search space for MLN structure can be restricted to only those clauses corresponding to cliques in the template. Once a Markov network template is created, the set of all possible clauses from each maximal clique is generated, and the clauses are evaluated using the WPLL score.

TNode Construction

Mihalkova and Mooney summarize the construction of TNodes as follows:

TNodes contain conjunctions of one or more vliterals and serve as building blocks for creating clauses. Intuitively, TNodes are constructed by looking for groups of constant-sharing gliterals that are true in the data and variablizing them [(i.e. replacing their constants with variables)]. Thus, TNodes could also be viewed as portions of clauses that have true groundings in the data ... The result of running TNode construction for [a predicate] P is the set of TNodes and a matrix MP containing a column for each of the created TNodes and a row for each gliteral of P. Each entry MP[r][c] is a Boolean value that indicates whether the data contains a true grounding of the TNode corresponding to column c with at least one of the constants of the gliteral corresponding to row r. This matrix is used later to find the edges between the TNodes.

The following two definitions are used:

• Definition 1: Two literals are connected if there exists a constant or variable that is an argument of both.
• Definition 2: A chain of literals of length $l$ is a list of $l$ literals such that for $1<k\leq l$ the kth literal is connected to the (k − 1)th via a previously unshared variable.

Pseudocode for the construction of a set of TNodes and its corresponding matrix:

   Input:
       P: Predicate currently under consideration
       m: Maximum number of vliterals in a TNode
   Output:
       TNodeVector: Vector of constructed TNodes
       MP: Matrix of Boolean values
   Procedure:
       Make head TNode, headTN, and place it in position 0 of TNodeVector
       for each (true or false) ground literal, GP, of P do
           Add a row of 0-s to MP
           if GP is true then
               Set MP[lastRow(MP)][0] = 1
           end if
           Let CGP be the set of true ground literals connected to GP
           for each c ∈ CGP do
               for each possible TNode based on c do
                   newTNode = CreateTNode(c, GP, headTN, m)
                   position = TNodeVector.find(newTNode)
                   if position is not valid then
                       append newTNode to end of TNodeVector
                       append a column of 0-s to MP
                       position = numColumns(MP) − 1
                   end if
                   Set MP[lastRow(MP)][position] = 1
               end for
           end for
       end for

Pseudocode for the creation of an individual TNode:

   Input:
       GP: Current gliteral of P under consideration
       c: Gliteral connected to GP on which TNode is based
       headTN: Head TNode
       m: Max number of of vliterals allowed in a TNode
   Output:
       newTNode: The constructed TNode
   Procedure:
       size = pick a size for this TNode (between 1 and m)
       v = variablize(c)
       Create newTNode containing v
       prevGliteral, lastVliteralInChain = c, v
       while length(newTNode) < size do
           c1 = pick true gliteral connected to prevGliteral
           v1 = variablize(c1) and add v1 to newTNode
           prevGliteral, lastVliteralInChain = c1, v1
       end while

Adding the Edges

Since the templates being created are essentially Markov networks (except with vliterals instead of gliterals), finding the edges of the templates is essentially a Markov network structure learning problem, for which the matrix MP can be used as training data, and for which a number of suitable learning algorithms already exist. The algorithm chosen for the paper was the Grow-Shrink Markov Network (GSMN) algorithm, which infers structure using statistical independence tests.

Search for Clauses

As mentioned earlier, clauses are only constructed from TNodes forming cliques in the Markov network templates. Additional restrictions are imposed to further reduce the search space:

• The head TNode (from the algorithm for constructing a set of TNodes) must be a part of the clique.
• At most one multiple-literal TNode and one TNode containing a single literal of arity > 1 may be in a clause.

Given these restrictions, all possible clauses with lengths from 1 to the size of the clique are generated; then duplicates are discarded, and the remainder are scored using WPLL. In order to obtain the weight for each clause, L-BFGS is used as with the top-down approach. Only clauses that increase the overall WPLL of the learned MLN are retained.

Comparison to Top-down Approach

Figure 3. Performance comparison of bottom-up (BUSL) and top-down (TDSL) methods on three knowledge bases. (Source: Mihalkova and Mooney)

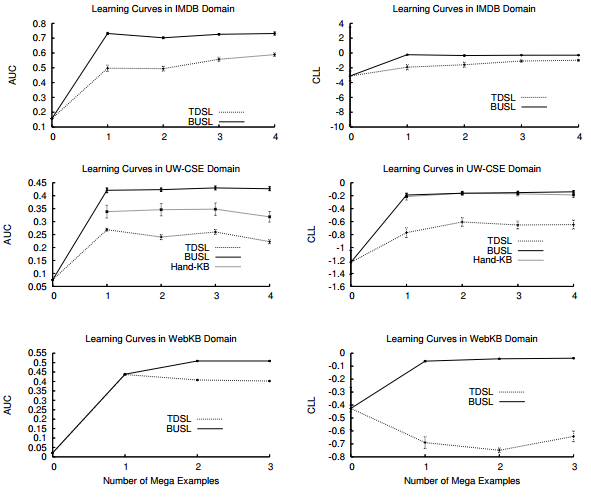
The bottom-up approach of Mihalkova and Mooney (BUSL) was compared to the beam-search method of Kok and Domingos (TDSL) using three relational databases: IMDB (movies), UW-CSE (people in a Computer Science department), and WebKB (information related to four universities). Each database was broken down into connected sets of facts, or "mega-examples".

Figure 4. Performance comparison of bottom-up (BUSL) and top-down (TDSL) methods on three knowledge bases, with respect to runtime. (Source: Mihalkova and Mooney)

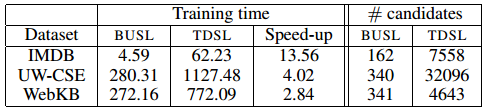
The performance of the two methods on these datasets was measured using two metrics: the area under the precision-recall curve (AUC) and the conditional log-likelihood (CLL). The results of the comparison are shown in Figure 3. BUSL performs better than TDSL in all but one case under the AUC metric, and it outperforms TDSL in all cases under CLL. Figure 4 shows the training times, speedup factors, and average number of clauses considered by each method for the three databases; as is shown, the refined search space of BUSL results in considerable improvement.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.