Course:CPSC522/Hyperspherical Variational Auto-Encoders

Hyperspherical Variational Auto-Encoders

Variational auto-encoders for data with a hyperspherical latent structure and an application to real world data.

Paper 1: Hyperspherical Variational Auto-Encoders

Paper 2: Deep Generative Model Embedding of Single Cell RNA-Seq Profiles on Hyperspheres and Hyperbolic Spaces

Principal Author: Sarah Chen
Collaborators:

Abstract

Variational Auto-Encoders (VAE) are one of the most widely used forms of unsupervised learning today. They are useful since they can be used for dimensionality reduction and as a generative model, VAEs can also generate new samples. However, the use of a normal distribution for the prior and posterior, while mathematically convenient, may fail for data that has a latent hyperspherical structure. This article discusses two papers, one that proposes the use of the von Mises-Fisher (vMF) distribution and another that uses the proposed hyperspherical VAE for single-cell RNA sequencing data.

Builds on

This page builds on Variational Inference, and Variational Auto-Encoders.

Related Pages

Related to VAEs are Generative Adversarial Networks which are also generative models.

Background

Background knowledge of probability, particularly the basics of the normal distribution and rejection sampling are assumed. Reading Variational Auto-Encoders is highly recommended but some basic information will be given.

Notation

VAEs that use the normal distribution will be denoted by ${\mathcal {N}}$-VAE and VAEs that use the von-Mises Fisher (vMF) distribution will be denoted by ${\mathcal {S}}$-VAE.

Variational Auto-Encoders

This is a very brief reiteration of the objective function for VAEs, since it is the primary difference of ${\mathcal {S}}$-VAEs from ${\mathcal {N}}$-VAEs. A variational auto-encoder (VAE) aims to maximize the marginal log-likelihood of the data but as this computation is intractable, it maximizes a lower bound instead known as the evidence lower bound (ELBO).

$$ELBO=\mathbb {E} _{q(z|x;\phi )}[{\textbf {log}}(p(x|z;\theta )]-\mathbb {KL} (q({\textbf {z}}|{\textbf {x}};\phi )||p({\textbf {z}}))$$

A VAE has two parts, the encoder and the decoder. An input $\mathbf {x}$ is mapped to a lower dimensional representation $\mathbf {z}$ by the encoder. The decoder then maps $\mathbf {z}$ to $\mathbf {\hat {x}}$ where the aim is that $\mathbf {x}$ and $\mathbf {\hat {x}}$ are as similar as possible. This leads to the two distributions $q(z|x;\phi )$ and $p(x|z;\theta )$ in the ELBO, and the VAE tries to learn the parameters $\phi$ and $\theta$ to maximize the ELBO. $p(\mathbf {z} )$ in the ELBO is the prior.

Paper 1: Hyperspherical Variational Auto-Encoders

Sphere Geometry

When we think of a sphere, we generally think of a 3D object. However, this can be generalized to lower and higher dimensions. In 2 dimensions, a sphere is a circle, specifically the 2-sphere. In 3 dimensions we have what we usually think of as a sphere, the 3-sphere. For dimensions $\geq 4$, we generalize the definition of a sphere. An n-sphere is defined as $S^{n}:=\{x\in \mathbb {R} ^{n+1}\mid ||x||_{2}=1\}$.
More generally $S^{n}:=\{x\in \mathbb {R} ^{n+1}\mid ||x||_{2}={\frac {1}{K}}\}$, $K>0$ where $K$ is a measure of the curvature. When $K$ is small, the curvature is small resulting in a very large sphere and when on the sphere, the curve looks flat such as the Earth. The opposite occurs when $K$ is large.

von Mises-Fisher Distribution

The von Mises-Fisher (vMF) distribution is a generalization of the normal distribution on a hypersphere. For a random unit vector, $\mathbf {z} \in \mathbb {R} ^{m}$ or $\mathbf {z} \in S^{m-1}$, its PDF is

$$q(\mathbf {z} |\mu ,\kappa )=C_{m}(\kappa )\exp {(\kappa \mu ^{T}\mathbf {z} )}$$

As can be seen from the PDF, there are two parameters $\mu \in \mathbb {R} ^{m}$ which is the mean direction and $\kappa \in \mathbb {R} _{\geq 0}$ which is the concentration parameter. The concentration parameter indicates how much $\mathbf {z}$ is concentrated around $\mu$ with higher values indicating a higher concentration.
$C_{m}$ is a normalization constant. The equation for it is below. It is hard to compute and has no closed form. $I_{\nu }(.)$ is the modified Bessel function of the first kind, where $\nu$ indicates the order.

$$C_{m}(\kappa )={\frac {\kappa ^{m/2-1}}{(2\pi )^{m/2}I_{m/2-1}(\kappa )}}$$

When the concentration parameter is 0, the vMF distribution becomes a uniform distribution on the hypersphere, $U(S^{m-1})$.

The Problem

Spherical representations have been shown to better capture directional data such as protein structure and wind direction. Some data may also be normalized to focus on the direction giving it a spherical nature such as an image of a digit being rotated. VAEs using a normal distribution fail to learn this spherical latent structure. This is because in low dimensions, a normal distribution encourages points to be in the center causing collapse of the spherical structure. For example, consider a $S^{1}$ sphere (a circle) mapped to $\mathbb {R} ^{2}$, the KL-divergence will encourage the posterior to follow a normal distribution causing the cluster centers to gather around the origin. Accordingly, when the effect of the KL divergence is decreased, it gets better.
As a result, the use of the vMF distribution is proposed. Assume the latent representation has dimension $m$. For the posterior, we use $vMF(\mu ,\kappa )$. For the prior, we use the uniform distribution on a hypersphere, $U(S^{m-1})$. In addition, while in high dimensions, the normal distribution is known to resemble a uniform distribution on the surface of a hypersphere, it may be the case that a uniform distribution naturally defined to be on the hypersphere, $U(S^{m-1})$ performs better.

The Objective Function

The objective function we wish to maximize for a VAE is

$${\mathcal {L}}(\phi ,\theta )=\mathbb {E} _{q(z|x;\phi )}[{\textbf {log}}(p(x|z;\theta )]-\mathbb {KL} (q({\textbf {z}}|{\textbf {x}};\phi )||p({\textbf {z}}))$$

Due to the use of a vMF distribution, the objective function is affected.

KL Divergence

Substituting in the vMF posterior and vMF prior, we obtain

$$\mathbb {KL} (vMF(\mu ,\kappa )||U(S^{m-1}))=\kappa {\frac {I_{m/2}(\kappa )}{I_{m/2-1}(\kappa )}}+\log {(C_{m}(\kappa )}-\log {({\frac {2(\pi ^{m/2})}{\Gamma (m/2)}})}^{-1}$$

Due to the Bessel function, we cannot use automatic differentiation. Instead, the gradient must be computed manually. As $\mu$ is not present, the KL divergence does not affect $\mu$ and we only compute the gradient with respect to $\kappa$. Previous work has been done using a VAE with a vMF distribution, but the concentration parameter, $\kappa$, was not learned.

Reconstruction Term

As seen in Variational Auto-Encoders, the reconstruction term $\mathbb {E} _{q(z|x;\phi )}[{\text{log}}p(x|z;\theta )]$ requires that we sample from $q(z|x;\phi )$, but this raises the issue of backpropagation. This was resolved by using the reparameterization trick where we sample $\epsilon \sim s(\epsilon )$ and $z=h(\epsilon ,\phi ,x)$. Similarly, for the ${\mathcal {S}}$-VAE, we sample $\epsilon \sim s(\epsilon )$, and reparameterize $z=h(\epsilon ,\phi ,x)$ but unlike the normal distribution, sampling from the vMF distribution requires rejection sampling. The process for rejection sampling is described in the next section. Fortunately, we can still use the reparameterization trick if the proposal distribution can be reparameterized. Dropping the $x$ from $h(\epsilon ,\phi ,x)$ to make things simpler, we have the approximate posterior distribution, $q(h(\epsilon ,\phi );\phi )$ and the proposal distribution, $r(h(\epsilon ,\phi );\phi )$. The accepted samples have distribution, $\pi (\epsilon ;\phi )=s(\epsilon ){\frac {q(h(\epsilon ,\phi );\phi )}{r(h(\epsilon ,\phi );\phi )}}$. Using this, we obtain the reconstruction term, $\mathbb {E} _{\pi (\epsilon ;\phi )}[f(x|h(\epsilon ,\phi );\theta )]$. We can then proceed to take the gradient which requires the log derivative trick and use stochastic gradient descent to train the ${\mathcal {S}}$-VAE.
The vMF distribution however does require an additional reparameterization. After we accept or reject the transformed sample $h(\epsilon ,\phi )$, we sample another random variable $v\sim \pi _{2}(v)$. This is transformed to be $z={\mathcal {T}}(h(\epsilon ,\phi ),v;\phi )$ where $z\sim q(z|x;\phi )$, our approximate posterior. Taking the gradient proceeds much the same way it did before.

Rejection Sampling

A very high level overview of rejection sampling from a vMF distribution is given. Assume we want to sample from $vMF(\mu ,\kappa )$ and the latent space has dimension $M$. A theorem holds that an $M$-dimensional vector $z=({\sqrt {1-\omega ^{2}}}\mathbf {v} ^{T},\omega )^{T}\sim vMF((0,...,1)^{T},\kappa )$, where $\omega \sim g(\omega ,\kappa )$, $\mathbf {v}$ is a vector uniformly distributed in ${\mathcal {S}}^{M-2}$, and $(0,...,1)^{T}\in \mathbb {S} ^{M-1}$. $(0,...,1)^{T}$ is a unit vector so $...$ is all 0s.We thus sample $\omega$ using rejection sampling. As $\omega$ is 1-dimensional, rejection sampling is still efficient and does not suffer from the curse of dimensionality as $M$ grows large. We use the proposal distribution $r(\omega ,\kappa )$.
To sample from the proposal distribution, we sample $\epsilon \sim Beta$ and transform $\epsilon$ using the function $h(\epsilon ;\kappa )$ to obtain $\omega =h(\epsilon ;\kappa )$. It can be proved that this generates samples such that $\omega \sim r(\omega ,\kappa )$. After, we accept or reject $\omega$ using $u\sim U[0,1]$. If $\omega$ is accepted, a vector $\mathbf {v}$ is sampled from $U(S^{m-2})$. $\omega$ and $\mathbf {v}$ are transformed using ${\mathcal {T}}(\omega ,{\bf {{v})}}$ to obtain $z'=({\sqrt {1-\omega ^{2}}}\mathbf {v} ^{T},\omega )^{T}$. As mentioned earlier, $z'\sim vMF((0,...,1)^{T},\kappa )$ but we want $z\sim vMF(\mu ,\kappa )$. To do this, we use the Householder reflection to transform $z'$ and obtain $z\sim vMF(\mu ,\kappa )$.

The proof that these reparameterizations hold and many other important derivations have been largely omitted. Likewise, details for rejection sampling have not been included such as the equation for the proposal distribution. It is highly recommended to consult the paper for them.

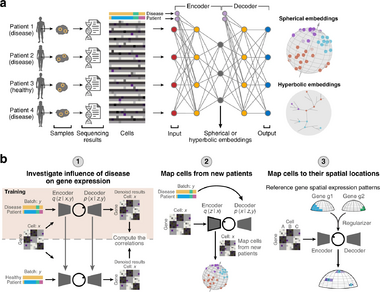
Paper 2: Deep generative model embedding of single-cell RNA-Seq profiles on hyperspheres and hyperbolic spaces

The Problem

Single-cell RNA sequencing (scRNA-seq) data is crucial to gaining insights into biological systems such as identifying new cell types, their differentiation trajectories, and spatial positions. The dimensionality of the observed data is very high though whereas the data intrinsically lies on a lower dimension since much of the variance can be explained by a few factors. Dimensionality reduction then is a key step in performing further downstream analyses and VAEs have been used to do so. However, ${\mathcal {N}}$-VAEs can suffer from poor performance as they encourage different cell types to cluster in the center. Thus, the use of a ${\mathcal {S}}$-VAE is proposed instead. In addition, normally VAEs have only been applied to handle one batch effect. In this paper, it is extended to handle multiple batch effects, which is especially important for scRNA-seq data which can have technical and biological batch effects.

The ${\mathcal {S}}$-VAE for scRNA-seq Data

The input to a ${\mathcal {S}}$-VAE when using scRNA-seq data is a dataset ${\mathcal {D}}=\{(\mathbf {x} _{i},\mathbf {y} _{i})\}_{i=1}^{N}$, where $D$ is the number of genes. $\mathbf {x} _{i}$ is a vector that contains the count of each gene in cell $i$. $\mathbf {x} _{i}$ is log-transformed and then scaled to have a unit $\ell ^{2}$ norm. To account for batch effects, $y_{i}$ is a categorical vector that indicates the batch of $x_{i}$. The VAE now takes in two inputs $x_{i}$ and $y_{i}$. With the addition of $y_{i}$, the joint distribution becomes

$$p(\mathbf {x} _{i},\mathbf {y} _{i},\mathbf {z} _{i}|\mathbf {\theta } _{i})=p(\mathbf {y} _{i}|\mathbf {\theta } _{i})p(\mathbf {z} _{i}|\mathbf {\theta } _{i})p(\mathbf {x} _{i}|\mathbf {y} _{i},\mathbf {z} _{i},\mathbf {\theta } _{i})$$

Note that $\mathbf {\theta } _{i}$ are the parameters of different distributions and is only used for simplicity. $p(\mathbf {y} _{i}|\mathbf {\theta } _{i})$ is the categorical distribution. $p(\mathbf {z} _{i}|\mathbf {\theta } _{i})$ the prior is still a uniform vMF distribution and the posterior is still a VMF distribution which is approximated by $q(\mathbf {z} _{i}|\mathbf {y} _{i},\mathbf {x} _{i},\mathbf {\phi } )$ where the parameters come from the neural network. $p(\mathbf {x} _{i}|\mathbf {y} _{i},\mathbf {z} _{i},\mathbf {\theta } _{i})$ is assumed to follow a negative binomial distribution from previous work.

An overview of sPhere and its applications. a. scRNA-seq data is input to the VAE from which spherical embeddings are obtained. b. The VAE can be used to investigate how genes affect disease, map new cells, and infer spatial location. Taken from https://www.nature.com/articles/s41467-021-22851-4%7C#citeas.

The Objective Function

The objective function remains the same except for the addition of a penalty term to help stabilize training. $\mathbf {x} _{i}$ is downsampled so that only 80% of the UMI counts are retained. The downsampled $\mathbf {x} _{i}$ is represented by $\mathbf {\hat {x}} _{i}$ which have latent representations $\mathbf {z} _{i}$ and $\mathbf {\hat {z}} _{i}$. The penalty term is $-\sum _{j=1}^{M}(\mathbf {z} _{i,j}-\mathbf {\hat {z}} _{i,j})^{2}$ as we want $\mathbf {z} _{i}$ and $\mathbf {\hat {z}} _{i}$to be as close as possible.

Experiments

The ${\mathcal {S}}$-VAE used in this paper was developed as a part of scPhere. A ${\mathcal {S}}$-VAE is demonstrated to have many applications particularly regarding scRNA-seq data. Four experiments are focused on, as the first three evaluate the spherical embeddings and the fourth shows how the ${\mathcal {S}}$-VAE can now be used to correct for multiple batch effects.

Visualization

Six datasets, small and large, were used to evaluate the use of the ${\mathcal {S}}$-VAE for visualization. It was compared against Euclidean embeddings and three other common visualization methods, UMAP, t-SNE, and PHATE. For the small datasets, the Euclidean embeddings experience the problem of cell types clustering around the origin. The rest of the methods performed similarly well. The advantages of the ${\mathcal {S}}$-VAE were seen most clearly with the large datasets as it was able to preserve the global hierarchy of subtypes being close together while in other visualization methods, they were not.

Visualization of a. embeddings obtained from a hyperspherical VAE, b. embeddings from a normal VAE in 2D, and c. embeddings from a normal VAE in 3D. Taken from https://www.nature.com/articles/s41467-021-22851-4%7C#citeas. Adapted from Supplementary Figure 1.

ScPhere Preserves Structure Even in a Low-Dimensional Space

A ${\mathcal {S}}$-VAE and ${\mathcal {N}}$-VAE were trained on a dataset composed of multiple patients with one patient held out for testing. The spherical embeddings were compared against the Euclidean embeddings and also against t-SNE, UMAP, and PHATE with 20 or 50 batch-corrected principal components. K-nearest neighbors was then run and the classification accuracy measured. The spherical embeddings easily outperformed the Euclidean embeddings. Also, interestingly, only a 5D latent space for the spherical embeddings was required to perform better than t-SNE, UMAP, and PHATE with a 50D latent space.

The k-NN classification accuracies for different cell types of one test patient on the y-axis and k=5, k=11, k=17, and k=23, where k is the number of neighbors, on the x-axis. Taken from https://www.nature.com/articles/s41467-021-22851-4%7C#citeas. Adapted from Supplementary Figure 8.

Clustering Cells

As clustering is an important downstream analysis task for scRNA-seq data, the effects of embeddings cells on the surface of a 5D hypersphere and then clustering was examined. The clustering results using the spherical embeddings were found to be very similar to the original clusters, except some cells were grouped into other clusters due to their molecular similarity. It was also found that as batch effects were corrected for, cells originally separated by a batch effect began to merge together. Some clusters of rare cell types were also present even in the low-dimensional latent space.

Batch Effect Correction

A single dataset was used to observe batch effect correction. This dataset had many cells and many batch effects. For example, samples were taken from healthy patients and patients with ulcerative colitis, from different tissues, and at different times. The performance of correcting for the batch effect patient was compared against three other common batch correction methods. scPhere had higher classification accuracies for the different cell types. Multilevel batch correction was also performed and the cells were found to be successfully integrated. This could be seen when using patient and disease status as the batch vector, inflammatory and healthy cells of the same type were mixed together.

Each of these applications of a ${\mathcal {S}}$-VAE to scRNA-seq data have been very briefly summarized. The full details and analysis as well as other applications and useful figures are provided in the paper.

Conclusion

The ${\mathcal {S}}$-VAE is useful for handling data with a hyperspherical latent structure as demonstrated with scRNA-seq data. Despite the data being uniformly concentrated on the hypersphere though, the concentration parameter, $\kappa$ is still fixed. It might be better if it were not. The vMF distribution can also be hard to work with. Further work has been done regarding these issues, specifically in Increasing Expressivity of a Hyperspherical VAE and The Power Spherical distribution. Data can also have a different latent structure than hyperspherical which is why another VAE was used in Deep generative model embedding of single-cell RNA Seq profiles on hyperspheres and hyperbolic spaces for data with a hierarchical structure, so it is important to consider whether a ${\mathcal {S}}$-VAE can be applied to your data.

Annotated Bibliography

Put your annotated bibliography here. Add links where appropriate.

[1] Kingma, D. P. & Welling, M. Auto-encoding variational Bayes. in International Conference on Learning Representations (ICLR, 2014)

[2] Weisstein, Eric W. "Hypersphere." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/Hypersphere.html

[3] Davidson, Tim R., Falorsi, Luca, Cao, Nicola De, Kipf, Thomas, and Tomczak, Jakub M. Hyperspherical variational auto-encoders. In Globerson, Amir and Silva, Ricardo (eds.), Proceedings of the Thirty-Fourth Conference on Uncertainty in Artificial Intelligence, UAI 2018, Monterey, California, USA, August 6-10, 2018, pp. 856–865. AUAI Press, 2018. http://auai.org/uai2018/proceedings/papers/309.pdf

[4] Ding, J., Regev, A. Deep generative model embedding of single-cell RNA-Seq profiles on hyperspheres and hyperbolic spaces. Nat Commun 12, 2554 (2021). https://doi.org/10.1038/s41467-021-22851-4

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.