Buoyancy, Pressure, Bernoulli's Equation
| This article is part of the PhysicsHelp Tutoring Wiki |
Buoyancy
Back to: PhysicsHelp
The buoyant force tends is a force that acts in the upward direction when an object is partially or fully submerged in water.
The equation for the force is:
is the buoyant force, pointing upwards, in Newtons ().
is the volume submerged in metres cubed ().
is the density of the liquid (or gas) that the object is being submerged in kilograms per metre cubed ().
is the force of gravity in Newtons per kilogram ().
Note: if an object is only partially submerged, then is only the volume of the submerged section.
Consider a floating object. The floating object has two forces acting on it, that of gravity and that of buoyancy. If the object is not sinking or rising, then these two forces will be equal. The force of gravity generally the form:
is the force of gravity in Newtons ().
is the mass in ().
is the acceleration due to gravity in Newtons per kilogram ().
is the density of the object in kilograms per metre cubed ().
is the volume of the object in metres cubed ().
This equation will be equal to the above one in static equilibrium, and depending what variables are given, you can use these to solve for the remaining ones.
Problem Solving
The key to solving these problems is to equate the mass of the object and the water being displaced. For example:
Q: A -tall cylinder floats in water with its axis perpendicular to the surface. The length of the cylinder above water is 2.00cm . What is the cylinder's mass density?
A: The volume of water displaced is the volume of cylinder in the water:
The density of water is , so we have mass of water displaced:
We know that the mass of the object equals the mass of the water displaced, so we solve for the density:
Pressure
Pressure is a force per unit area. Thus, the force on an object is the pressure applied times the area over which it is applied:
is the total force in Newtons (). is the pressure in Pascals (). is the area in metre squared ().
So if we imagine the window of a submarine, the pressure inside is (or ) and the pressure outside could be . The pressure difference times the area of the window () would give the total force from the water on the submarine window.
We can also calculate the pressure at some depth. For this we use the equation:
is the pressure at height in Pascals (). is the pressure at height in Pascals (). is the density of the liquid, in kilograms per metre cubed (). is the force of gravity, in Newtons per kilogram (). is the height for the pressure in meters (). is the height for the pressure in meters ().
Problem Solving
The key to solving hydraulic lift problems is to remember that the pressure at equal heights of an incompressible fluid is equal.
Problem 1
Q: Consider a physics student standing on an oil-filled hydraulic lift to hold up four football players at the same height. If the physics student's piston is in diameter, what is the diameter of the football players' piston?
A: We know the pressure at equal heights in the fluid must be equal. We can calculate the pressure on the football side:
On the physics student's side, we have:
By equating these two pressures we can solve for the radius of the piston on the football players' side:
Thus the diameter of the football players' piston is:
Problem 2
Q: A physics student balances a elephant using a hydraulic lift filled with oil (). (a): The elephant's piston is in radius, what is the radius of the students piston? (b): If a second physics student joins the first, how high will they lift the elephant?
A(a): Again we can equate the pressure on both sides to find the radius of the student's piston:
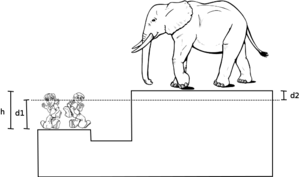
A(b): When the second student gets on the lift, the system is no longer in equilibrium and will move. The students' piston will move down and the elephant's piston will move up. When the lift has finished moving, the elephant will be some height above the students. The important concept to realize here is that there are three different distanced to consider in this problem: The total height difference between the students and the elephant, the distance moved by the students, and the distance moved by the elephant. The two sides won't move the same distance because their pistons are different sizes.
In this new configuration, we still know that the pressure of the fluid at the same height is equal, so we can consider the pressure at the height of the students and compare it to the pressure at the same height on the elephant side. But the pressure on the elephant's side is not just the pressure due to the mass of the elephant, but also the pressure due to the mass of the oil above that height. We know that the mass of the oil is and the volume of oil can be written , where h is the total height difference and A_2 is the area of the elephant's piston, so we can write the total force of gravity from the oil above the piston as:
Then the total force at that height on the elephant's piston is the sum of the force due to gravity of the elephant and the oil:
The total pressure at that point is simply the force divided by the area of the piston:
Clearly the 's in the second term cancel and we're left with:
Where is the pressure just due to the mass of the elephant. We can now set this equal to , the pressure due to the students, and solve for . We have:
But remember that we're not quite done: we know the elephant's total height above the students, but because the students side dropped a bit we still need to work out how high the elephant was lifted about its initial height. To do this we must make two crucial observations. First, we must realize that clearly the sum of the distance moved by the students' side and the elephants side must equal the total difference in height , since they started off at the same height. Thus:
Where is the distance moved by the students' side and is the distance moved by the elephant's side. Secondly we know that the total volume of oil displaced on each side must be equal, otherwise the system would have gained or lost oil. But we know that the volume displaced is just the distance moved times the area, so we have:
If we solve one of these equations for and substitute into the other, we can solve for to get:
Then we can plug in our numbers to get a value for :
Thus the elephant was lifted .
One strategy for these types of problems is to simple memorize the most relevant formulas, and , but notice how the whole solution of the problem was based solely on the idea that pressure at equal heights of an incompressible fluid is equal. If you remember this fact, you should be able to use simple reasoning and algebra to adapt to many kinds of problems without memorizing which formulas to use.
Another method for finding the height the elephant is raised (by re-factoring the problem)
If you understand the reasoning behind this method, it will make some of the hardest problems hydraulics problems in this course trivial to solve. However if you do not entirely understand it, it is best not to use this method because you are less likely to be awarded partial marks if you use it incorrectly.
Now consider what would happen if instead of a hydraulic system, this were an open u-tube filled with the same fluid. If we were then to pour an additional 70 kg of the fluid into the left opening, the fluid would tend to be distributed such that the level on both sides of the u-tube would be equal in height from the ground.
Now if we need to calculate how much the fluid level increases on the right side, we simply have to:
a) calculate the volume of 70 kg of the fluid
b) calculate the height of this volume of fluid for the total cross section area on both sides of the u-tube
a)
b)
We know that if fluid were poured into either end of the u-tube, the fluid level will change and finally come to an equilibrium so that it is the same on both sides. Calculate the fluid level rise is possible since the u-tubes are assumed to have uniform cross sections.
So, the area upon which the volume of fluid is distributed is given by:
Then to calculate the height increase in the level of the fluid:
Explanation for why this produces the same answer.
In the case of a u-tube where fluid is added to one end, imagine that the fluid does not mix up or get dispersed in the rest of the fluid. Instead imagine a cylinder of the newly added fluid pushing down on the left side. Since the added fluid is of the same properties as the fluid that was originally in the u-tube, we know that to calculate the height increase we need only to know the volume of the fluid and the radii of the two ends of the u-tube.
Now imagine, if, instead of adding fluid to one end of a u-tube, we have a hydraulic system with an additional mass added to one end. Just like in the first case where the imaginary fluid remains on top, we have an additional mass to account for. Since the effect is the same for a weight exerting a force on a certain fluid area, the calculations done for the u-tube must also be valid in this case.
Bernoulli's Equation
Bernoulli's Equation relates the pressure of a fluid with its height and velocity, allowing you to predict the properties as a fluid at a general point in a complicated system pipes based on your knowledge of it a some particular point. The full equation takes the following form:
is the velocity of the fluid in metres per second ()
is the gravitational constant in metres per second squared ()
is the height of the fluid in meteres ()
is the pressure of the fluid in Pascals ()
is the density of the liquid in kilograms per metre cubed ()
is a constant.
Another useful fact to remember related to bernoulli's equation is the fact that in a steady flow of an incompressible liquid, the total rate of volume flow per unit time at any point is constant. This is easy to understand because it is basically a statement that since the liquid is incompressible, it can't "bunch up" or "spread out" at any point (the density of the liquid is constant). This means that if you have liquid flowing through a pipe with a shrinking diameter, the velocity of the liquid much increase: Consider that after a small time a small bunch of liquid travels a distance , where is the velocity. Then the total volume that has been displaced is , where A is the area of the pipe at this point. In other words: , and thus we say:
Problem Solving
Q: A horizontal circular pipe 10.0 cm in diameter has a smooth reduction in diameter to a pipe 5.00 cm in diameter but remains at a constant height. If the pressure of the water in the larger pipe is 8.00 x 10^4 Pa and the pressure in the smaller pipe is 6.00 x 10^4 Pa, at what rate does water flow through the pipe?
A: Using Bernoulli's equation, we can say:
Where we have cancelled the terms since the height is constant.
Next we can say that since the volume flow rate is constant:
Plugging this into the previous line give us:
Which we can solve for
Plugging in the numbers from the question gives us:
Now, we want to find the flow rate of the water, so which is just the area times the velocity at some point in the flow. So we've solve for the velocity in the smaller pipe, so we can calculate the flow rate using the area of the smaller pipe:
- Back to PhysicsHelp