Alpha Function in Q-Learning

Alpha Function in Q-Learning

We will investigate different alpha functions and check if they converge in theory and practice.

Principal Author: Fardad Homafar

Collaborators:

Abstract

We will start with Q-learning. It is important to know what is the motivation behind implementing this agent on our reinforcement learning problems. Then, we will investigate some alpha functions as a game-changing factor in this field. First, we will check if they converge in theory. After that, to practically test them, we will implement them in a Markov Decision Process (MDP) problem. Finally, we will discuss why or why not they are not converging.

Builds on

We will implement Q-learning agent on our reinforcement-learning problem. Reinforcement-learning is a subset of machine learning methods in which an agent learns by interacting with an environment instead of a model that tries to find patterns in a dataset (supervised learning). To test our proposed alpha functions in practice, we implement them on a MDP problem. Markov Decision Process(MDP) is a mathematical framework for modeling decision making; mostly when the agent needs to go beyond a set of fixed decisions or where the outcomes are partly random and it is not clear how long the agent has to keep going. To do so, AIpython package was used.

Related Pages

Reinforcement learning is the branch to which Q-learning agents belong. To do some convergence tests in theory we need to use Ermakoff's test. AIpython package eases our procedures.

Content

Q-Learning

Q-learning, originally an incremental algorithm for estimating an optimal decision strategy in an infinite-horizon decision problem, now refers to a general class of reinforcement learning methods widely used in statistics and artificial intelligence.Popular reinforcement learning algorithm used to find the optimal action-selection policy for a given finite Markov decision process (MDP). Q-learning has widespread applications because Q-learning converges to an optimal policy, no matter what the agent does, as long as it tries each action in each state enough. The primary goal of Q-Learning is to learn a policy, represented by a function Q(s,a), that assigns a value to each state-action pair. This value represents the expected cumulative reward the agent will receive when taking action a in state s and following the optimal policy thereafter. The formula to update Q-values is:

$Q[s,a]:=Q[s,a]+\alpha (r+\gamma \max _{a'}Q[s',a']-Q[s,a]),s:=s'$

Where:

- $Q[s,a]$ is the Q-value for state s and action a.

- $\alpha$ is the learning rate, representing the weight given to the new information. It is a value between 0 and 1 and could be a function of the number of iterations.

- r is the reward the agent gets after taking action a in state s.

- $\gamma$ is the discount factor, representing the agent's preference for future rewards. It is a value between 0 and 1.

- $s'$ is the next state resulting from taking action a in state s.

- $\max _{a'}Q[s',a']$is the maximum Q-value over all possible actions in the next state $s'$

The function that we choose for the parameter $\alpha$ can seriously affect the performance of our agent. Not only can it determine if the agent converges, but also it can impact how fast the agent converges.

Theoretical study of Alpha functions

To begin with, we introduce Robbins-Monro Conditions. They are a set of mathematical conditions that are important for ensuring the convergence of stochastic approximation algorithms, including Q-learning. Specifically, when we apply Robbins-Monro Conditions to $\alpha$ function, we want to guarantee that the algorithm converges to the optimal Q-values. In this context, these conditions are:

• Stationary:

1.$\sum _{k=1}^{\infty }\alpha _{k}=\infty$

2.$\sum _{k=1}^{\infty }\alpha _{k}^{2}<\infty$

• Randomness:

The sequence $\{\alpha _{k}\}$ must be a sequence of independent random variables.

Obviously, the Randomness condition is satisfied when implemented in Q-learning formula. Consequently, we just need to check if our proposed $\alpha$ functions satisfy the Stationary condition.

1. $\alpha _{k}={\frac {1}{k}}$

To see if this $\alpha$ function converges in Q-learning, first, we need to investigate if the series $\sum _{k=1}^{\infty }{\frac {1}{k}}$ diverges to satisfy Robbins-Monro' stationary condition's first part. This is a benchmark problem in calculus and it can be proven that it diverges. For the second part of the stationary condition, we have to prove that the series $\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}$ converges. This has been proven by Euler on 1734. As a result, we can infer that this $\alpha$ function theoretically converges to optimal Q-values when implemented.

2. $\alpha _{k}={\frac {10}{9+k}}$

Clearly, this $\alpha$ function has the same behavior as the previous one. Multiplying a series term by a constant has no effect on its convergence behavior (you can factorize the constant and take it out of the summation). Adding a constant to the denominator is equivalent to a shift in the x-axis direction. Consequently, we can say that this $\alpha$ function satisfies stationary conditions as well. This means that it theoretically converges to the optimal Q-values.

3. $\alpha _{k}={\frac {5\ln(k)}{k+1}}$

Mathematically speaking, this function does look a bit different from the previous ones. To check if it satisfies the stationary condition we used Ermakoff's test. This test looks a bit tricky to carry out by hand. Thus, we used a Matlab package to automatically give us the result of the test. The results indicate that $\sum _{k=1}^{\infty }{\frac {5\ln(k)}{k+1}}$ diverges and $\sum _{k=1}^{\infty }\left({\frac {5\ln(k)}{k+1}}\right)^{2}$ converges. In other words, we theoretically ensure that this $\alpha$ function causes the Q-learning agent to converge to optimal Q-values.

Practical study of Alpha functions

Q-learning hyperparameters

It is important to note that for all the alpha values, we used the same hyperparameters for our Q-learning agent. They are listed below:

1. $\gamma$=0.9
2. Initial Q-values are zero.
3. Exploration Strategy: Epsilon Greedy with $\epsilon =0.2$

We can progress through the game either by choosing the next action manually or automatically by specifying the number of steps to do the action. The action done automatically is chosen by the agent to be the one with the optimal Q-value. But, sometimes to explore other policies the model chooses to do another action. $\epsilon$ value of 0.2 indicates that with a probability of 0.2, the agent will do a random action instead of the action determined by the optimal policy. This can help the agent explore different actions in different states to better update Q-values.

MDPtiny game

The GUI to visualize MDPtiny problem. The arrows show the actions and the numbers show the Q-values.

To check if these $\alpha$ functions work in practice as well, we need to implement them on a problem. MDPtiny looks like a good candidate. There are six states and 4 actions. "The state is represented as (x, y) where x counts from zero from the left, and y counts from zero upwards, so the state (0, 0) is on the bottom-left state. The actions are upC for up-careful, upR for up-risky, left, and right". You can see a visualization of this problem.

The up, down, left, and right arrows indicate UpR, UpC, left, and right actions respectively. The numbers on the arrows show the Q-values corresponding to that action in current state.

Convergence conditions

To ensure that our Q-learning agent converges on our problem, we need to check two conditions: First, our Q-values should be as stable as possible. Second, The optimal policies should be stable too. However, having these two cannot guarantee that our agent converges to the optimal Q-values. As a result, we need to have a ground truth for optimal Q-values to compare our final Q-values with them. For this problem, we considered Value Iteration (VI) algorithm. Thus, you can see our "True" optimal Q-values that our agent is intended to reach below:

Ground true optimal Q-values and policies

Now we are ready to see practical implementations of the proposed $\alpha$ functions.

Alpha functions implementation

1. $\alpha _{k}={\frac {1}{k}}$

For this value of $\alpha$, our agent could not converge in practice. Although the optimal policies converge to the true ones, the Q-values could not converge to our ground truth after a large number of steps. You can see the results below:

Final Q-values and policies with alpha function:1/k

2. $\alpha _{k}={\frac {10}{9+k}}$

This $\alpha$ function works well on MDPtiny problem in practice. It converges in reasonable number of steps and the final Q-values match our ground truth with good precision. You can see the results below:

Final Q-values and policies with alpha function:10/(9+k)

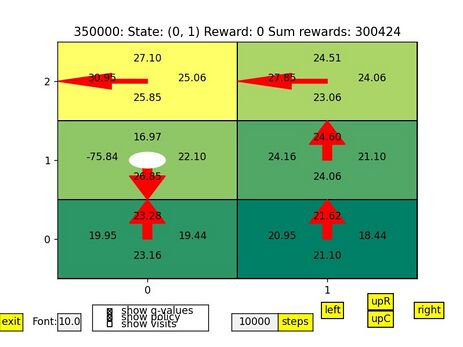
3. $\alpha _{k}={\frac {5\ln(k)}{k+1}}$

This innovative $\alpha$ function works on our problem too. The resulting Q-values of this $\alpha$ function greatly match the ground truth. The results are below:

Final Q-values and policies with alpha function:5ln(k)/(k+1)

Conclusion

On this page, we started by reviewing Q-learning important concepts. Then, we introduced Robbins-Monro Conditions to theoretically check whether an agent with a specific $\alpha$ function converges. We proposed three different $\alpha$ functions, and first, we investigated them through theory. The theoretical conditions predict that all of those three $\alpha$ functions converge. Then, we implement those functions on an MDP problem called MDPtiny to check their practical performance. The results showed that for $\alpha _{k}={\frac {1}{k}}$, the Q-learning agent does not converge in practice. But, for the other two, it converges both in practice and theory.

To Add

Put links and content here to be added. This does not need to be organized, and will not be graded as part of the page. If you find something that might be useful for a page, feel free to put it here.