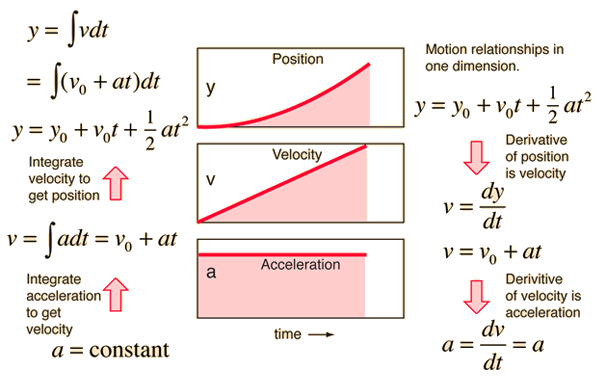
Acceleration Velocity Position

This article is part of the PhysicsHelp Tutoring Wiki

There are some interesting pointers in these three graphs that will likely help you understand how kinematics relate to mathematics. Bare with me and see if you can follow my lesson. First remember that position, velocity and acceleration are related by means of differentiation and intergration. When I look at the image above I tend to scan the three graphs for one that I understand instantly. It isn't the position graph, it's not the velocity graph either. It's the acceleration graph because it's a constant. If the acceleration is constant than the velocity will be increasing linearly. Try to see this intuitively; If a car is accelerating at 1m/s per second (1m/(s^2)) then its velocity will increase by 1m/s each second. That is the princilple that the velocity and acceleration graphs are showing. Now, to move from the velocity graph to the position graph the same sort of reasoning can be applied. If, after each second the cars velocity is increasing by 1m/s then we can see how the car's position will change. After one second it is going 1m/s, after 2s --> 2m/s, 3 -->3m/s and so on. So to determine the position, approximately, by treating the velocity as a constant over each, one second, interval we sum the distance travelled after each second. After one second --> 1m, 2s --> 1+2=3m, 3s -->1+2+3=6m and so on. Stare at the image for a few minutes and try to think of how one graph relates to the other (position/velocity or velocity/acceleration).

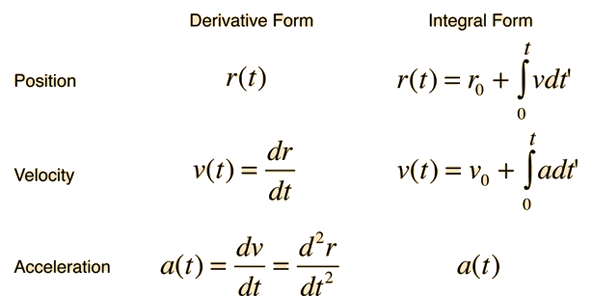
Next up is a little math to get us going. No one I know enjoys doing math as much as, lets say, lying in the sun, but it is the core of physical science and if it weren't for math the value of science would be far less. The image above is an illustration of how we can relate position, velocity and acceleration mathematically. Try to follow these equations. You will use these tools many times during your time here at school so it is important to get good at them quickly to make things easier for you in the future. Believe me it does get easier with practice. Before going through all the mathematics, however, it is easier to understand if you know the definitions of each of the terms. Acceleration is the rate at which velocity changes (so you would expect the slope of a velocity v.s. time graph to be the instantenuous acceleration of the object). Similarly, velocity is the rate at which an object's position changes (so you would expect the slope of a position v.s. time graph to be the instantenuous velocity of the object).

• Back to PhysicsHelp