Science:Math Exam Resources/Courses/MATH215/December 2013/Question 06 (b)/Solution 1

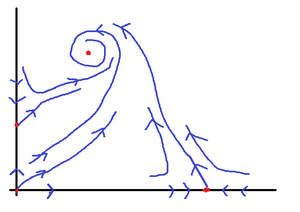
We will need to analyze the linearized system at each critical point.

At (x,y) = (0,0)

$J={\begin{pmatrix}3&0\\0&1\end{pmatrix}}$

which has eigenvectors $(1,0)^{T}$ and $(0,1)^{T}$ with corresponding eigenvalues 3 and 1 respectively. The local solution structure centred at (0,0) is

${\begin{pmatrix}x\\y\end{pmatrix}}=C_{1}{\begin{pmatrix}1\\0\end{pmatrix}}e^{3t}+C_{2}{\begin{pmatrix}0\\1\end{pmatrix}}e^{t}$

Along both eigenvectors, the trajectories move away, with the $(1,0)^{T}$ direction being dominant, since it is multiplied by the larger term, e^3t.

At (x,y) = (0,1)

$J={\begin{pmatrix}2&0\\1&-1\end{pmatrix}}.$

To find the eigenvector corresponding to $\lambda =2$, we seek the solution to $(J-2I){\vec {v}}={\vec {0}}$ so that

${\begin{pmatrix}0&0\\1&-3\end{pmatrix}}{\vec {v}}={\vec {0}}$

Or $v_{1}-3v_{2}=0$, so we take ${\vec {v}}=(3,1)^{T}$.

To find the eigenvector corresponding to $\lambda =-1$, we seek the solution to $(J-(-1)I){\vec {v}}={\vec {0}}$ so that

${\begin{pmatrix}1&0\\1&0\end{pmatrix}}{\vec {v}}={\vec {0}}$

Or v₁ = 0, v₂ = anything, so we take ${\vec {v}}=(0,1)^{T}$.

The local solution structure centred at (0,1) is

${\begin{pmatrix}x\\y\end{pmatrix}}=C_{1}{\begin{pmatrix}3\\1\end{pmatrix}}e^{2t}+{\begin{pmatrix}0\\1\end{pmatrix}}e^{-t}$

The solution grows exponentially along the $(3,1)^{T}$ direction and decays exponentially along the $(0,1)^{T}$ direction. Starting anywhere other than along the $(0,1)^{T}$ vector, the solution will approach the $(3,1)^{T}$ vector.

At (x,y) = (3,0)

$J={\begin{pmatrix}-3&-3\\0&4\end{pmatrix}}.$

To find the eigenvector corresponding to $\lambda =-3$, we seek the solution to $(J-(-3)I){\vec {v}}={\vec {0}}$ so that

${\begin{pmatrix}0&-3\\0&7\end{pmatrix}}{\vec {v}}={\vec {0}}$

Or v₂ = 0, v₁ = anything, so we take ${\vec {v}}=(1,0)^{T}$.

To find the eigenvector corresponding to $\lambda =4$, we seek the solution to $(J-4I){\vec {v}}={\vec {0}}$ so that

${\begin{pmatrix}-7&-3\\0&0\end{pmatrix}}{\vec {v}}={\vec {0}}$

Or $-7v_{1}-3v_{2}=0$, so we take ${\vec {v}}=(-3,7)^{T}$.

The local solution structure centred at (3,0) is

${\begin{pmatrix}x\\y\end{pmatrix}}=C_{1}{\begin{pmatrix}1\\0\end{pmatrix}}e^{-3t}+{\begin{pmatrix}-3\\7\end{pmatrix}}e^{4t}$

The solution grows exponentially along the $(-3,7)^{T}$ direction and decays exponentially along the $(1,0)^{T}$ direction. Starting anywhere other than along the $(1,0)^{T}$ vector, the solution will approach the $(-3,7)^{T}$ vector.

At (x,y) = (1,2)

$J={\begin{pmatrix}-1&-1\\2&-2\end{pmatrix}}$, which as we saw in part (a) has complex eigenvalues with negative real part. By plugging in a point, say $(1,0)^{T}$ into the local linear system we can determine the direction of the spiral.

${\begin{pmatrix}-1&-1\\2&-2\end{pmatrix}}{\begin{pmatrix}1\\0\end{pmatrix}}={\begin{pmatrix}-1\\2\end{pmatrix}}$

which points up and to the left at (1,0). Therefore the spiral is counterclockwise.

This is all put together in the very rough global phase portrait.