Science:Math Exam Resources/Courses/MATH215/December 2013/Question 03 (a)/Solution 1

We have a homogeneous ODE $\displaystyle x''+2x'+5x=0$ with x(0) = 0, x'(0) = 1.

The roots of the corresponding characteristic polynomial $\lambda ^{2}+2\lambda +5=0$ are $\lambda ={\frac {-2\pm {\sqrt {2^{2}-4(1)(5)}}}{2}}={\frac {-2\pm {\sqrt {-16}}}{2}}={\frac {-2\pm 4i}{2}}=-1\pm 2i.$

The roots are complex, and we have a general solution of

$\displaystyle x(t)=C_{1}e^{-t}\sin(2t)+C_{2}e^{-t}\cos(2t)$

We can use the initial conditions to find the constants. $x(0)=0+C_{2}=0$ implies $C_{2}=0$. Next, use the fact that the second term vanishes to calculate the first derivative of the solution.

$\displaystyle x'(t)=-C_{1}e^{-t}\sin(2t)+2C_{1}e^{-t}\cos(2t)=2C_{1}$

Since x'(0) = 1 this implies $C_{1}=1/2$. The final solution is therefore

$x(t)={\frac {1}{2}}e^{-t}\sin(2t).$

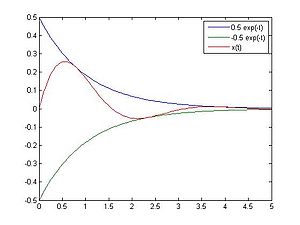
A plot of the solution is given below. Note that the solution is bounded between $x(t)=\pm {\frac {1}{2}}e^{-t}$ so there is an envelope. The solution must fit between the upper and lower envelope functions. At $t=0$, $x=0$, and the solution is increasing at $t=0$ (the derivative is positive).