Science:Math Exam Resources/Courses/MATH215/December 2011/Question 07 (c)/Solution 1

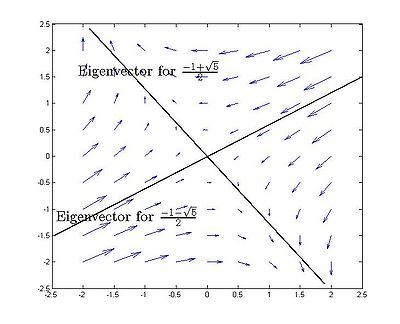
Using the Jacobian from 7 (b) we find the linearization of the system in the critical points.

Critical point $y_{0} = (0, 0)$

J (0, 0) = (\begin{matrix} 2 & 0 \\ 0 & 1 \end{matrix}) .

This matrix is diagonal and so the diagonal elements are the eigenvalues
This matrix is positive definite since its two eigenvalues $1, 2$ are positive. All positive eigenvalues indicate that the critical point $(0, 0)$ is an unstable node.
The eigenvector for the eigenvalue $1$ is $(\begin{matrix} 0 \\ 1 \end{matrix})$ .
The eigenvector for the eigenvalue $2$ is $(\begin{matrix} 1 \\ 0 \end{matrix})$ .
The linearized critical point in the phase space is on the following figure:

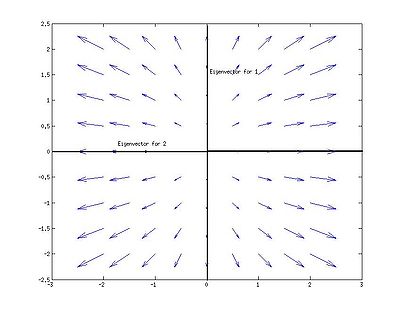
Critical point $y_{0} = (2, 0)$

J (2, 0) = (\begin{matrix} - 2 & - 2 \\ 0 & - 1 \end{matrix}) .

The eigenvalues are $- 2, - 1$ , because a triangular matrix has its eigenvalues on the diagonal. The eigenvalues are both negative and hence, the matrix is negative definite and this critical point is a stable node.
The eigenvector for the eigenvalue $- 2$ is $(\begin{matrix} 1 \\ 0 \end{matrix})$ because of the triangular shape of the matrix.
For the other eigenvector we need to work a little more and calculate the null space of $J (2, 0) - (- 1 I)$ :

$(J (2, 0) + 1 I) (v_{1}, v_{2})^{T} = (\begin{matrix} - 1 & - 2 \\ 0 & 0 \end{matrix}) (\begin{matrix} v_{1} \\ v_{2} \end{matrix}) = (\begin{matrix} - v_{1} - 2 v_{2} \\ 0 \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix})$

Hence, $v_{1} = - 2 v_{2}$

We find the the eigenvector for $- 1$ is $(\begin{matrix} - 2 \\ 1 \end{matrix})$ .

The linearized critical point in the phase space is on the following figure:

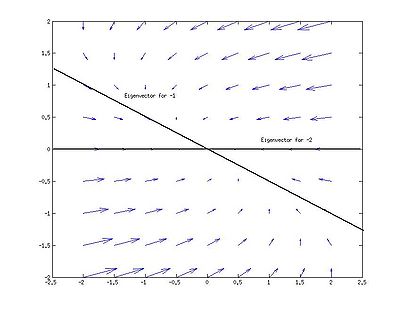
Critical point $y_{0} = (1, 1)$

J (1, 1) = (\begin{matrix} - 1 & - 1 \\ - 1 & 0 \end{matrix}) .

For the eigenvalues we calculate

$d e t (\begin{matrix} - 1 - λ & - 1 \\ - 1 & - λ \end{matrix}) = λ^{2} + λ - 1 = 0$

$λ = \frac{- 1 \pm \sqrt{5}}{2}$

The eigenvalue for $\frac{- 1 - \sqrt{5}}{2}$ is the null space of

$(\begin{matrix} - 1 + \frac{1 + \sqrt{5}}{2} & - 1 \\ - 1 & \frac{1 + \sqrt{5}}{2} \end{matrix}) (\begin{matrix} v_{1} \\ v_{2} \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix})$

$v_{1} = \frac{1 + \sqrt{5}}{2} v_{2}$

so that the eigenvector is $(\begin{matrix} 1 + \sqrt{5} \\ 2 \end{matrix})$ .

The eigenvalue for $\frac{- 1 + \sqrt{5}}{2}$ is the null space of

$(\begin{matrix} - 1 + \frac{1 - \sqrt{5}}{2} & - 1 \\ - 1 & \frac{1 - \sqrt{5}}{2} \end{matrix}) (\begin{matrix} v_{1} \\ v_{2} \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix})$

$v_{1} = \frac{1 - \sqrt{5}}{2} v_{2}$

and the eigenvector is $(\begin{matrix} 1 - \sqrt{5} \\ 2 \end{matrix})$ .

Because one eigenvalue is positive, the other negative, the critical point is not asymptotically stable. Along the eigenvector for $\frac{- 1 + \sqrt{5}}{2}$ , the solution moves away from the critical point, along the eigenvector for $\frac{- 1 - \sqrt{5}}{2}$ , the solution moves towards the critical point. Since the eigenvalues do not have the same sign, the matrix is indefinite and the equilibrium is a saddle point.

See the following figure: