Let  be the line that makes an angle of
be the line that makes an angle of  with the positive
with the positive  -axis, and
-axis, and  be the line that makes an angle of
be the line that makes an angle of  with the positive
with the positive  -axis. We sketch the sequence of reflections below, keeping the original orientation of the axes in the background, labelled as
-axis. We sketch the sequence of reflections below, keeping the original orientation of the axes in the background, labelled as  ,
,  . In the sketch, the image of the
. In the sketch, the image of the  -,
-,  -axes after
-axes after  is labelled as
is labelled as  ,
,  . The reflection
. The reflection  is then applied to the
is then applied to the  -,
-,  -axes, resulting in the
-axes, resulting in the  -,
-,  -axes.
-axes.
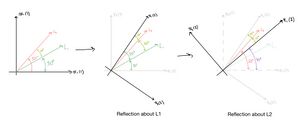
Math 152 2022 Q18 solution figure
After the reflection about  , we now look at the angle between the axes
, we now look at the angle between the axes  and
and  , this is
, this is  (shown in purple). The
(shown in purple). The  - and
- and  -axes are now
-axes are now  off from their original orientation (taking counterclockwise rotation to be positive).
off from their original orientation (taking counterclockwise rotation to be positive).


















