Science:Math Exam Resources/Courses/MATH104/December 2016/Question 11 (d)/Solution 1

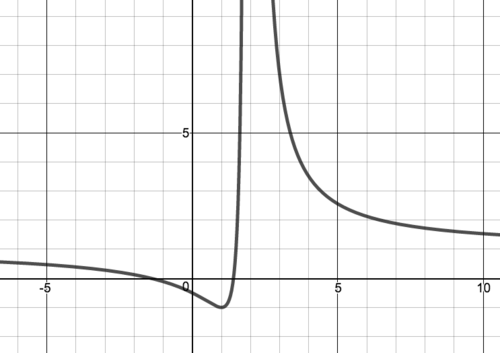
Following the hint, we have

1. The domain of $f$ is $(-\infty ,2),(2,\infty )$ since the denominator of $f$ is $0$ when $x=2$.
2. From (b), we know that the function $f$ has a local minimum at $x=1$. The minimum point is $(1,-1).$
3. From (c), we know that $({\frac {1}{2}},-{\frac {7}{9}})$ is the only inflection point.
4. From (a), we know that the vertical asymptote of $f$ is $x=2.$
5. By considering the limits $\lim _{x\to -\infty }f(x)$ and $\lim _{x\to \infty }f(x)$, we know that the horizontal asymptote is $y=1$. Details can be found in solution to part (a).
6. From (b), we know that $f$ is increasing on $(1,2)$ and decreasing on $(-\infty ,1),(2,\infty ).$ From (c), we know that the function is concave up on $({\frac {1}{2}},2),(2,\infty )$ and concave down on $(-\infty ,{\frac {1}{2}}).$
7. Label the critical point $(1,-1)$ , the inflection point $({\frac {1}{2}},-{\frac {7}{9}})$ and the vertical asymptote $x=2$on the real line. Connect these points with curves exhibiting the proper concavity.