Science:Math Exam Resources/Courses/MATH102/December 2012/Question C 05 1/Solution 1

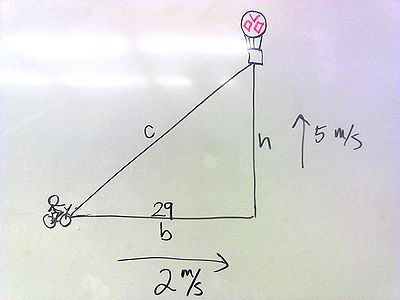
We will start by drawing a picture relating the different facts given in the problem.

Now it is necessary to figure out what the question is asking. This is an optimization problem, where the thing being optimized is the rate at which $\theta$ is changing, or $d\theta /dt$. So our next step is to actually find an expression for this rate.

We start by relating all the information we already have in the question. The diagram shows a right triangle, with adjacent and opposite sides labeled. Thus, the best way to relate the information is the tangent function.

$\tan \theta =h/b$

We can express the height of the balloon as a function of time. Since it is rising at a rate of 5 m/s, the height of the balloon can be given as $h(t)=5t$. Similarly, the distance of the girl from the ballon's liftoff point can be given as the initial distance, minus her rate of travel, or $b(t)=29-2t$. Plugging these into the formula, we get:

$\tan \theta ={\frac {5t}{29-2t}}$

Differentiating with respect to time (t) gives:

$\sec ^{2}\theta {\frac {d\theta }{dt}}={\frac {5(29-2t)-5t(-2)}{(29-2t)^{2}}}$

We want our final expression to be in terms of $t$, so we want to change the $\sec ^{2}\theta$ into an expression in terms of t. We will do this by going back to the definition of $\sec \theta$ as a trig ratio. We recall $\sec \theta$ is the ratio of hypotenuse over adjacent, or $c/b$ in our notation. In particular, we have $\sec ^{2}\theta =c^{2}/b^{2}$. The adjacent side b is given by $29-2t$ and we can use the Pythagorean theorem to find the hypotenuse $c^{2}$.

$c^{2}=(5t)^{2}+(29-2t)^{2}$

So we have

$\sec ^{2}\theta ={\frac {(5t)^{2}+(29-2t)^{2}}{(29-2t)^{2}}}$

Replacing $\sec ^{2}\theta$ in our original equation, we get:

${\frac {(5t)^{2}+(29-2t)^{2}}{(29-2t)^{2}}}{\frac {d\theta }{dt}}={\frac {5(29-2t)-5t(-2)}{(29-2t)^{2}}}$

We want to solve this expression for $d\theta /dt$. Simplifying the above expression, we get:

${\frac {d\theta }{dt}}={\frac {145}{(5t)^{2}+(29-2t)^{2}}}$

Now we finally have an expression for $d\theta /dt$. To complete the problem, we must find where it is at a maximum. To do so, we will use our usual method for finding a maximum: differentiating, finding critical points, and testing whether it is a maximum.

Taking the derivative gives with respect to t gives:

${\begin{aligned}{\frac {d^{2}\theta }{dt^{2}}}&={\frac {-145(2(5t)(5)+2(29-2t)(-2))}{((5t)^{2}+(29-2t)^{2})^{2}}}\\&={\frac {-145(50t-116+8t)}{((5t)^{2}+(29-2t)^{2})^{2}}}\\&={\frac {-145(58t-116)}{((5t)^{2}+(29-2t)^{2})^{2}}}\\&={\frac {-145\cdot 58(t-2)}{((5t)^{2}+(29-2t)^{2})^{2}}}\end{aligned}}$

We are free to ignore the denominator, as it is always positive, thus never makes the derivative undefined. We can therefore restrict our attention to the numerator, set it equal to zero, and solve for t. This gives $t=2$. It remains to show that this point is a maximum. The easiest way to do this is the first derivative test; that is choosing two points on either side of our critical point $t=2$ and checking if the sign of the derivative changes. Again, the denominator of the derivative is always positive, so we need only consider the numerator:

	t < 2	t = 2	t > 2
$d^{2}\theta /dt^{2}$	+	0	-

This indicates that the original rate $d\theta /dt$ changes from increasing to decreasing at $t=2$, meaning that it is indeed the maximum we're looking for. The time at which the angle $\theta$ is increasing the fastest is at $t=2$ seconds after the balloon is released.