Science:Math Exam Resources/Courses/MATH101/April 2010/Question 02 (a)/Solution 1

We see the function and a sketch of the volume in the following figure.

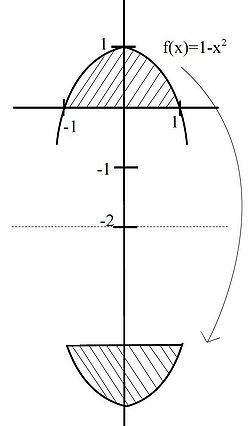
We use the shell method

$V=2\pi \int h(z)z\,dz$

to find the volume. Therefore we need to determine what is the height $h(z)$ and what is the integral variable $z$.

On the next figure we see, that the height is the inverse of the function

$y=f(x)=1-x^{2}.$

And for this height the integral variable $z$ is the distance from $y$ to the rotating axis, which is $y=-2.$

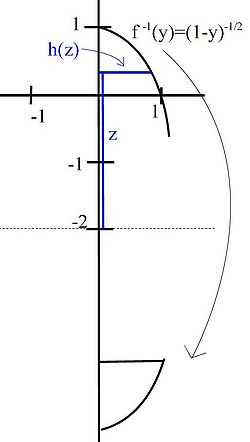
So, we find z = y + 2 and for the height we calculate

$f(x)=y=1-x^{2}\$

$x^{2}=1-y\$

$f^{-1}(y)=x={\sqrt {1-y}}.\$

For convenience, we calculate half of the volume and drop the left half. Then we can take

$\displaystyle h(z)={\sqrt {1-y}}$

for z = y + 2.

The boundaries of the integral must be the left and right edge of the interval for $y=[0,1]$. Now we need to calculate the integral

${\begin{aligned}{\frac {1}{2}}V&=2\pi \int h(z)z\,dz\\&=2\pi \int _{0}^{1}(y+2){\sqrt {1-y}}\,dy\\&=2\pi \overbrace {\int _{0}^{1}\underbrace {y} _{=u}\underbrace {\sqrt {1-y}} _{=dv}\,dy} ^{\text{use integration by parts}}+2\pi \int _{0}^{1}2{\sqrt {1-y}}\,dy\\&=2\pi \left[y(1-y)^{\frac {3}{2}}(-{\frac {2}{3}})\right]_{0}^{1}+2\pi {\frac {2}{3}}\int _{0}^{1}(1-y)^{\frac {3}{2}}\,dy+2\pi 2\left[(1-y)^{\frac {3}{2}}\right]_{0}^{1}\\&=0+2\pi {\frac {2}{3}}\left[(1-y)^{\frac {5}{2}}(-{\frac {2}{5}})\right]_{0}^{1}-0+2\pi {\frac {4}{3}}\\&=2\pi {\frac {4}{15}}+2\pi {\frac {4}{3}}\\&={\frac {16\pi }{5}}\end{aligned}}$

So, we get for the volume

$V={\frac {32\pi }{5}}.$