Science:Math Exam Resources/Courses/MATH100/December 2016/Question 12/Solution 1

The diagram of the cylinder inside the cone is as the following

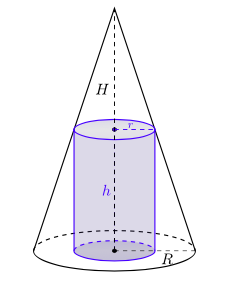cylinder in a cone

where $R=1$ m and $H=2$ m are the base radius and height of the cone.

The two right riangles in the diagram are similar, so we have the following ratios:

$\begin{array}{rl}\frac{r}{R}=\frac{H-h}{H}& \Rightarrow \frac{r}{1}=\frac{2-h}{2}\\ & \Rightarrow r=\frac{1}{2}(2-h),0<r<1,0<h<2\end{array}$

Now we know that the volume of the cylinder is the area of the base times height i.e.

$V=\pi r^{2}h=\frac{\pi }{4}h(2-h{)}^2=\frac{\pi }{4}(4h-4h^2+h^3)$

To maximize the volume we need to find the critical points of $V$. We use the power rule to get

$V^{\prime }(h)=\frac{\pi }{4}(3h^2-8h+4)=0$

Using the quadratic formula (or factoring) gives $h=2,h=\frac{2}{3}$. For $h=2$ the volume becomes 0, so the maximum must be attained at $h=\frac{2}{3}$, and hence $r=\frac{1}{2}(2-\frac{2}{3})=\frac{2}{3}$, therefore,

$V=\pi \times \frac{4}{9}\times \frac{2}{3}=\frac{8}{27}\pi$

Note that in general, we need to check the endpoints for $h$ or $r$, where in this example make the volume equal to 0.

The dimension of the cylinder is therefore $h=\frac{2}{3},r=\frac{2}{3}$.