Science:MATH105 Probability/Lesson 2 CRV/2.09 Additional PDF Example

A Geometric Problem

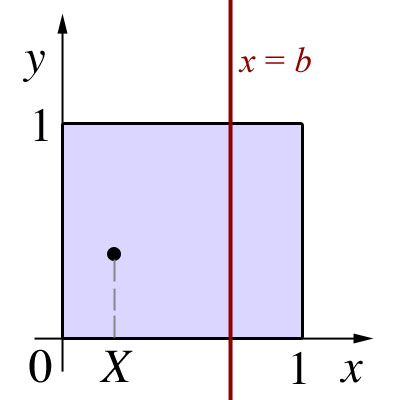
Consider the square in the xy-plane bounded by the lines x = 0, x = 1, y = 0 and y = 1. Now consider a vertical line with equation x = c, where 0 ≤ c ≤ 1 is fixed. Note that this line will intersect the unit square defined previously.

Suppose we select a point inside this square, uniformly at random. If we let X be the x-coordinate of this random point, what is the probability that X is in the interval [0 , c]?

An illustration of our problem is given in the figure below. Graphically, we are trying to find the probability that a randomly selected point inside the square lies to the left of the red line.

Let's begin by considering two cases:

• Case 1: Find Pr(0 ≤ X ≤ c) if c = 1
• Case 2: Find Pr(0 ≤ X ≤ c) if c is in the interval [0, 1)

Case 1

If c = 1, then the random point must certainly have x-coordinate between 0 and c. The area to the left of the red line is the entire area of the square, and our random point has to lie inside the square. Thus, we are certain to find the x-coordinate in the interval [0,1]; i.e. Pr(0 ≤ X ≤ c) = Pr(0 ≤ X ≤ 1) = 1.

Case 2

The region to the left of the red line is a rectangle with area equal to c. The probability that our random point lies inside this rectangle is proportional to the area of that rectangle, since the larger the area of the rectangle, the larger the probability that the point is inside of it.

Thinking of probabilities in terms of areas, consider the following cases:

• if the probability that the point is between 0 and c were equal to 0.50, then the red line would have to divide the square into two equal halves: c = 0.5
• if the probability that the point is between 0 and c were equal to 0.25, then the red line would have to divide the square at 1/4: c = 0.25
• if the probability that the point is between 0 and c were equal to 0.10, then the red line would have to divide the square at 1/10: c = 0.1

In general, it is clear that we should have Pr(0 ≤ X ≤ c) = c.

Notice that this result matches with the definition of our random variable X. Recall that we wanted to select a random point uniformly at random from the unit square. Thus the random variable X giving the x-coordinate of this random point should be a continuous uniform random variable on the interval [0,1]. We have already seen that the PDF of a general uniform random variable defined on a generic interval [a,b] is

$f(x)={\frac {1}{b-a}},{\text{ where }}a\leq x\leq b.$

Thus, the CDF of a generic uniform random variable is

$F(x)=\int _{a}^{x}{\frac {1}{b-a}}dt={\frac {x-a}{b-a}}{\text{ for }}a\leq x\leq b.$

For the example under examination, we have a = 0 and b = 1. Therefore, Pr(0 ≤ X ≤ c) = Pr(X ≤ c) - Pr(X ≤ 0) = c, which agrees with the answer we derived using purely geometric considerations.