Science:MATH105 Probability/Lesson 2 CRV/2.04 Continuous Random Variables
The distinction between continuous and random variables can now be made more precise by using the CDF.
| Definition: Continuous Random Variable |
|---|
|
Let X denote a random variable with distribution function F(x). The random variable X is a continuous random variable if its CDF, F, is continuous. |
It is by definition that continuous CDFs of a random variable are CDFs of continuous random variables.
In our prior grade distribution example, the CDF was not continuous and so it corresponded to a discrete random variable that represented a grade. Whereas our previous temperature example, the CDF was continuous, the random variable was a continuous random variable that represented a temperature.
Example
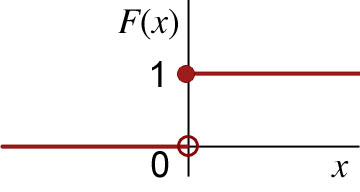
Consider the function whose graph is given below.
This function cannot represent a cumulative distribution function for a continuous random variable because F is not continuous for all values of x. However, F could represent a cumulative distribution function, because the limit as x goes to negative and positive infinity are 0 and 1, respectively.