Science:Infinite Series Module/Units/Unit 3/3.1 Power Series/3.1.02 The Power Series
Indeed, a there is a more general representation for the series we introduced on the previous page:
The more general representation is given by the following definition.
| Definition: Power Series |
|---|
| An infinite series of the form
where c is a constant, is a power series about c. The constants, ak are referred to as the coefficients of the series. |
What Is A Power Series?
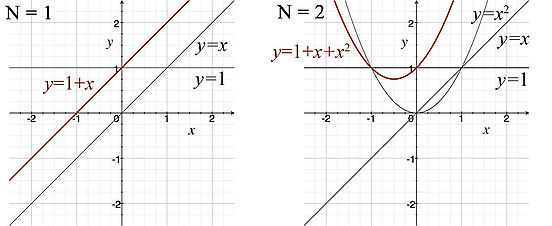
It may help to consider a simple example with partial sums. Let's take the case where ak = 1, and c = 0, which gives us
If we let N = 1, then we have a polynomial of order 1
If we take N = 2, then we have a polynomial of order 2
Similarly, with N = 3, then we would obtain a polynomial of order 3
In the limit as N goes to infinity, we obtain a power series.
The figure below provides a graphical explanation of what a power series is: an infinite polynomial.