WEEKS 2 & 3: Part I: Getting Started with R

On Lab Computers: Login and create a folder

To login, write your CWL login name followed by ".stu" (e.g: myCWL.stu)

Each student needs to create a personal folder to save work and datasets. You will see other student´s folders, but you will only be able to open your own.

1. Click the file explorer in the bottom toolbar.
2. Click on "This PC" icon.
3. Open the icon named "scratch".
4. Open LFS252.002
5. Create a folder, for example: Firstname Lastname.

On Laptops and Personal Computers: Download R and R Studio

Download R

1. Visit: https://www.r-project.org/
2. Click on the “Download R” link in the first paragraph.
3. Chose a location. Being in Vancouver, you should select the SFU location, under 'Canada'.
4. Select Mac or Windows.

Mac: click on the “R-3.6.2.pkg”
Windows: click the “install R for the first time” link. Then click the “Download R 3.6.2 for windows” link.

5. Once downloaded, install the software.

Download RStudio

Once you have downloaded R, you can download RStudio. RStudio is a user friendly intergrated development environment for R.

1. Visit: https://rstudio.com/products/rstudio/download/.
2. Click on the “Download RStudio” link.
3. Click on the “Download” button under RStudio Desktop link.
4. From the “All Installers” section, select link under "Download" that is appropriate for you (e.g. Mac, Windows, etc.)
6. Once downloaded, install the software.

Open the RStudio Interface

You should see 3 windows:

Console

You can type your commands here and press the "Enter" key to execute your command. Your answers will appear in this window.

For example, type 2+2 and press the "Enter" key.

Environment/History

Environment: you can see the data that you have imported, the values that you created, etc.
History: you can view all of your previous commands.

Files/Plots/Packages/Help/Viewer

Help: This tab will probably be your best friend. You might find it a bit tricky at first to understand the information given there, but you will get used to it. You can use the search bar (the bar on the top right corner of the 'Help' window that has a magnifying glass) to enter what you are looking for (e.g. mean) and press 'Enter' (you might have to press 'Enter' twice, depending on the computer).
Plots: The graphs that you will be creating will appear in this tab. We will learn more about this tab as we go on.
We will learn more about the other tabs as we go on.

You can open a fourth window: an R script. See below for the details:

R scripts

Instead of writing your commands in the console, is useful to write them in the script (similar to a text editor). The advantage of using an R script is that you can easily edit, save, and share your work.

On the top left corner there is an icon of a white page with a plus sign in a green circle. Click on it, and then click on the first option: 'R script' to open a script. A short cut to open a script is: Ctrl+Shift+N. To run a command from the script you need to keep the cursor on the same line as the command you want to run and press Ctrl+Enter or click the “Run” button in the top right corner of the R script. If you want to run many lines at the same time, highlight them all and then press Ctrl+Enter or click the “Run” button.

Common mistakes when running commands from the script: highlighting just a part of the code or placing the cursor in an incorrect line. If you get an ERROR message from R, always verify that you highlighted all the code you want to run or placed the cursor in the correct line (this will make more sense later on).

Getting familiar with R

This section is adapted from this workshop

Let's use an R script to do the exercises in this section.

Running Commands in R scripts

Remember that to run your commands, you need to press Ctrl+Enter or click the “Run” button in the top right corner of the R script, keeping your cursor on the same line as the command you want to run. If you want to run many lines at the same time, highlight them all and then press Ctrl+Enter or click the “Run” button.

Note: To make notes on your script, place " # " before your note. In the script, within a line, everything that comes after " # " is considered a note and will not run. If you want to finish a note, simply start a new line. If you want to start a new line but continue your note, place "#" again.

Arithmetic

R can be used as a calculator. Let’s try some arithmetic. Type the following command:

3+4

and then run it. You should see the following appearing in the console:
> 3+4
[1] 7

the '>' indicates the command that was run. The output from our operation is '7'. The '[1]' that precedes it is part of R's printed output to the console; the '[1]' indicates that your output is a vector and this is the first element of that vector. (Indeed, 7 is the only element in this vector.) You can ignore all this for now; it will make more sense to you soon.

Let's repeat the previous steps for different arithmetic:
Type the following command in your script:

3-4

After running it, you should see:
> 3-4
[1] -1

and so on...

3*4
3/4
3^4

Symbols like * / and ^ are know as "arithmetic operators"

See this page for more arithmetic operators and functions in R.

Objects

When doing calculations you can save them as 'objects' so you can use them further down the road.
Objects can contain single values, vectors (data in one column or row), character strings, and data matrices of two or more vectors, etc. generally known as data structures. An object can also be "NULL" which means that is empty.

Creating Objects

The basic structure to create an 'object' in R, is the following:

objectName <- value

The arrow points to the object that is receiving the input. Everything to the right of the arrow will be contained within the object. In this example "objectName" is the name of the object, is created by you and could be any name you want (with restrictions addressed later on), and "value" is what you want to store in the "objectName".
Here is an example:

x <- 3 * 4

You have assigned the value of 12 (3*4 = 12) to the object 'x'. This:
> x <- 3 * 4
will appeared in the console.
If you look in the 'Environment' you will see that the object 'x' was created, which has an associated value of 12.

To view your object in the console, you need to 'call' it:

Displaying the Content of Objects

1. To display the content/call/see/inspect (the 4 terms will be used interchangeably) by entering and running its name:

You should get the following result in the console:
[1] 12
2. You could also place the command in brackets, and R will save the object and display its content all at once. Here is an example. Type and run the following command:

(z <- 5+4)

You should see this in the console:
> (z <- 5+4)
[1] 9
3. You could also use the semicolon and write the name of the object right after the command:

w <- 85*9/52; w

You should see this in the console:
> w <- 85*9/52; w [1] 14.71154

More about Creating Objects

Overwriting Objects

If the object ('x' in this case) already exists, it will be overwritten when you assign a new value to it and the old content will be lost. Write and run this command as an example:

x <- 3 + 4

Let's call 'x' now. Write and run this command:

You should get this answer in the console '[1] 7'. Therefore, 'x' now has an assigned value of 7, not 12 anymore.
To avoid overwriting, use different names for the subsequent objects you create.
Tip:When you name your objects, use names that are descriptive.

R is Case Sensitive

R is case sensitive. For example, 'x' and 'X' are not the same object. Try to run these commands as an example.

x <- 3 * 4
X <- 3 + 4
y <- x + X
y

This should give you: [1] 19

Completion Facility

Write and run the following command:

thisIsAReallyLongName <- 2.5

To inspect it, try R Studio’s completion facility: in your R script, type the first few characters, press 'Tab', add characters until you disambiguate, then press return.
Note: the completion facility would also work in the console.

Objects as Character Strings

Objects can also be character strings. Type and run the following command:

x <- "Hello my name is Rick"

Character strings must be encased in quotes. Otherwise R will interpret a word as an object.

"Hello"

[1] Hello

Undo: Ctlr + Z

If you want to 'undo' something that you typed or erased, you can press 'Ctrl + Z' simultaneously. You can do this as many times as needed.

Redo: Ctlr + Y

Save your Work

As mentioned previously, the advantage of working in an R scripts is that you can easily edit, and save your work and share it with others. When you work in R, make sure that all of the commands needed to obtain the desired outcome is included in the script you are working on (commands to clean the data, to manipulate some variables, to create graphs, etc). Saving your commands is enough; you do not need to save the environment, graphs, variables that you created, as you will simply have to run your script to obtain them again.

To save your script, simply click on the 'floppy disk' icon in the top left corner of the R scripts.
Note: if you are working on the lab computers, a warning message will appear (This operation has been cancelled due to restrictions....).
1. Click OK.
2. Find "This PC" on the left.
3. Click on "scratch".
4. Select "LFS 252.002".
5. Find your folder.

Clear Data, Plots and Console

To avoid confusion, it is recommended that your clear your Environment and plots (graphs) in-between exercises.
By saving your R script you will save all of your work (commands) and there is no need to save your plots/graphs and environment.

Clear the Environment

Type and run this command to clear the Environment and any data stored in arrays and matrices

rm(list=ls())

Note: the command can be entered in the console or in an R scripts.

Instead of entering this command, you can simply use the button depicting a 'broom' at the top of the Environment window.

To delete only one or some of the elements in your Environment, change the default option of 'list' to the 'grid' option from the drop-down menu on the top right corner of the Environment window. Then you will be able to select only the elements that you wish to delete, and press the 'broom' button.
Note: it is suggested to always view the environment using the 'list' format, except when you are cleaning it up.

Clear the Plots/Graphs

Type and run this command to clear the plots (graphs)

dev.off()

Note: the command can be entered in the console or in an R scripts.

If you get an error after running this command, it is probably because you did not have any plot produced.

Instead of entering this command, you can simply use the button depicting a 'broom' at the top of the Plots window.

Clear the Console

Some of you might feel like cleaning their console as well. You can do so by pressing Ctrl + L simultaneously.
Alternately, you can type and run

cat("\014")

Note: the command can be entered in the console or in an R scripts.

Create a Dataset Manually

You can input data in R by creating vector objects (one variable, data matrix of only one row, line, or column) that will appear in the "Values" area o f the Environment, and datasets (data matrix of two or more rows or columns) that appear in the "Data" area of the Environment once created.

For this section, we will use a dataset consisting of the height (measured in centimeters) of 71 students, as follow:
151 154 149 139 151 143 156 160 169
130 171
149 152 174 165 139 134 154
150 157 175 146 177 140 143 190
142 155 142 165 145 159 125
142 139 156 146 149 131 174 121
150 137 147 126 154 129 164 121 135 180
148 159 157 143 145 150 126
142 163 168 136 151 170 145 200 188
163 145 151 173

There are many ways to manually create a dataset in R. Here are two ways:

Combine Values into a Vector or List

Create a variable called 'Height' that will contain all of the different height measurements. Type and run:

Height <- c(151, 154, 149, 139, 151, 143, 156, 160, 169, 130, 171, 149, 152, 174, 165, 139, 134, 154, 150, 157, 175, 146, 177, 140, 143, 190, 142, 155, 142, 165, 145, 159, 125, 142, 139, 156, 146, 149, 131, 174, 121, 150, 137, 147, 126, 154, 129, 164, 121, 135, 180, 148, 159, 157, 143, 145, 150, 126, 142, 163, 168, 136, 151, 170, 145, 200, 188, 163, 145, 151, 173)

In the Environment, you should now see a value called 'Height' with 'num [1:71] 151 154 149 ... ' associated to it.

Let's explain the code:

1. " Height" is the name you gave to the object.
2. Everything to the right of the arrow will be contained in "Height".
3. "c" is our function (combine).
4. The numbers after the function within parenthesis, in this case (151, 154, 149, 139, 151,...), is our argument and/or data.

Scan Command

You can use the scan command (or function) to create an object that contains the 71 observations. Let's create an object called 'Height.2'. Type and run:

Height.2 <- scan()
151 154 149 139 151 143 156 160 169 
130 171
149 152 174 165 139 134 154
150 157 175 146 177 140 143 190
142 155 142 165 145 159 125 
142 139 156 146 149 131 174 121
150 137 147 126 154 129 164 121 135 180
148 159 157 143 145 150 126
142 163 168 136 151 170 145 200 188
163 145 151 173

Note: it is important to have a blank line at the end of the data, to let R know that there is no more data to be scanned. You will have to manually enter that blank line by pressing 'Enter' after having placed your cursor in the console.

In the Environment, you should now see a value called 'Height.2' with 'num [1:71] 151 154 149 ... ' associated to it.
An advantage of using the scan command, is that we did not have to change the format of the data. We could simply copy and paste it after the 'scan()' command.

Remember to clear your Environment and save your R script in between exercises.

Import a Dataset (RDA format)

.rda is the usual file format for saving R objects to file. It is a short for 'RData.'

1. Download the dataset named 'All Countries' from the textbook 'Statistics: Unlocking the Power of Data, Lock.' here (choose the .rda version):
http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true.
Note: if the file does not automatically download to your computer, try right-clicking on the file name and then select the 'Save link as...' option.
2. Save the dataset in a folder of your choice on your computer.
3. Go to R_Studio. In the Environment, click on the icon that depicts a folder with a green arrow (students will be tempted to use the 'Import Dataset' button - you should not use this button when you are using .rda format dataset).
4. Browse your computer to find your dataset.
6. Paste the importing command to your R script so that next time you want to work on this dataset you can simply open your R script and run the command for your dataset to be imported (as long as you leave the dataset in the same folder on your computer). To do so, go in the History tab and you will see that a command was created for importing your dataset. It should be something like this:
load("~/Personal Content/lfs 252/allcountries.rda")
Yours will be different as you saved your dataset in another location than I did.
You might not be able to copy paste the command directly from the History tab. In that case, double click on it in the History and it will appear in the console. Once in the console, you can copy it and paste it in your R script. Do not paste the '<' that appears in front of the command.

To view the dataset, you can double click on it in the Environment, or you can enter and run this command:

View(AllCountries)

You should then see a matrix opening in a new tab in the R script window.

Remember to clear your Environment and save your R script in between exercises.

Import a Dataset (non-RDA format)

You can also import to R datasets that are in other formats, such as CSV. To do this, you need to be a bit more careful.

Depending on the R version you have, the steps to import the CSV dataset will be different, and you may have to update some packages.

If you are working on the computers in the lab:
1. Download the dataset named 'All Countries' from the textbook 'Statistics: Unlocking the Power of Data, Lock.' here (choose the .csv version):
http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true.
Note: if the file does not automatically download to your computer, try right-clicking on the file name and then select the 'Save link as...' option.
2. Save the dataset in your folder on the "scratch" (click OK to the warning message) .
3. In the Environment, click on the “Import Dataset” button. For now, we will only work with Text Files. So click on the “From Text File…” option or CSV (depending on what appears).
4. Browse your computer to the folder where you saved your data and select your dataset.
5. Click “Open”. A popup window should then open.
6. Here is where you need to pay attention. If you don’t choose the options correctly, you will not be able to manipulate the data.

Name: You can rename the dataset as you wish. In this case, let's rename it: all
Encoding: You can leave it to 'Automatic'.
Heading: does your data have a heading? To check this, look in the 'Input File' window on the right of the popup window. Is there a heading (title) in the first row, or does the values start right away? In this case, yes there is a heading, therefore select "yes".
Row names: You can leave it to 'Automatic'.
Separator: what separates the different columns in your dataset? White spaces? Commas? Semicolons? Tabs? Again, look at the 'Input File' window to make sure. In this case, we can see that commas are used to separate the different variables: Country, Code, LandArea, ....
Decimal: Are the decimals separated with a comma or a period? In this case, periods are used.
Quote: Is the dataset using single or double quotes? In this case, double - you can look at the Bahamas entry and you will see that double quotes are used.
Note that sometimes there are no decimals or quotes so that it does not matter which options you choose.
You should always uncheck the “Strings as factor” box.
You should check that the "Data Frame" window shows the data exactly how you want it to be.

7. Click on “Import”
8. Paste the importing command to your R script so that next time you want to work on this dataset you can simply open your R script and run the command for your dataset to be imported (as long as you leave the dataset in the same folder on your computer). To do so, go in the History tab and you will see that a command was created for importing your dataset. It should be something like this:
allcountries <- read.csv("C:/Users/Gabi/Desktop/allcountries.csv")

If you are working on your own computer:
1. Download the dataset named 'All Countries' from the textbook 'Statistics: Unlocking the Power of Data, Lock.' here (choose the .csv version):
http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true.
Note: if the file does not automatically download to your computer, try right-clicking on the file name and then select the 'Save link as...' option.
2. Save the dataset in a folder of your choice on your computer.
3. In the Environment, click on the “Import Dataset” button. Click on the “CSV" option.
Note: the first time you do this, you will get a message saying "Preparing data import requires updated versions of the…" just click yes and the required packages should be installed. If this message appears again in your computer, it means that it has to be installed manually. Your TA will assist you personally to do so. This should be a one time message, and next time you want to import a dataset you will not need to do this again.
4. Browse your computer to the folder where you saved your data and select your dataset.
5. Click “Open”.
6. Click on “Import”.
7. Paste the importing command to your R script so that next time you want to work on this dataset you can simply open your R script and run the command for your dataset to be imported (as long as you leave the dataset in the same folder on your computer). To do so, go in the History tab and you will see that a command was created for importing your dataset. It should be something like this:
allcountries <- read.csv("C:/Users/Gabi/Desktop/allcountries.csv")
Yours will be different as you saved your dataset in another location than I did.
You might not be able to copy paste the command directly from the History tab. In that case, double click on it in the History and it will appear in the console. Once in the console, you can copy it and paste it in your R script. Do not paste the '<' that appears in front of the command.

To view the dataset, you can double click on it in the Environment, or you can enter and run this command:

View(all)

You should then see a matrix opening in a new tab in the R script window.

Remember to clear your Environment and save your R script in between exercises.

Extracting Variables

You will learn to extract (create a vector object), call, and work with (without extracting) single variables from datasets.

You will need to do some manipulation in order to be able to play with the data. There are many ways of doing so, and here are a few.

The following examples will use the 'AllCountries' dataset that we downloaded in the section Import a Dataset .
First, you will need to remove the observations with missing values (NA).

First install the tidyr package by typing the following code into the console:

install.packages("tidyr")

Then in your R script type and run:

library(tidyr)

Run this command to remove all rows with missing (NA) values:

All <- drop_na(all)

Note: If you want to remove the missing values from only some columns but not all then add the names of the desired columns where NAs are to be removed. The command would have the following format:

drop_na(my_dataset, column_name1, column_name2)

where my_dataset would be the name of your dataset, column_name1 is the name of desired column name in from your dataset and so on.

In the Environment, you should now see a Data called 'All' with '77 obs. of 18 variables' associated to it.
You could name the new dataset as you wish, including the same name (AllCountries) which would overwrite the previous dataset.

If we are interested in the variable of life expectancy, we could use one of the two following commands to extract this variable. Type and run:

life_exp <- All$LifeExpectancy

Let's explain the command:
"life_exp" is the name of the object to be created. "All" is the name of the dataset. "LifeExpectancy" is the name of the variable within the dataset. "$" stands for extracting or using elements.
From "All" dataset we want to extract ($) LifeExpectancy, and put it in (<- ) a vector object called " life_exp".
or

life_exp2 <- (All[[14]])

In the Environment, you should now see a value called 'life.exp' and one called 'life.exp2'. Both should have 'num [1:77] 72.4 73.5 80.2 ...' associated to it.
The first command uses the name of the variable (LifeExpectancy) of interest to extract it from the dataset 'All', while the second one uses its position in the dataset (LifeExpectancy is in the 14th column in the dataset).
Both commands create a vector with the data of the variable of interest.

You can now manipulate these variables easily. For example, you could calculate the average, standard deviation and median of life expectancy. Type and run:

mean_life <- mean(life_exp); sd_life<-sd(life_exp); median_life<-median(life_exp)

or

mean_life2 <- mean(life_exp2); sd_life2<-sd(life_exp2); median_life2<-median(life_exp2)

both commands should give you the same answer, as the variables 'life_exp' and 'life_exp2' are the same.
In the Environment, you should now see a value called 'mean.life' and one called 'mean.life2'. Both should have '72.4324675324675' associated to it.

To work with a variable within a dataset without creating a vector object of it, you could also use a command that would combine these two previous steps (extracting and calculating the mean). Type and run:

mean_life3 <- mean(All$LifeExpectancy)

or

mean_life4 <- mean(All[[14]])

Both commands should give you the same result as they simply use different methods to extract the variable of interest. Remember that with "$" the extraction is based on the name of the variable, and with "[[ ]]" on the position of the variable within the dataset. Also remember that the name of the dataset always comes before the dolar sign or brackets.

Remember to clear your Environment and save your R script in between exercises.

Good Code Formatting Practices

This section is adapted from this workshop
1. Object names cannot start with a digit and cannot contain certain other characters such as a comma or a space. You will be wise to adopt a convention for demarcating words in names.
These are good examples:

iUseCamelCase
other.people.use.periods
others_even_use_underscore

Note: the preferred format in R community is the use of underscores.

2. Notice that RStudio surrounds '<-' with spaces. Code is miserable to read on a good day. Give your eyes a break and use spaces.
3. There are two ways to assign values to a variable. You could type and run:

XX <- 3

or

XX = 3

We highly recommend you use the former, even though it is bit more tedious to type. See this article for a discussion of how '<-' and '=' behave differently in some circumstances.

Note: you can save yourself some time by using the following shortcuts that generate ' <- ' (including spaces):

In windows and linux, press alt and the minus sign simultaneously
On Mac OS, press option and the minus sign simultaneously

RStudio offers many handy keyboard shortcuts. Find out more here.

Remember to clear your Environment and save your R script in between exercises.

As you probably noticed from this section, in this wiki the commands are always place in a box, like this:

command

When you see a box, you should understand that it is a command that you should type and run. As of now I will stop repeating these steps: type and run.

Part II: Using R for statistics

WEEK 4: Frequency Distributions and Graphs

Exercise 1
Use the dataset 'AllCountries' that we imported in the Import a Dataset (RDA format) section.

Download the dataset named 'All Countries' from the textbook 'Statistics: Unlocking the Power of Data, Lock.' here (choose the .csv version):

http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true.

Import it to R (refer to the Import a Dataset (RDA format) section if you don't remember how to).
Remember to remove the observations that have missing values. Name the cleaned dataset 'all':

all <- AllCountries[complete.cases(AllCountries),]

Extract the 'LifeExpectancy' variable and name it 'life':

life <- (all$LifeExpectancy)

You are now ready to build a frequency distribution table of the variable 'life expectancy'.

1. Identify the range of the data:

range(life)

The range will appear in the console: (47.9, 82.0)

2. Based on the range, decide how you want to visualize the data (define the width of the classes). Let's expand the range from 40 to 90 and use class width of 10:

breaks <- seq(40,90,by=10)

You should see in the Environment that a value named 'breaks' was created with 'num [1:6] 40 50 60 70...' associated to it.
You can use the the 'Help' tab to learn more about the command 'seq' and its arguments.

3. Break down the data (with the function "cut") into the breaks (classes) that we just defined and name this output 'life.cut':

life.cut <- cut(life,breaks,right="FALSE")

Note: Remember that R is capital sensitive, and TRUE or FALSE need to be written in capital letters.
You can use the the 'Help' tab to learn more about the command 'cut' and its arguments.
You should see in the Environment that a value named 'life.cut' was created with 'Factor w/5 levels " [40 50...' associated to it. You can call this object:

life.cut

Can you make sense of what you see in the console?

4. Summarize the information that you got in the previous step by getting the number of observations that fall within each class (the frequencies):

life.freq <- table(life.cut); life.freq

Note: by adding ' ; life.freq' at the end of the command, we are calling 'life.freq' and its values will be printed in the console.

Frequency Table

5. Produce a table with the frequencies reported in a column:

cbind(life.freq)

"cbind" function combines objects by columns. You can also use the function "rbind" to combine in rows.

Barplot

6. Produce a barplot:

barplot(life.freq)

Produce a graph with titles, axis labels, & colours:

barplot(life.freq,col=rainbow(length(life.freq)),main="Life Expectancy",xlab="Countries",ylab="Frequency")

Remember that you can use the 'Help" tab to learn more about the arguments used in this command.

Histogram

7. You also could have done a histogram:

hist(life,breaks,right=FALSE)

or

hist(life)

Do you notice the difference?

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Additional information/practice questions

We will use the same dataset to create a few graphs.

Ogive

Calculate cumulative frequencies:

cumfreq0 <- c(0,cumsum(life.freq ))

Do you know why we added a zero in this command?

Plot the data

plot(breaks,cumfreq0)

Join the dots

lines(breaks,cumfreq0)

Produce a graph with titles & axis labels:

plot(breaks,cumfreq0,main="Life Expectancy",xlab="Countries",ylab="Cumulative Frequency") 
lines(breaks,cumfreq0)

Remember that you can use the 'Help" tab to learn more about the arguments used in this command.

Remember to clear your Environment and your Plots and to save your R script in between exercises.

WEEKS 5 & 6: Data Description and Visual Analysis

Scatterplots

Scatterplots are a way to visualize the potential relationships between two variables that contain continuous data. This can be a helpful way to visualize potential linear relationships.

Exercise 1

Using the same dataset as before (a cleaned version of "AllCountries"), we can make a scatterplot comparing two continuous, potentially related variables such as life expectancy and degree of health.

1. Plot the data:

plot(all$Health, all$LifeExpectancy)

You can make the scatter plot and line more clear by adding details such as a main title and line colour in a similar manner to bar plots. For instance:

plot(all$Health, all$LifeExpectancy, main = "Comparison between Country Health and Life Expectancy", xlab = "Level of Health", ylab = "Life Expectancy (Age)")

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Exploratory Data Analysis

Exercise 2
Using the following data of the number of flights cancelled in a given city per month for 2015, create a box plot and a five-number summary.

Month	J	F	M	A	M	J	J	A	S	O	N	D
Cancellation	180	39	43	66	10	15	22	30	23	18	53	190

Boxplot

1. Enter the data:

flights <- c(180, 39, 43, 66, 10, 15, 22, 30, 23, 18, 53, 190)

month<- c("J","F","M","A","M","J", "J", "A","S","O","N","D")

flights_data<-data.frame(flights,month)

The data.frame function creates a data frame

2. Create a boxplot:

boxplot(flights_data$flights)

This command produces the default boxplot, on which it is hard to identify the quartiles.

Alternatively, we can customize one:
3. Find the five-number summary:

fivenum(flights_data$flights)

You will see this in the console: [1] 10.0 20.0 34.5 59.5 190.0

This are, in order, minimum value, first quartile, median (second quartile), third quartile, and maximum value.

Note: you can also find a specific percentile from your data by using the function quantile and then specifying the data you want to look at and then the percentile you want to find. For instance, to find the 75th percentile you could use:

quantile(flights_data$flights, 0.75)

4. Create an horizontal boxplot:

boxplot(flights_data$flights, horizontal = TRUE, axes = FALSE)

Note: Use the argument 'horizontal=TRUE' to get an horizontal boxplot and 'axes=FALSE' to get rid of the axes.

5. Add the five-number summary to the boxplot:

text(fivenum(flights_data$flights), labels=fivenum(flights_data$flights), y=1.25)

Note: Use the argument 'y=1.25' to place the values above the boxplot.

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Measures of Central Tendency

Exercise 3
Consider this dataset consisting of the height (measured in centimetres) of 71 students, as follow:
151, 154, 149, 139, 151, 143, 156, 160, 169, 130, 171, 149, 152, 174, 165, 139, 134, 154, 150, 157, 175,
146, 177, 140, 143, 190, 142, 155, 142, 165, 145, 159, 125, 142, 139, 156, 146, 149, 131, 174, 121, 150,
137, 147, 126, 154, 129, 164, 121, 135, 180, 148, 159, 157, 143, 145, 150, 126, 142, 163, 168, 136, 151,
170, 145, 200, 188, 163, 145, 151, 173
Calculate the mean, the median, the mode and the midrange.

Enter the data:

Height <- c(151, 154, 149, 139, 151, 143, 156, 160, 169, 130, 171, 149, 152, 174, 165, 139, 134, 154, 150, 157, 175, 146, 177, 140, 143, 190, 142, 155, 142, 165, 145, 159, 125, 142, 139, 156, 146, 149, 131, 174, 121, 150, 137, 147, 126, 154, 129, 164, 121, 135, 180, 148, 159, 157, 143, 145, 150, 126, 142, 163, 168, 136, 151, 170, 145, 200, 188, 163, 145, 151, 173)

Mean

mean(Height)

151.7606

Median

median(Height)

150

Mode

mode(Height)

"numeric"
This is not what we are looking for! The command 'mode' reports the type of data with which you are working (internal storage mode), not the mode of the data.
We will therefore use a table to find the mode:

table(Height)

You can sort the table to rank the frequencies

sort(table(Height), decreasing=TRUE)

Note: use the argument 'decreasing=FALSE' to obtain an increasing order and 'decreasing=TRUE' for a decreasing order.
The value(s) that has(ve) the highest frequency is(are) the mode, 142, 145 and 151 in this case (with a frequency of 4).

Midrange

R doesn't have a midrange command either, so you need to write the following command in order to obtain the mid range:

mean(range(Height))

160.5

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Weighted Average

Exercise 4
You want to calculate your final grade for one of your courses. You got 88% on your midterm, which is worth 30% of the final grade. You got 92% and 70% of your assignments, worth 20% each and you scored 80 on your final exam which is worth 30%.

1. Enter the data:

weights <- c(0.3, 0.2, 0.2, 0.3)
grades <- c(88, 92, 70, 80)

Note: make sure you keep the same order when entering the grades and entering their associated weights. You can decide on the order, but use the same one for both variables. Here I used: midterm, assignment, assignment, final exam.

2. Find the weighted mean:

w.mean <- weighted.mean(grades,weights)

82.8

While not necessary for this question, we could also visualize and store this information in a data frame to keep track of how the grades and weights are paired. The function "data.frame" will make a table of these values which can be referenced again and extracted from as a dataset (e.g. by using the $ sign and [[ ]]); this function can be very helpful to keep track of information and compile datasets.

grades.data <- data.frame(weights, grades)

Make sure you run grades.data and note what it looks like. What has this function done?

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Measures of Variation

Exercise 5
Below is the age of the members of two groups.
Group 1: 14, 16, 19, 26, 25, 15, 17, 18, 19, 21
Group 2: 86, 79, 84, 79, 80, 82, 82, 86, 85, 83
Which group is more variable?

1. Enter the data:

G1 <- c(14, 16, 19, 26, 25, 15, 17, 18, 19, 21)
G2 <- c(86, 79, 84, 79, 80, 82, 82, 86, 85, 83)

2. Compare variances and standard deviations

Variance

var(G1)
var(G2)

Standard Deviation

sd(G1)
sd(G2)

G1 has the highest standard deviation (and variance), it is therefore the most variable of the two groups.

3. You could also use the coefficient of variation:

Coefficient of Variation

CVar.G1 <- sd(G1)/mean(G1);CVar.G1
CVar.G2 <- sd(G2)/mean(G2);CVar.G2

The answer is consistent.

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Additional information/practice questions

Skewness

Look at the frequency distribution:
1. Identify range of data:

range(Height)

121 200
2. The range is 121-200. Let's break the spread into classes of 10. To do so, let's use the range 120-210.

breaks <- seq(120,210,by=10)

The command 'breaks' creates the intervals/bins that we will use to organize the data in the next step.
You should now see in the Environment, under 'Values" a value called 'breaks' that has 'num [1:10] 120 130 140 ...' associated to it.
3. Create a frequency count:

Height.freq <- table(cut(Height,breaks,right="FALSE"))

The command 'cut' divides the range of 'Height' into the breaks that we defined previously. It also assign the values in 'Height' according to which bin they fall in. The command 'table' builds a contingency table of the counts at each break (created using the 'breaks' command).
You can use the 'Help' tab to learn more about these functions.
You should now see in the Environment, under 'Values" a value called 'Height.freq' that has ' 'table' int [1:9(1d)] 6 9 19 ...' associated to it.
4. Visual inspection:

barplot(Height.freq,main="plot")

You should see a plot called 'plot' in the Plots tab. We can see that the data is positively skewed (to the right).

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Additional information: Discrete Probability Distributions

Exercise 8
Statistics Canada reports that French is the mother tongue of 22% of Canadians. If 50 Canadians are randomly surveyed, find the probability that at most 15 have French as their mother tongue.
The following command tells us the probability of getting X successes on 50 trials when the probability of success on any individual trial is 0.22:
'dbinom(X,size=50,prob=0.22)'
If we wanted to know the probability of getting exactly 15 successes from 50 trials, we would use:

dbinom(15, 50, 0.22)

0.0515
However, we want the probability of getting no more than 15 successes. For this, use the cumulative probability function for a binomial distribution:

pbinom(15, 50, 0.22)

0.9335
If we wanted to know the probability of getting more than 15 successes, we would use the following command:

1-pbinom(15, 50, 0.22)

0.0665

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Binomial Distribution Graph

Exercise 9
You bought a pack of five cookies. Construct a binomial distribution graph for the number of broken cookies, knowing that the p=0.4.

1. Create the variable 'x = 0, 1, 2, 3, 4, 5' (the number of cookies that could be broken):

x <- seq(0,5,by=1)

2. Create the variable 'y' as the discrete binomial distribution corresponding to the x value:

y <- dbinom(x, 5, 0.4)

Do you understand what 'y' represents?

3. Construct a binomial distribution graph

plot(x,y,type="h")

Note: the argument 'type' indicates what type of plot should be drawn. Here, we choose 'h' for 'histogram'.

4. Do the same steps again using a different p. What do you observe?

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Practice questions

During the winter, flights are frequently cancelled in the city of Lethbridge, Alberta due to bad weather. The table below reports the number flights cancelled per day and their probability.

X	0	1	2	3	4	5	6	7
P(X)	0.25	0.1	0.12	0.18	0.1	0.1	0.1	0.05

1. Enter the data:
Number of flights cancelled per day

flights.canc <- c(0,1,2,3,4,5,6,7)

Probability of number of flights cancellations

prob <- c(0.25,0.1,0.12,0.18,0.1,0.1,0.1,0.05)

You should see in the Environment that a value was created for each ('flights.canc' and 'prob') under 'Values'.

2. Create a matrix and name it 'a'

a <- data.frame(flights.canc,prob)

You should see in the Environment that a data frame called 'a' was created under 'Data'. To view the data frame

Notice that you can now call upon the various columns of the matrix using the '$' sign, or any other method described the Extracting Variables section.

a$flights.canc

(a) What is the mean, the variance and the standard deviation for the number of flights cancelled in Lethbridge during winter.

mean.flights.canc <- sum(a$flights.canc*a$prob)

You should see in the Environment that a value called 'mean.flights.canc' was created under 'Values' and that the value 2.73 is associated to it. This is the mean we were looking for.

var.flights.canc <- sum(a$flights.canc^2*a$prob)-mean.flights.canc^2

You should see in the Environment that a value called 'var.flights.canc' was created under 'Values' and that the value 4.8971 is associated to it. This is the variance we were looking for.

sd.flights.canc <- sqrt(var.flights.canc)

You should see in the Environment that a value called 'sd.flights.canc' was created under 'Values' and that the value 2.2129 is associated to it. This is the standard deviation we were looking for.

(b) What is the probability that more than 4 flights are cancelled on a given day?
Answer: because there are only three possibilities in which the number of daily flight cancellation exceeds 4/day, it can be faster to answer this question using brute force:

prob.more.than.4.brute.force <- 0.1+0.1+0.05

Using a method for calculating probabilities for large sets using a for loop:

y<-NULL
for(i in seq(along=1:length(a$prob))) {y[i]<-c(if(a$flights.canc[i]>4) a$prob[i] else 0)}
prob.more.than.4 <- sum(y)

Both ways should give you the same answer: 0.25. This means 25%.
If you want to know more about for loops go here

You can also try using an ifelse conditional statement:

z<-ifelse(a$flights.canc>4,a$prob,0)

If you want to know more about ifelse conditional statements go here

MoneySense reports that the chances of winning the 'multi-million jackpots' are about 1 in 14 million for the national lottery Lotto 6/49. If someone buys 1,000,000 tickets of Lotto 6/49, what are his/her chances of winning a 'multi-million jackpot'...

prob.w <- 1/14000000
n <- 1000000
lambda.w <- prob.w*n

... zero times?

dpois(0,lambda.w)

0.9311
... once?

dpois(1,lambda.w)

0.0665
... twice?

dpois(2,lambda.w)

0.0024
... three times or more?

1-ppois(2,lambda.w)

5.757588e-05. This is scientific notation and should be read as: 0.00005757588. Once rounded to the fourth decimal: 0.0001

Remember to clear your Environment and save your R script in between exercises.

WEEK 7: Subsetting and Data Management

There are many ways to organize, manage, and work with data in R. One common way to organize and manage your data is by subsetting it. Subsetting your data is basically the process of taking a portion of your dataset based on certain criteria. For instance, the way we cleaned the allcountries dataset earlier in tutorials (all<-allcountries[complete.cases(allcountries),]) is a way of subsetting so that only rows containing complete information are included in the new, subsetted dataset.

There are a few different ways to do this with data; however, one of them is to use the subset function as follows:

object.name <- subset(dataset.name, specification.of.data.segment)

These specifications can be numeric parameters or character strings, and there are a number of ways to specify this in R.

Subsetting with categorical data

For instance, if we are using the Student Survey dataset and only want to look at the GPA of students who are in their first year, we could do the following:

Clean the dataset:

students <- StudentSurvey[complete.cases(StudentSurvey), ]

2. Subset the dataset to only include first year students:

first.year <- subset(students, Year == "FirstYear")

Here, first.year will be the name of the new subsetted dataset, students is the name of the old dataset, Year is the name of the column/variable that a specification is being made about, and "FirstYear" is the type of response in that column that we are asking R to only include in the new dataset. Alternatively, you could specify the variable or column name by extracting it from the dataset as we have done before, such as:

first.year <- subset(students, students$Year == "FirstYear")

or with the dataset and column number:

first.year <- subset(students, students[[1]] == "FirstYear")

3. Extract the variable GPA from the new dataset that only includes first year students:

GPA.first.year <- first.year$GPA

We could also choose to include all students who are not in their first year by using the != instead of the double equal sign. By placing an exclamation point in front of the equal sign, this indicates to R that we are looking for something not equal ( ≠ ) to the information we are giving R. For instance, we could use this to look at all students who are not in their first year as follows:

not.first.year <- subset(students, Year != "FirstYear")

Subsetting with numeric data

Alternatively, we can also subset data based on numeric data. For instance, if we only wanted to look at survey respondents who have siblings, we could specify this in our subset. This specification would result in a dataset that only includes rows with survey respondents who have one or more siblings. This could be done as follows:

siblings <- subset(students, Siblings >= 1)

Or, we could also write this as:

siblings <- subset(students, Siblings > 0)

Subsetting with multiple factors

We can also make subsets that include multiple specifications. For instance, if we wanted to look at students who are in their first year and who have more than one sibling we could use the ampersand key, &, to tell R that we want it to consider both of these factors in the subsetted dataset. For instance:

first.y.sib <- subset(students, Year == "FirstYear" & Siblings > 1)

If you wanted to include data that was one or the other, for instance if you wanted to look at data for students who were in their third (junior) and fourth (senior) years, you could use a vertical bar, |, to indicate to R that you want to include data in this subset that matches either of these specifications. For instance:

upper.years <- subset(students, Year == "Senior" | Year == "Junior")

Along these lines, some helpful signs to know while subsetting are:

== which means =

!= which is equivalent to ≠

>= or <= which is read as ≥ or ≤

| which can be read as "OR"

& which means "AND"

WEEK 8 & 9: The Normal Distribution

Normal Distribution (pnorm & qnorm)

To do these exercises, you will want to use the two following commands:

qnorm() function, which reports the quantile associated with a user-defined probability of getting a value less than or equal to it. For example, when a variable has a normal distribution with a mean of 80 and a standard deviation of 12, the quantile (value) associated with the probability of getting a value less than or equal to 0.9 is given by:

qnorm(0.9,80,12)

The answer is 95.37862, which means that the probability of drawing a value of 95.34 or less from this normal distribution is 90%.
Note: The default mean and sd are 0 and 1 respectively. If you don't specify a mean or a sd, R will use the default ones.

pnorm() function, which reports the area under the curve to the left of a user-defined value q (the cumulative density function). More accurately, pnorm(q,mean,sd) tells you the probability of obtaining a draw from a normal distribution (with a given mean and standard deviation) with value less than or equal to q. For example, when a variable has a normal distribution with a mean of 80 and a standard deviation of 12, the area to the left of a q-value of 90 is given by

pnorm(90,80,12)

The answer is 0.7976716, which means that the probability of drawing a value of 90 or less from this normal distribution is 79.77%.
The default mean and sd are 0 and 1 respectively. If you don't specify a mean or a sd, R will use the default ones.

To wrap-up:
pnorm() --> you enter a quantile (value), you get a probability
qnorm() --> you enter a probability, you get a quantile (value)

Exercise 10
Find z₀ such that P(z > z₀) = 0.321.
Note: Drawing (by hand) a z distribution would help you visualize this.

qnorm(0.321, lower.tail = FALSE)

0.465, which means that the probability of drawing a value of 0.465 or more from this normal distribution is 32.1%.
Note: the argument 'lower.tail' is set as 'TRUE' by default, and that means that the probabilities that we will get are P[X < x]. If we are interested in the other side, P[X > x], then we should set the argument = FALSE, like we did here.

Exercise 11
Find z₀ such that P(-2.2< z < z0) = 0.5678.
Which means: P(-2.2< z < z₀) = P(z < z₀) - P(z < -2.2) = 0.5678.
Note: Drawing (by hand) a z distribution would help you visualize this.

Let x = P(z < z₀) = 0.5678 + P(z < -2.2)

x <- 0.5678+pnorm(-2.2); x
z₀<- qnorm(x); z0

0.2062532

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Exercise 12
Download the dataset named 'All Countries' from the textbook 'Statistics: Unlocking the Power of Data, Lock.' here (choose the .rda version):
http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true.

a)Check for normality for the variable 'Life Expectancy'.

1. Upload the data:
Import a Dataset (RDA format)
2. Get rid of the observations with missing values

all <- AllCountries[complete.cases(AllCountries),]

3. Symmetry is an important feature of a normal distribution. It is a necessary (but not sufficient) condition for the data to be distributed according to a normal distribution.Visually inspect whether the data exhibit symmetry by creating an histogram.

hist(all[[14]])

We can see that the data is negatively or left-skewed.
4. Alternatively, we could have compared the median and the mean (instead of plotting an histogram).

Normal distribution: median = mean
Negatively skewed or left-skewed distribution: median > mean
Positively skewed or right-skewed distribution: median < mean

median(all[[14]])

73

mean(all[[14]])

72.43247

median (all[[14]]) > mean (all[[14]])

TRUE

b) Using the same dataset, subset the data to check for normality for the variable 'Life Expectancy' only for low rural countries (<50).

1. Create a new data set containing only low rural countries.

low.rural<-subset(all, all$Rural<50)

Your new dataset should appear on the environment. What differences do you notice between the dataset "all" and the "low.rural" dataset?

2. Check for symmetry through a histogram.

hist(low.rural[[14]])

3. Compare the median and the mean.

median(low.rural[[14]])

mean(low.rural[[14]])

median (low.rural[[14]]) > mean (low.rural[[14]])

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Applications of the Normal Distribution

Exercise 13
During the reading week, UBC Faculty members exercised for 96 minutes, on average. If we assume that the time spent exercising during reading week is normally distributed and has a standard deviation of 22.2 minutes, what is the probability that a randomly selected faculty member spent more than 90 minutes exercising during the reading break? Less than 60 minutes?

1. Enter the parameters:

Xbar <- 96
sigma <- 22.2

2. P(X > 90)=?

pnorm(90,Xbar,sigma,lower.tail = FALSE)

0.6065
Note: the argument 'lower.tail' is set as 'TRUE' by default, and that means that the probabilities that we will get are P[X < x]. If we are interested in the other side, P[X > x], then we should set the argument = FALSE, like we did here.

3. P(X < 60)=?

pnorm(60,Xbar,sigma)

0.0524

We are now interested in finding out the range of hours that the middle 40% members spent exercising during the reading break.

4. Find P(middle 40%) = P(between 30% and 70%)

max.hours <- qnorm(0.7,96,22.2);max.hours

107.6417

min.hours <- qnorm(0.3,96,22.2);min.hours

84.35831

Remember to clear your Environment and your Plots and to save your R script in between exercises.

The Central Limit Theorem

Exercise 14
The midterm average for a given class is 76.8% and the standard deviation is 13.1%. Assume the variable is normally distributed.

1. Enter the parameters:

mu <- 76.8
sigma <- 13.1

2. If a student from the class is randomly selected, find the probability that her average will be between 79 and 82%.
Find P(79 < X < 82) = P(X < 82) - P(X < 79)

pnorm(82,mu,sigma) - pnorm(79,mu,sigma)

3. If a random sample of 15 students is selected, find the probability that the mean grade of this sample will be between 79 and 82%.
Find P(79 < Xbar < 82) = P(Xbar < 82) - P(Xbar < 79)

mu <- 76.8
sd <- 13.1/sqrt(15)

Note the division of the sample's standard deviation by the sample size!

pnorm(82,mu,sd)-pnorm(79,mu,sd)

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Additional information/practice questions

Normal approximation to Binomial Distribution

Gartner reports that Samsung had 26.2% of the market share of worldwide smartphone sales to end-users by vendor in 2014. If 200 users who bought smartphones in 2014 are selected at random, find the probability that fewer than 50 bought a Samsung.
Identify parameters

p.sam <- 0.262
n <- 200

You should now see values for both in the Environment.

Use the logical operator ">=" to check whether p.sam x n and (1-p.sam) x n are both greater than 5 (in which case, using a normal approximation is reasonable):

p.sam*n>=5
(1-p.sam)*n>=5

The answer will appear in the console. It should be 'TRUE' for both.
Since p*n >=5 and q*n>=5, proceed to find the approximate probability.
Calculate mean and standard deviation:

mu <- p.sam*n
sigma <- sqrt(p.sam*n*(1-p.sam))

Apply continuity correction: P_binomial(X<50,p=0.262) is approximately equal to P_normal(X<49.5,mean=mu,sd=sigma)

pnorm(49.5,mean=mu,sd=sigma)

Answer=0.3204855

Remember to clear your Environment and Plots and save your R script in between exercises.

WEEK 10: Confidence Intervals & Hypothesis Testing

Confidence Intervals for the Mean (when sigma is known) & Z Test for the Mean

To use the R command to get the z test for the mean, we need to install the "TeachingDemos" package and its library.
1. Run the following command:

install.packages("BSDA")

2. Click 'yes' on the pop-up windows.
3. Run the following command:

library(BSDA)

Exercise 15
A paper reports that on average, students spend 100 hours deciding which masters programs they will apply to. One university does not believe this result and decides on surveying 49 graduate students about their experience. The results are reported below.
122 130 127 112 111 87 115 92 107 106 94 129
134 113 109 82 100 95 80 113
121 96 125 110 98 114 85 104 109 92
80 96 97 105 90 113 82 79 106 115 128 122 89 97 107 116 91 131
112
Assume sigma of 17 hours.

At alpha = 0.05, can the statement be disproved?

1. Enter the data:

hours <- scan ()
122 130 127 112 111 87 115 92 107 106 94 129
134 113 109 82 100 95 80 113 
121 96 125 110 98 114 85 104 109 92 
80 96 97 105 90 113 82 79 106 115 128 122 89 97 107 116 91 131 
112

Note: it is important to have a blank line at the end of the data, to let R know that there is no more data to be scanned. You will have to manually enter that blank line by pressing 'Enter' after having placed your cursor in the console.

2. State hypothesis and identify claim:
H0: mu is equal to 100
H1: mu is unequal to 100 (claim)

3. Z test:

z.test(hours,mu=100, sigma.x=17, alternative="two.sided")

Results (you should see the following printed in your console):
One-sample z-Test
data: hours
z = 2.2521, p-value = 0.02432
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
100.7095 110.2293
sample estimates:
mean of x
105.4694

4. Summarize the result:
There is enough evidence to reject the Ho that on average students spend 100 hours deciding which masters programs they will apply to, at 95% confidence level.

5. What about at alpha = 0.01?

z.test(hours,mu=100, sigma.x=17, alternative="two.sided", conf.level = 0.99)

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Exercise 16
The students in LFS252 have different numbers of followers on Twitter. Below are the numbers of followers for 30 students of that class that were randomly selected:
30 120 46 106 130 19 59
80 76 11 19 99 234 36 20 79 240
180
140 78 67 87 123 65 89 34 109
77 117 157
Find the 92% confidence interval of the population (all the LFS252 students) mean for the number of Twitter followers.
A prior study indicated that sigma=55

1. Enter the data:

followers <- scan()
30 120 46 106 130 19 59
80 76 11 19 99 234 36 20 79 240
180
140 78 67 87 123 65 89 34 109
77 117 157

Note: it is important to have a blank line at the end of the data, to let R know that there is no more data to be scanned. You will have to manually enter that blank line by pressing 'Enter' after having placed your cursor in the console.

2.Using z test to find the 92% confidence interval:

z.test(followers,sigma.x=55,alternative="two.sided",conf.level = 0.92)

Note: When finding a confidence interval, we don't need to identify the argument "mu", as we are not testing the true mean (mu). The default value will be 0.

3. Conclude:
We are 92% confident that the population mean of twitter followers is between 73.32 and 108.48, based on a sample of 30 students.

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Confidence Intervals for the Mean (when sigma is unknown) & T Test for the Mean

Exercise 17
A city thinks that bike commuters bike for 110 minutes weekly, on average. To test that, the city randomly selected 56 bike commuters and asked them about their commuting time. At alpha=0.05 can we conclude that the average of weekly bike commute is still 110 minutes?
Download the dataset 'BikeCommute' from the textbook 'Statistics: Unlocking the Power of Data, Lock.' here: http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true.

1. Import the dataset, extract the variable of interest ('Minutes') and name it 'bike.minutes':

You know how to do that!

2. State the hypothesis and identify the claim:

H0: mu is equal to 110. (claim)
H1: mu is unequal to 110.

3. Using t.test

t.test(bike.minutes,mu=110,alternative="two.sided",conf.level = 0.95)

Result (you should see that in the console):
One Sample t-test
data: bike.minutes
t = -2.6577, df = 55, p-value = 0.01028
alternative hypothesis: true mean is not equal to 110
95 percent confidence interval:
106.5727 109.5194
sample estimates:
mean of x
108.0461

4. Conclude:
P-value=0.01028 < alpha=0.05, reject H0.
There is not enough evidence to support the claim that the average is 110 minutes per week.

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Exercise 18
20 randomly selected students were surveyed about how many hours they studied for their LFS252 midterm exam. Here are their answers:
10, 50, 45, 2, 15, 12, 20, 22, 25, 31, 33, 47, 33, 22, 24, 100, 40, 42, 45, 44
Find the 95% confidence interval for the average number of hours spent studying by all LFS252 students.

1. Enter the data:

hours_2 <- c(10, 50, 45, 2, 15, 12, 20, 22, 25, 31, 33, 47, 33, 22, 24, 100, 40, 42, 45, 44)

2. Using t.test.

t.test(hours_2,alternative="two.sided",conf.level = 0.95)

Note: you see why we do not need to identify the argument 'mu' here?

3. Conclude:
We are 95% confident that the population mean hours spent studying for the midterm by all the LFS252 students is between 23.30 and 42.90 hours, based on 20 randomly selected students.

Remember to clear your Environment and your Plots and to save your R script in between exercises.

Review exercises and useful information

Exercise 1

In a given city, a survey was performed on 100 randomly selected adults (age range 20-80 years; 50 females, 50 males). The data obtained per subject were: hourly wages (CAD; "Salary"), gender (female = 0, male = 1; "Gender"), age (years; "Age"), and PhD degree ( no = 0, yes = 1; "PhD").

1. Download the dataset 'SalaryGender' from the textbook 'Statistics: Unlocking the Power of Data, Lock.' here: http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true.

2. Inspect your dataset.

Go to your Environment, and find the dataset under Data. How many observations (rows) and variables (columns) does your dataset has?
Click on the dataset to view it.

 names(SalaryGender)

3. To estimate the mean and standard deviation of the salary per gender, type:

 tapply(SalaryGender$Salary, SalaryGender$Gender, mean); tapply(SalaryGender$Salary, SalaryGender$Gender, sd)

Note: remember that the semicolon states the end of one command land the start of another (that could be written in different command lines).

Now try to estimate the mean and standard deviation for people with or without a PhD degree:

 tapply(SalaryGender$Salary, SalaryGender$PhD, mean); tapply(SalaryGender$Salary, SalaryGender$PhD, sd)

Note: 0 states for subjects without and 1 for subjects with PhD degree.

4. Visually assess symmetry of the variable "Age"

hist(SalaryGender$Age)

Remember to clear your Environment and Plots and save your R script in between exercises.

Exercise 2
Try to do exercise 10, page 414, in Triola 5th edition.
Note: to download the dataset, access mystatlab, go to "chapter contents" on the left, click appendix B, multimedia eText, go to page 610 and click SC. By clicking SC you will open the dataset, now save it by going into "data", then "export". A new window will open, click export and save the CSV file in the folder of your preference.

Exercise 3
Try to do exercise 12, page 415, in Triola 5th edition.

Remember to clear your Environment and Plots and save your R script in between exercises.

WEEK 11:Hypothesis Testing (t tests): Comparing the means of two independent samples. One-way Analysis of Variance

t.test comparing of two independent samples

Effect of maternal style in the adult responses to stress in the laboratory rat
A group of researchers was interested in testing if rats reared by highly invested mothers (mothers that groom more and respond to pup´s calls more often), as adults were less responsive to stress (measured in plasma corticosterone), than adult rats reared with low invested mothers. Researchers randomly selected and marked 15 pups from highly invested mothers (one pup from each of 15 litters), and 15 pups from low invested mothers (one pup from each of 15 litters).
At 3 months of age, rats were subjected to a social challenge and plasma corticosterone levels (µg/dL) were measured. Perform a t.test with a significance level of 0.05.
Results obtained are presented in Table 1.
Table 1.

'RatID	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
'treatment	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
stress_resp	8.47	8.59	7.01	7.80	7.37	9.37	0.52	11.04	8.20	9.99	12.66	10.74	10.55	10.94	9.59	52.52	50.28	50.52	49.62	47.38	50.03	50.27	46.21	49.83	49.67	50.71	51.78	52.24	49.22	47.40

Import the data

stress_resp<-scan()
8.47  8.59  7.01  7.80  7.37  9.37 10.52 11.04  8.20  9.99 12.66
10.74 10.55 10.94  9.59 52.52 50.28 50.52 49.62 47.38 50.03 50.27
46.21 49.83 49.67 50.71 51.78 52.24 49.22 47.40
RatID<-seq(1,30,by=1)
treatment<-c(rep(0,15),rep(1,15))

Function rep gives you the first argument repeated as many times stated in the second argument. Here we used function c to combine both series of repetitions.
Create a dataset

mat_style<-data.frame(RatID,treatment,stress_resp)

State that treatment is a factor where 0= highly invested mom and 1= low invested mom, with function factor.

mat_style$treatment<-factor(mat_style$treatment)

Do you want to save your dataset as CSV?

write.csv(mat_style, "C:/Users/Hp/Desktop/LFS 252 2016/mat_style.csv")

Check for normality using a Shapiro-Wilk test of normality. We state a null hypothesis, H0: the data is normally distributed, and Ha: the data is not normally distributed. If p<0.05, then we have evidence to reject H0, and we state that our distribution is different than the normal distribution.

shapiro.test(mat_style$stress_resp[mat_style$treatment==0])
shapiro.test(mat_style$stress_resp[mat_style$treatment==1])

See how first we state the function, then within the parenthesis we state that we want to run the test in the variable stress_resp from the dataset mat_style, only for the highly invested moms( i.e. when mat_style$treatment==0). This is another way of subseting!

Create a simple plot to visualize the results

plot(mat_style$stress_resp~mat_style$treatment)

Now let’s perform the test to look at the differences between to independent samples means (t.test for two means)

t.test(stress_resp~treatment,data=mat_style,alternative = "two.sided")

If our samples were paired (not independent), we add another argument to the function t.test, after data, we ad paired=TRUE.

Remember to clear your Environment and your Plots and to save your R script in between exercises.

One-way Analysis of Variance

As a follow up study, researchers now want to add another treatment to the same experimental design. The third treatment is: rats reared in isolation. For this study, researchers followed the same protocol, but selected an extra sample of 15 rats, and reared them in isolation.
Results obtained are presented in Table 2.
Table 2. Part1

'RatID	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
'treatment	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1
stress_resp.2	8.45	13.85	13.95	11.66	9.06	11.60	8.14	8.68	13.38	7.63	12.67	13.37	9.50	11.85	10.03	43.43	53.64	50.39	49.17	49.80	49.01	46.01

Table 2. Part2

'RatID	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45
'treatment	1	1	1	1	1	1	1	1	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2
stress_resp.2	48.63	48.61	50.22	50.99	55.03	48.22	51.86	44.49	63.80	62.77	67.64	56.57	51.21	51.81	57.19	59.77	64.29	57.31	61.51	59.71	61.23	59.90	55.28

Import the data.

stress_resp.2<-scan()
8.45 13.85 13.95 11.66  9.06 11.60  8.14  8.68 13.38  7.63 12.67
13.37  9.50 11.85 10.03 43.43 53.64 50.39 49.17 49.80 49.01 46.01
48.63 48.61 50.22 50.99 55.03 48.22 51.86 44.49 63.80 62.77 67.64
56.57 51.21 51.81 57.19 59.77 64.29 57.31 61.51 59.71 61.23 59.90
55.28
RatID<-seq(1,45,by=1)
treatment<-c(rep(0,15),rep(1,15),rep(2,15))

Create a dataset.

mat_style.2<-data.frame(RatID,treatment,stress_resp.2)

State that treatment is a factor.

mat_style.2$treatment<-factor(mat_style.2$treatment)

Save your dataset.

write.csv(mat_style.2, "C:/Users/Hp/Desktop/LFS 252 2016/mat_style2.csv")

Check for normality of the data.

shapiro.test(mat_style.2$stress_resp.2[mat_style.2$treatment==0])
shapiro.test(mat_style.2$stress_resp.2[mat_style.2$treatment==1])
shapiro.test(mat_style.2$stress_resp.2[mat_style.2$treatment==2])

To investigate if there are differences between the thee means, we fit a one-way ANOVA model using the lm function. We save the model fitted in an object to be able to use and extract different elements from the model. Then, to obtain the analysis of variance from this model, we use de function anova.

m1<-lm(mat_style.2$stress_resp.2~mat_style.2$treatment);anova(m1)

or

m2<-aov(mat_style.2$stress_resp.2~mat_style.2$treatment); summary(m2)

You will get the Analysis of Variance Table as follows. Do you understand what you see?

Response: mat_style.2$stress_resp.2
Df Sum Sq Mean Sq F value Pr(>F)
treatment 1 17577.4 17577.4 301.96 < 2.2e-16 ***
Residuals 43 2503.1 58.2
--- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Now make a simple plot to visualize your results

 plot(mat_style.2$stress_resp.2~mat_style.2$treatment)

To get the mean and standard deviation per treatment write the following commands:

 tapply(mat_style.2$stress_resp.2,mat_style.2$treatment,mean)
 tapply(mat_style.2$stress_resp.2,mat_style.2$treatment,sd)

Linear regression

Linear regression can be a powerful and helpful tool to assess relationships between different variables. It is important to note that there are a number of assumptions about one’s data and the relationships between different variables made when using linear regression as a tool for statistical analysis, including: that the relationship between the variables is linear; normality of residuals; constant variance that is randomly distributed (homoscedasticity); and error independence.

This section is focused on the code used to assess this data in R, providing that these assumptions are met. If these assumptions are met, the basic code to create a linear model in R is:

lm(dependent.variable.y ~ independent.variable.x)

This code might look similar as we used it to create a line of best fit earlier for a scatter plot with the abline( ) function. However, if we want to learn more about the details of this linear relationship, we could use the summary( ) function as follows:

summary(lm(dependent.variable.y ~ independent.variable.x))

For example, we could use the student survey dataset (from the following link: http://bcs.wiley.com/he-bcs/Books?action=mininav&bcsId=8088&itemId=0470601876&assetId=322396&resourceId=31651&newwindow=true) to look at the relationship between student weights (y) as they change with student heights (x). Assuming that the assumptions above have been met, we could proceed with the following:

Check your data and ensure it is clean. One way of doing this is by subsetting using the complete.cases( ) function:

	students <- StudentSurvey[complete.cases(StudentSurvey),]

Make a scatter plot to visualize the relationship between our data (note: this step is optional, but highly recommended)

	plot(students$Height, students$Weight)

	abline(lm(students$Weight ~ students$Height), col = "magenta")

Make a linear model of the relationship between the data points and summarize it:

	model <- lm(students$Weight ~ students$Height)

	summary(model)

Your output should look like the following:

Linear regression output in R

Do you know how to interpret this? A key is below to check your work against:

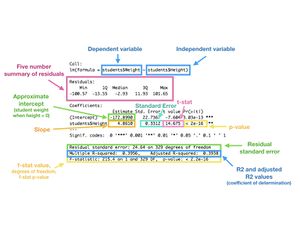
Labelled linear regression output in R

There are many resources online that can help to expand on these functions and posts. A couple links that might help you get started are listed below.

Interpreting the output: https://feliperego.github.io/blog/2015/10/23/Interpreting-Model-Output-In-R

Assessing linear regression assumptions: http://r-statistics.co/Assumptions-of-Linear-Regression.html

We hope you have found this introduction to R helpful! :)

Remember to clear your Environment and your Plots and to save your R script in between exercises.